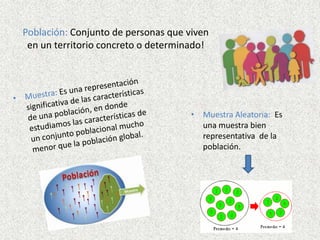
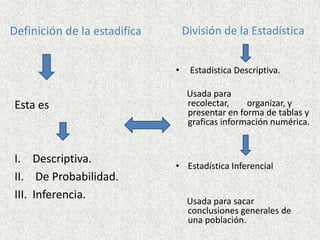
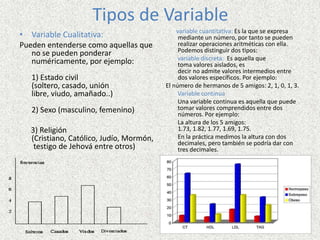
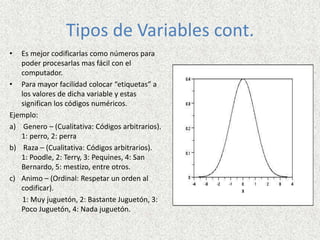
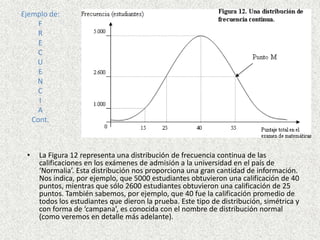
Este documento presenta definiciones clave de conceptos estadísticos como población, muestra, variable, dato, parámetro, estadístico, encuesta, censo y tipos de variables. También describe técnicas de muestreo como muestreo aleatorio, estratificado, conglomerados y sistemático. Además, explica conceptos como tabla de frecuencias, frecuencia relativa, frecuencia absoluta y frecuencia acumulada. Por último, provee un ejemplo de distribución de frecuencias continua.

1. Universidad Fermín Toro
Vicerectorado Académico
Facultad de Ciencias Sociales
Escuela de Comunicación Social
CONCEPTOS BASICOS
Jesús Herrera
V-24.400.569
Estadística
M-742

2. Población: Conjunto de personas que viven
en un territorio concreto o determinado!
• Muestra Aleatoria: Es
una muestra bien
representativa de la
población.

3. Variable: Es una estructura
de datos, que puede
cambiar su valor según la
situación deseada
• Dato: Un dato es
un documento, una infor
mación o
un testimonio que
permite llegar al
conocimiento de los
hechos.
Parámetro: Es un número que
resume la ingente cantidad
de datos que pueden
derivarse del estudio de
una variable estadística.

4. Estadístico: Un estadístico
(muestral) es una medida
cuantitativa, derivada de un
conjunto de datos de
una muestra, con el objetivo de
estimar o inferir características
de una población o
modelo estadístico.
Encuesta: Un conjunto de
preguntas normalizadas
dirigidas a una muestra
representativa de la población
o instituciones, con el fin de
conocer estados de opinión o
hechos específicos.
• Censo: Se entiende por censo
aquella numeración que se
efectúa a todos y cada uno
de los caracteres
componentes de una
población.
•

5. Definición de la estadifica División de la Estadística
• Estadística Inferencial
Usada para sacar
conclusiones generales de
una población.
Esta es
I. Descriptiva.
II. De Probabilidad.
III. Inferencia.
• Estadística Descriptiva.
Usada para
recolectar, organizar, y
presentar en forma de tablas y
graficas información numérica.

6. De acuerdo a la Grafica del Análisis
Estadístico:
– Lo que respecta a mi opinión no se trata mas que de un
ciclo de como funciona la estadística, por ende se llama
Análisis Estadístico ya que este nos proporciona una
capacidad para comparar de población a muestra, de
muestra a muestra estadístico (estadística inferencial), de
muestra estadístico a estadística tanto inferencial como
probabilidad y es ahí de donde sacamos el resultado de lo
que se esta tratando de encontrar un resultado.
Ejemplo:

7. Pasos de un estudio estadístico
• Plantear Hipótesis sobre una
población:
“Estudiante trabajador tiene menos
tiempo de descansar que el no
trabajador”
¿Porque? ¿Cuanto descansa el uno y el otro?
¿Qué tipo de estudio obtiene cada uno?
¿Cuál tiene mayor animo?
• Decidir que datos recoger:
Que individuo pertenecen al estudio.
a) trabajador y no trabajador en el ámbito
estudiantil.
b) Criterio de exclusión: ¿Cómo lo
elegimos?, ¿Se descarta el que no
estudia?
Pasos de un estudio estadístico
cont.
• Recoger los datos
De que forma recolecto la
información
• Describir los datos obtenidos
1- Tiempo medio de descanso de los
trabajadores y no trabajadores
2- Que por % de descanso por trabajo y
tiempo?.
• Realizar una Inferencia de la
población
Los no trabajadores tienen mas
tiempo de realizar sus actividades de
gusto que los trabajadores.
• Cuantificar la confianza en la
inferencia
Nivel de confianza en si mismos: 95%
Significación del contraste: valor = 2% ¿?

8. Técnicas de Muestreo
Muestreo aleatorio: En el que la selección de
los elementos de la muestra se hace de forma
aleatoria sin que en su composición influya
la opinión o preferencia de la persona que la
selecciona.
Ejemplo:
1) Un colegio tiene 120 alumnos de
bachillerato. Se quiere extraer una muestra de
30 alumnos. Explica como se obtiene la
muestra
a) Mediante un muestreo aleatorio simple
- Se numeran los alumnos del 1 al 120
- Se sortean 30 números de entre los 120
- La muestra estará formada por los 30
alumnos a los que les correspondan los
números obtenidos.
Muestreo Estratificado: Se usa cuando se
conoce de antemano que la población esta
dividida en estratos.
Ejemplo:
Cada estrato queda representado en la
muestra en proporción exacta a su frecuencia
en la población total.
Si el 5% de la población son estudiantes del
2do semestre, el 5% de la
muestra se extraerá de ese
estrato
N = 600 y n = 20
1er sem.: 150 alumnos (5)
2do sem.: 100 alumnos (3)
3er sem.: 200 alumnos (7)
4to sem.: 150 alumnos (5)
Cada elemento, alumnos, de cada estrato se
seleccionan utilizando el muestreo aleatorio o
al azar

9. Muestreo Conglomerados: Se utiliza
cuando los individuos de la
población constituyen grupos
naturales o conglomerados. La
unidad muestral es el
conglomerado y no los individuos
como en los anteriores.
Ejemplo:
Extraer una muestra aleatoria de los
estudiantes de las universidades
autónomas mexicanas las
universidades autónomas
mexicanas
Conglomerados: Universidades
autónomas del país Facultades o
Institutos de cada universidad
autónoma seleccionada
Carreras
Grupos o clases
Cada elemento del conglomerado se
selecciona utilizando el muestreo
aleatorio o al azar
Muestreo Sistemático: Se elige un
individuo al azar y a partir de él, a
intervalos constantes, se eligen
los demás hasta completar la
muestra
Ejemplo:
para una N = 600 y un n = 20
Se ordenan los alumnos y se
numeran, se elige uno al azar.
Ejemplo: 27 y a partir de 27 se
eligen de 30 en 30 hasta
completar la muestra.
27; 57; 87; 117; 147; 177; 207;
237; 267; 297; 327;
357; 387; 417; 447;477; 507; 537;
567; 597

10. Tipos de Variable
• Variable Cualitativa:
Pueden entenderse como aquellas que
no se pueden ponderar
numéricamente, por ejemplo:
1) Estado civil
(soltero, casado, unión
libre, viudo, amañado..)
2) Sexo (masculino, femenino)
3) Religión
(Cristiano, Católico, Judío, Mormón,
testigo de Jehová entre otros)
variable cuantitativa: Es la que se expresa
mediante un número, por tanto se pueden
realizar operaciones aritméticas con ella.
Podemos distinguir dos tipos:
variable discreta: Es aquella que
toma valores aislados, es
decir no admite valores intermedios entre
dos valores específicos. Por ejemplo:
El número de hermanos de 5 amigos: 2, 1, 0, 1, 3.
Variable continua
Una variable continua es aquella que puede
tomar valores comprendidos entre dos
números. Por ejemplo:
La altura de los 5 amigos:
1.73, 1.82, 1.77, 1.69, 1.75.
En la práctica medimos la altura con dos
decimales, pero también se podría dar con
tres decimales.

11. Tipos de Variables cont.
• Es mejor codificarlas como números para
poder procesarlas mas fácil con el
computador.
• Para mayor facilidad colocar “etiquetas” a
los valores de dicha variable y estas
significan los códigos numéricos.
Ejemplo:
a) Genero – (Cualitativa: Códigos arbitrarios).
1: perro, 2: perra
b) Raza – (Cualitativa: Códigos arbitrarios).
1: Poodle, 2: Terry, 3: Pequines, 4: San
Bernardo, 5: mestizo, entre otros.
c) Animo – (Ordinal: Respetar un orden al
codificar).
1: Muy juguetón, 2: Bastante Juguetón, 3:
Poco Juguetón, 4: Nada juguetón.

12. Ejemplo de Tipo de Variable Cont.
• Las Variables
Continuas, sería como la
medida de una tabla, (1
cm, 1.5cm, 3.58
cm, etc), ó el peso de
algo, (2.6 kg 3.7 kg), Aquí
las variables sufren
variaciones continuas, y
no se brinca de 1 a 2, la
variación es continua
porque entre el 1 y el
2, existen ifinidad de
cantidades
(1.2, 1.02, 1.0009, 1.999,
etc).
• Ejemplo de una medida
en una tabla (en la
SIGUIENTE IMAGEN).

13. Tabla de Frecuencias
Frecuencia Relativa: Por
ejemplo, si lanzas una moneda 20
veces y 14 veces cae águila en el
experimento, la frecuencia relativa
del evento águila sería 14/20 y
dicho resultado constituiría la
frecuencia relativa.
Frecuencia Absoluta: Por
ejemplo. deportes que se
practican mas frecuentes:
Futbol: 21
Básquetbol: 16.
Ese es un ejemplo de las veces
que se repiten o las personas que
practican ese deporte.
La frecuencia acumulada:
La frecuencia acumulada se
representa por Fi.
Ejemplo: Durante el mes de julio, en
una ciudad se han registrado las
siguientes temperaturas
máximas:
• 32, 31, 28, 29, 33, 32, 31, 30, 31,
31, 27, 28, 29, 30, 32, 31, 31, 30,
30, 29, 29, 30, 30, 31, 30, 31, 34,
33, 33, 29, 29
xi fi Fi
27 1 1
28 2 3
29 6 9
30 7 16
31 8 24
32 3 27
33 3 30
34 1 31
31

14. Ejemplo de:
F
R
E
C
U
E
N
C
I
A
Cont.
• La Figura 12 representa una distribución de frecuencia continua de las
calificaciones en los exámenes de admisión a la universidad en el país de
‘Normalia’. Esta distribución nos proporciona una gran cantidad de información.
Nos indica, por ejemplo, que 5000 estudiantes obtuvieron una calificación de 40
puntos, mientras que sólo 2600 estudiantes obtuvieron una calificación de 25
puntos. También sabemos, por ejemplo, que 40 fue la calificación promedio de
todos los estudiantes que dieron la prueba. Este tipo de distribución, simétrica y
con forma de ‘campana’, es conocida con el nombre de distribución normal
(como veremos en detalle más adelante).