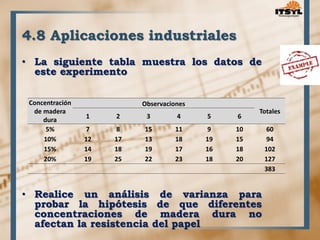
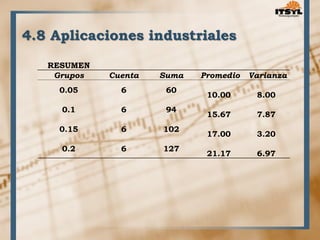
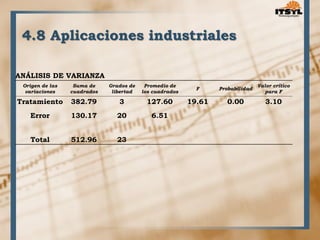
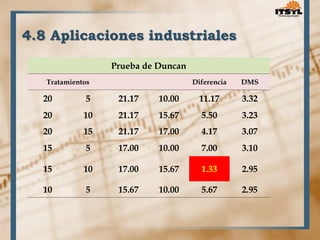
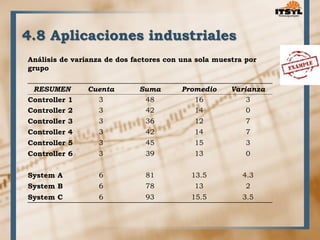
El documento describe el diseño experimental para un factor. Explica que el diseño experimental fue desarrollado por Sir Ronald Fisher en 1935 y ahora se usa ampliamente en ciencias e industrias. Define el diseño experimental como una técnica estadística para identificar y cuantificar las causas de un efecto mediante la manipulación controlada de variables. Luego describe varios diseños experimentales como el diseño completamente aleatorizado y el diseño en bloques completos aleatorizados.