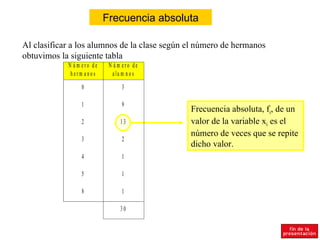
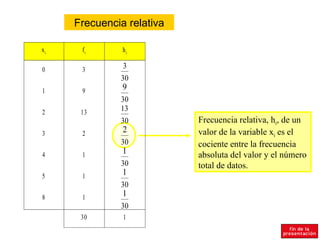
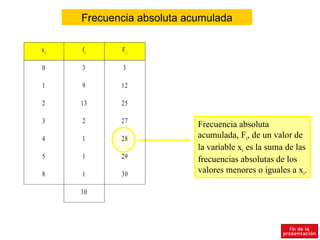
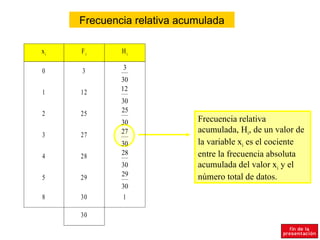
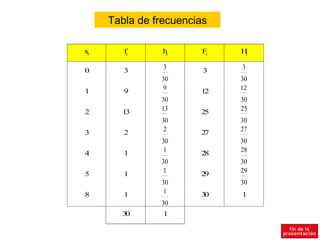
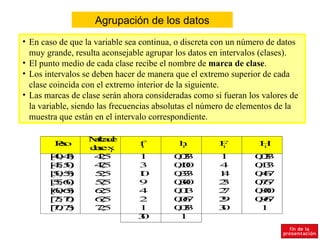
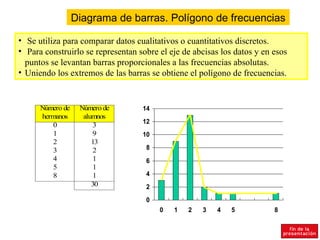
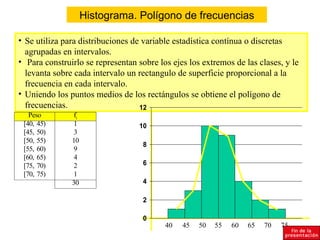
El documento resume conceptos básicos de estadística como población, muestra, variables, frecuencias absolutas y relativas, tablas de frecuencias, agrupación de datos, diagramas de sectores y barras, e histograma. Explica que la población es el conjunto total de elementos y la muestra una parte representativa de la población. Define variables cualitativas y cuantitativas, y los diferentes tipos de frecuencias para organizar y analizar los datos estadísticos.

1. X.MANUEL BESTEIRO ALONSO

2. Población y muestra
• Población: conjunto de todos los elementos que cumplen una determinada
característica.
• Muestra: cualquier parte de la población.
• Muestreo aleatorio: es aquel en el que todos los elementos de la población
tienen la misma probabilidad de ser incluidos en la muestra.
Si la muestra es elegida por un
procedimiento correcto será muy
poco probable que no sea
representativa de la población.

3. Caracteres y variables estadísticas
• Carácter estadístico es una propiedad que permite clasificar a los
individuos de una población. Puede ser cualitativo o cuantitativo.
• Variable estadística es el conjunto de valores que toma un carácter
estadístico cuantitativo. Puede ser
• discreta cuando sólo toma valores aislados;
• continua cuando toma todos los valores posibles en un intervalo.
Cualitativos Modalidades
Caracteres
Variables discretas
Cuantitativos Variables estadísticas
Variables continuas
Los valores que toma una variable estadística X se representan por {x1, x2,
x3, ... ,xn }.

4. Frecuencia absoluta
Al clasificar a los alumnos de la clase según el número de hermanos
obtuvimos la siguiente tabla
N úm ero de N úm ero de
herm anos a lu m n o s
0 3
1 9
Frecuencia absoluta, fi, de un
2 13 valor de la variable xi es el
número de veces que se repite
3 2
dicho valor.
4 1
5 1
8 1
30

5. Frecuencia relativa
xi fi hi
0 3 3
30
1 9 9
30
2 13 13
30 Frecuencia relativa, hi, de un
3 2 2 valor de la variable xi es el
30 cociente entre la frecuencia
4 1 1 absoluta del valor y el número
30 total de datos.
5 1 1
30
8 1 1
30
30 1

6. Frecuencia absoluta acumulada
xi fi Fi
0 3 3
1 9 12
2 13 25
3 2 27
Frecuencia absoluta
4 1 28 acumulada, Fi, de un valor de
la variable xi es la suma de las
5 1 29 frecuencias absolutas de los
8 1 30
valores menores o iguales a xi.
30

7. Frecuencia relativa acumulada
xi Fi Hi
0 3 3
30
12
1 12
30
2 25 25
30 Frecuencia relativa
27 acumulada, Hi, de un valor de
3 27
30 la variable xi es el cociente
4 28 28 entre la frecuencia absoluta
30 acumulada del valor xi y el
5 29 29 número total de datos.
30
8 30 1
30

8. Tabla de frecuencias
xi fi hi Fi Hi
0 3 3 3 3
30 30
1 9 9 12 12
30 30
13 25
2 13 25
30 30
3 2 2 27 27
30 30
4 1 1 28 28
30 30
5 1 1 29 29
30 30
8 1 1 30 1
30
30 1

9. Agrupación de los datos
• En caso de que la variable sea continua, o discreta con un número de datos
muy grande, resulta aconsejable agrupar los datos en intervalos (clases).
• El punto medio de cada clase recibe el nombre de marca de clase.
• Los intervalos se deben hacer de manera que el extremo superior de cada
clase coincida con el extremo interior de la siguiente.
• Las marcas de clase serán ahora consideradas como si fueran los valores de
la variable, siendo las frecuencias absolutas el número de elementos de la
muestra que están en el intervalo correspondiente.
M d
aae
rc
Po
es f
i h
i F
i H
i
cs:x
lei
a
[04
4 5
, ) 45
2, 1 03
, 3
0 1 03
, 3
0
[55
4 0
, ) 45
7, 3 00
, 0
1 4 03
, 3
1
[05
5 5
, ) 55
2, 1
0 03
, 3
3 1
4 06
, 7
4
[56
5 0
, ) 55
7, 9 00
, 0
3 2
3 06
, 7
7
[06
6 5
, ) 65
2, 4 01
, 3
0 2
7 00
, 0
9
[57
7 0
, ) 65
7, 2 06
, 7
0 2
9 06
, 7
9
[07
7 5
, ) 75
2, 1 03
, 3
0 3
0 1
3
0 1

10. Diagrama de sectores
• Se utiliza para comparar las distintas modalidades de un carácter.
• El ángulo central de cada sector ha de ser proporcional a la frecuencia
absoluta correspondiente
Ato o ía
u nm f Ág loc n l
n u e tra
i
19
Ad lu ía
na c 19 28
2º ⋅ 360º = 228º
Cs – aMn h 7
a tilla L a c a 8º
4 30
Cta ñ
a lu a 2 2º
4
Glic
a ia 1 1º
2
1
P ísVs o
a ac 1 1º
2 ⋅ 360º = 12º
30 30
Andalucía
Castilla–La Mancha
Cataluña
Galicia
País Vasco

11. Diagrama de barras. Polígono de frecuencias
• Se utiliza para comparar datos cualitativos o cuantitativos discretos.
• Para construirlo se representan sobre el eje de abcisas los datos y en esos
puntos se levantan barras proporcionales a las frecuencias absolutas.
• Uniendo los extremos de las barras se obtiene el polígono de frecuencias.
Número de Número de 14
hermanos alumnos
12
0 3
1 9 10
2 13
3 2 8
4 1 6
5 1
8 1 4
30 2
0
0 1 2 3 4 5 8

12. Histograma. Polígono de frecuencias
• Se utiliza para distribuciones de variable estadística contínua o discretas
agrupadas en intervalos.
• Para construirlo se representan sobre los ejes los extremos de las clases, y le
levanta sobre cada intervalo un rectangulo de superficie proporcional a la
frecuencia en cada intervalo.
• Uniendo los puntos medios de los rectángulos se obtiene el polígono de
frecuencias. 12
Peso fi
[40, 45) 1 10
[45, 50) 3
[50, 55) 10
8
[55, 60) 9
[60, 65) 4
[75, 70) 2 6
[70, 75) 1
30 4
2
0
40 45 50 55 60 65 70 75