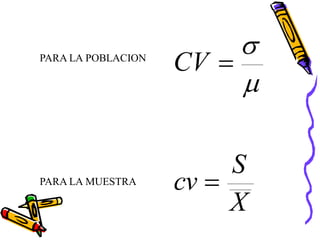
Este documento describe diferentes medidas descriptivas para condensar y describir datos, incluyendo medidas de tendencia central (media, mediana y moda), medidas de dispersión (rango, desviación típica y varianza) y medidas de asimetría y forma (sesgo, curtosis y simetría). Explica que las medidas de tendencia central proporcionan un solo valor para representar los datos centrales, mientras que las medidas de dispersión miden qué tan extendidos están los datos y las medidas de asimetría y forma describen la forma de la curva de distribución.

1. Módulo 3

2. Medidas Descriptivas
Para condensar y describir los datos se utilizan las medidas de
Tendencia central , las medidas de dispersión y las medidas de
Asimetría y forma.
A las medidas de tendencia central se les conocen así, ya que
pueden condensar en un solo valor central alrededor del cual
todos los datos se distribuyen
Variabilidad o dispersión: se refiere a la extensión de los datos de
una distribución, es decir el grado en que las observaciones se
distribuyen
Forma o Sesgo: las curvas que representan los puntos de un conjunto
de datos pueden ser sesgadas o simétricas.
En una curva simétrica una línea vertical que pase por el punto más alto de la curva divide
el área en dos partes iguales.
En una curva sesgada los valores de su distribución de frecuencias están concentrados en
el extremo inferior o en el superior de la escalad e medición horizontal

3. Medidas Descriptivas
Tendencia Central Variabilidad Forma
Y Posición
• Media • Rango • Sesgo
• Mediana • Desviación Típica • Curtosis
• Moda •Varianza • Simetría
• Cuartiles • Coeficiente de
• Deciles Variación
• Percentiles

4. Tendencia Central o de Posición
Las medidas de tendencia central son valores numéricos que
señalan un tipo de centro de un conjunto de datos, centro
que se utiliza para representar el conjunto.
Las medidas de posición facilitan información sobre la serie de
datos que se está analizando.
Estas medidas permiten conocer diversas características de
una serie de datos.

5. Las medidas de posición son de dos tipos:
•Medidas de posición central:
Informan sobre los valores medios de la serie de datos.
Son medidas que buscan posiciones (valores) con respecto a los
que los datos muestran tendencia a agruparse.
•Medidas de posición no centrales:
•Informan de como se distribuye el resto de los valores de la serie.
Permiten conocer otros puntos característicos de la distribución
que no son los valores centrales.

6. Medidas de posición central
Media
Mediana
Moda
Medidas de posición no centrales
Cuartiles
CUANTILES Deciles
Percentiles

7. Media
Es el valor medio ponderado de la serie de datos. Se
pueden calcular diversos tipos de media, siendo las
más utilizadas:
Media aritmética
Media geométrica
Media armónica

8. Media Aritmética o Promedio
• Es la media aritmética de los valores de una
variable.
• Es la suma de los valores dividido por el tamaño
muestral.
• Conveniente cuando los datos se concentran
simétricamente con respecto a ese valor.
• Muy sensible a valores extremos.
• Es el centro de gravedad de un conjunto de
datos.

9. SIMBOLOGIA
ESTADISTICAS POBLACION MUESTRA
DESCRIPTIVAS
MEDIA
ARITMETICA  x

10. Media Aritmética Para Datos No agrupados
Para un conjunto de datos X1 ………XN, de una población, en su
forma no agrupada, la media aritmética se obtiene sumando todas
las observaciones del conjunto de datos y se divide por el número
total de observaciones de la población , tal como se expresa en la
ecuación:
N
X
  i 1
N
i
( Población)

11. Para un conjunto de datos x1 ………xn, de una muestra, en su
forma no agrupada, la media aritmética se obtiene sumando todas
las observaciones del conjunto de datos y se divide por el número
total de observaciones de la muestra :
n
x i
x i 1
n
( Muestra)

12. Recordando el concepto de datos agrupados…..
Un conjunto de datos no agrupados se
convierten en un conjunto de datos agrupados
cuando éstos son organizados en una distribución
de frecuencias de clase.

13. D
I Media Aritmética Para Datos Agrupados
S
T
R
I
CLASES MC (Xi) fi (Xi)(fi)
B
1 X1 f1 (X1)(f1)
U
C 2 X2 f2 (X2)(f2)
I
O 3 X3 f3 (X3)(f3)
N
4 X4 f4 (X4)(f4)
D
E
. . . .
. . . .
F
R
. . . .
E
C . . . .
U
E . . . .
N
C m Xm fm (Xm)(fm)
I
m m
f X
A
TOTALES i i fi
i 1 i 1

14. m
X i fi
Para la población  i 1
m
i 1
fi
m
X i fi
Para la muestra X  i 1
m
i 1
fi
Nota: El cálculo es el mismo, solo cambia la simbología utilizada

15. La media armónica resulta poco influida por la existencia de
determinados valores mucho más grandes que el conjunto de los
otros, siendo en cambio sensible a valores mucho más pequeños
que el conjunto.
La media armónica no está definida en el caso de la existencia en el
conjunto de valores nulos.

16. La media armónica, representada por H, de una cantidad finita de
números es igual al recíproco, o inverso, de la media aritmética de
los recíprocos de dichos números
Así, dados los números a1,a2, ... , an, (NO AGRUPADOS) la media
armónica será igual a:

17. m
f
i 1
i
M . Armónica 

m  1 
 
 X  * fi
i 1  i 
MGeometric  ( X1 f i ) * ( X 2 f 2 ) * ........( X m f m )
a

18. OTROS TIPOS DE MEDIA
Media geométrica (no agrupados)
Se eleva cada valor al número de veces que se ha repetido
Se multiplican todo estos resultados y al producto final se le
calcula la raíz "n" (siendo "n" el total de datos de la muestra).
1
X  ( X 1  X 2  X 3  ........ X n )
n1 n2 n3 nn n

19. Por ejemplo, la media geométrica de 2 y 18 es
Otro ejemplo, la media de 1, 3 y 9 seria

20. Sólo es relevante la media geométrica si todos los números son
positivos. Si uno de ellos es 0, entonces el resultado es 0. Si hay
un número negativo (o una cantidad impar de ellos) entonces la
media geométrica es, o bien negativa o bien inexistente en los
números reales.
En muchas ocasiones se utiliza su trasformación en el manejo
estadístico de variables con distribución no normal.
La media geométrica es relevante cuando varias cantidades son
sumadas para producir un total.

21. Ventajas:
Se trata de un concepto familiar para la mayoría de las
personas y es intuitivamente claro.
Cada conjunto de datos tiene una media, es una medida que
puede calcularse y es única debido a que cada conjunto
de datos posee una y sólo una media.
MEDIA Es útil para llevar a cabo procedimientos estadísticos como
ARITMETICA la comparación de medias de varios conjuntos de datos.
Desventajas:
Puede verse afectada por valores extremos que no son
representativos del resto de los datos.
Resulta tedioso calcular la media debido a que se utilizan
cada uno de los puntos de datos en su cálculo.
No se puede calcular la media para un conjunto de datos
que tiene clases de extremo abierto, ya sea en el inferior
o en el superior de la escala.

22. Según el tipo de datos que se analice será más apropiado utilizar la
media aritmética o la media geométrica:
• La media geométrica se suele utilizar en series de datos como tipos
de interés anuales, inflación, etc., donde el valor de cada año tiene un
efecto multiplicativo sobre el de los años anteriores.
• En todo caso, la media aritmética es la medida de posición central
más utilizada.
• Lo más positivo de la media es que en su cálculo se utilizan todos
los valores de la serie, por lo que no se pierde ninguna información.
• Sin embargo, presenta el problema de que su valor (tanto en el caso
de la media aritmética como geométrica) se puede ver muy influido
por valores extremos, que se aparten en exceso del resto de la serie.
Estos valores anómalos podrían condicionar en gran medida el valor
de la media, perdiendo ésta representatividad.

23. Se denomina media (aritmética) ponderada de un conjunto de números
al resultado de multiplicar cada uno de los números por un valor
particular para cada uno de ellos, llamado su peso, obteniendo a
continuación la suma de estos productos, y dividiendo el resultado de
esta suma de productos entre la suma de los pesos.
Este "peso" depende de la importancia o significancia de cada uno de
los valores.
O dicho de otro modo es un promedio en el que cada valor de
observación se pondera con algún índice de acuerdo a su importancia.

24. Para una serie de datos
X = { x1, x2, ..., xn}
a la que corresponden los pesos
W = { w1, w2, ..., wn}
la media ponderada se calcula como:
o:
Un ejemplo es la obtención de la media ponderada de las notas de una
materia en la que se asigna distinta importancia (peso) a cada una de las
pruebas de que consta la evaluación.

25. La Media Pesada ó ponderada: permite calcular el
promedio que toma en cuenta la importancia de cada
valor con respecto al total.
X p= Σ (wx)/ Σw
Donde w es el peso asignado a cada observación

26. Mediana
Es el valor del elemento central, cuando los datos están dispuestos en
orden ascendente o descendente.
• Es el valor de la serie de datos ordenados que se sitúa justamente en el centro de la
muestra (un 50% de valores son inferiores y otro 50% son superiores)
• Es conveniente cuando los datos son asimétricos.
• No presentan el problema de estar influido por los valores extremos, pero en cambio
no utiliza en su cálculo toda la información de la serie de datos (no pondera cada valor
por el número de veces que se ha repetido).

27. CALCULO DE LA MEDIANA
Para Datos No agrupados
• Con un número impar de
observaciones:
Para Datos Agrupados
. Se ordenan las observaciones por orden • Se ubica hasta que
de magnitud.
intervalo hay 50% de las
. Se ubica la observación que está en el observaciones.
medio del conjunto de datos.
• Se aplica la fórmula con los
• Con un número par de observaciones: datos de la distribución de
frecuencias.
. Se ordenan las observaciones por
magnitud.
. Se calcula el promedio de las dos
observaciones centrales.

28. Fórmula para el Cálculo de la
Mediana de un Conjunto de Datos
Agrupados
 ( n  1) / 2  f acumuladaa 
Me  LRI   nterior
  cr
 f me 
LRI: límite real inferior de la clase mediana
n: frecuencia total
f acumuladaa
nterior : frecuencia acumulada anterior
al intervalo donde esta localizada la mediana
f me : frecuencia del intervalo donde está localizada
la mediana
Cr: ancho real del intervalo

29. Moda
Es el valor que ocurre con mayor frecuencia en un conjunto
de datos
Es el/los valor/es donde la distribución de frecuencia alcanza
un máximo.
Para Datos No agrupados Para Datos Agrupados
• Es el valor que se repite con • Se ubica el intervalo con la
frecuencia mayor
mayor frecuencia
• Se aplica la fórmula
• Si hay dos valores que se correspondiente para
repiten con mayor frecuencia encontrar la moda
entonces existen dos modas

30. Fórmula para el cálculo de la Moda de un conjunto
de Datos Agrupados
 d1 
Mo  LRI    * cr
 (d1  d 2 
LRI: Límite real inferior de la clase modal
d1: frecuencia de la clase modal menos la frecuencia de la clase
que se encuentra inmediatamente por debajo de ella.
d2: frecuencia de la clase modal menos la frecuencia de la clase
que está por encima de ella
Cr: ancho del intervalo modal

31. De acuerdo al número de modas de un conjunto
de datos se pueden dar los siguientes casos:
UNIMODAL
BIMODAL
MULTIMODAL

32. Ventajas y desventajas de la moda:
•La moda, al igual que la mediana, se puede utilizar como una posición central para datos
tanto cualitativos como cuantitativos.
•También, al igual que la mediana, la moda no se ve mayormente afectada por los valores
extremos. Incluso si los valores extremos son muy altos o muy bajos, se escoge el valor
más frecuente del conjunto de datos como el valor modal.
•Se puede utilizar la moda sin importar qué tan grandes o qué tan pequeños sean los
valores del conjunto de datos, e independientemente de cuál sea su dispersión.
•Se puede utilizar aun cuando una o más clases sean de extremo abierto.
•Muy a menudo, no existe un valor modal debido a que el conjunto de datos no contiene
valores que se presenten más de una vez.
•En otras ocasiones, cada valor es la moda, pues cada uno de ellos se presenta el mismo
número de veces.
Cuando los datos contienen dos, tres o más modas, resultan difíciles de
• interpretar y comparar.

33. ¿Cuál medida de tendencia central se debe utilizar?
• La media aritmética debe utilizarse cuando el conjunto de datos es
homogéneo.
• En una distribución simétrica las tres medidas coinciden, por lo cual se
puede utilizar cualquiera.
• Cuando los datos no son homogéneos se debe utilizar la mediana, ya que
esta no es sensible a los valores extremos, y además no se ve altamente
influida por la frecuencia de aparición de un solo valor.
• Cuando la población está sesgada ya sea positiva o negativamente la
mediana resulta ser la mejor medida de posición.
• La moda se utiliza más que todo para datos categóricos.

34. Medidas de Posición no centrales
Los cuantiles son medidas de posición que se determinan
mediante un método que determina la ubicación de los valores
que dividen un conjunto de observaciones en partes iguales.
Son los valores de la distribución que la dividen en partes iguales,
es decir, en intervalos que comprenden el mismo número de valores.
Cuando la distribución contiene un número alto de intervalos
o de marcas y se requiere obtener un promedio de una parte de ella,
se puede dividir la distribución en cuatro, en diez o en cien partes.

35. Estadísticos de posición
• Se define el cuantil de orden a como un valor de la
variable por debajo del cual se encuentra una
frecuencia acumulada a.
• Casos particulares son los percentiles, cuartiles,
deciles, quintiles,...

36. Cuartiles, Deciles y Percentiles
Cuartiles: son 3 valores que distribuyen la serie de datos,
ordenada de forma creciente o decreciente, en cuatro tramos
iguales, en los que cada uno de ellos concentra el 25% de los
resultados. Dividen el conjunto de datos en 4 partes iguales
Deciles: son 9 valores que distribuyen la serie de datos,
ordenada de forma creciente o decreciente, en diez tramos
iguales, en los que cada uno de ellos concentra el 10% de los
resultados. Dividen el conjunto de datos en 10 partes
iguales
Percentiles: son 99 valores que distribuyen la serie de datos,
ordenada de forma creciente o decreciente, en cien tramos
iguales, en los que cada uno de ellos concentra el 1% de los
resultados. Dividen el conjunto de datos en 100 partes
iguales

37. • Percentil de orden k = cuantil de orden k/100
– La mediana es el percentil 50.
– El percentil de orden 15 deja por debajo al 15% de las
observaciones. Por encima queda el 85%.
• Cuartiles: Dividen a la muestra en 4 grupos con frecuencias
similares.
– Primer cuartil = Percentil 25 = Cuantil 0,25.
– Segundo cuartil = Percentil 50 = Cuantil 0,5 = mediana.
– Tercer cuartil = Percentil 75 = cuantil 0,75.

38. – Ejemplos: El 5% de los recién nacidos tiene un peso demasiado
bajo. ¿Qué peso se considera “demasiado bajo”?
• Percentil 5 o cuantil 0,05.
– ¿Qué peso es superado sólo por el 25% de los individuos?
• Percentil 75.
– El colesterol se distribuye simétricamente en la población. Se
considera patológico los valores extremos. El 90% de los
individuos son normales. ¿Entre qué valores se encuentran los
individuos normales?
• Entre el percentil 5 y el 95.
– ¿Entre qué valores se encuentran la mitad de los individuos “más
normales” de una población?
• Entre el cuartil 1º y 3º.

39. Los cuartiles son los tres valores que dividen al conjunto de datos
ordenados en cuatro partes porcentualmente iguales.
Hay tres cuartiles denotados usualmente Q1, Q2, Q3. El segundo cuartil
es precisamente la mediana. El primer cuartil, es el valor en el cual o por
debajo del cual queda un cuarto (25%) de todos los valores de la
sucesión (ordenada); el tercer cuartil, es el valor en el cual o por debajo
del cual quedan las tres cuartas partes (75%) de los datos.
Los deciles son ciertos números que dividen la sucesión de datos
ordenados en diez partes porcentualmente iguales. Son los nueve
valores que dividen al conjunto de datos ordenados en diez partes
iguales, son también un caso particular de los percentiles. Los deciles
se denotan D1, D2,..., D9, que se leen primer decil, segundo decil,
etc.
Los deciles, al igual que los cuartiles, son ampliamente utilizados para
fijar el aprovechamiento académico.

40. Los percentiles son, tal vez, las medidas más utilizadas para
propósitos de ubicación o clasificación de las personas
cuando atienden características tales como peso, estatura, etc.
Los percentiles son ciertos números que dividen la sucesión
de datos ordenados en cien partes porcentualmente iguales.
Estos son los 99 valores que dividen en cien partes iguales el
conjunto de datos ordenados. Los percentiles (P1, P2,... P99),
leídos primer percentil,..., percentil 99.

41. Cálculo de los Cuantiles
Para Datos No agrupados
• Se ordenan las observaciones Para Datos Agrupados
por magnitud • Se ubica hasta que
intervalo están el 25% ó el
• Se divide el conjunto de datos
10% de las observaciones
en 4 partes iguales, o 10 partes
iguales o 100 partes iguales • Se aplica la fórmula
• Luego se localizan los
valores de los cuantiles

42. Fórmula General para los Cuantiles
Datos Agrupados
Me = LRI + [( k(n+1)/p – faca)/ fmp] * Cr
LRI: límite real inferior del cuantil
n: frecuencia total
faca: frecuencia acumulada anterior al intervalo donde está localizado
el cuantil
fmp: frecuencia del intervalo donde está localizado el cuantil
Cr: ancho real del intervalo
Si se desean calcular los cuartiles p =4
Si se desea calcular los deciles p= 10
Si se desea calcular los percentiles p= 100

43. Medidas Descriptivas
Tendencia Central Variabilidad Forma
Y Posición
• Media • Rango • Sesgo
• Curtosis
• Mediana • Desviación Típica
• Simetría
• Moda •Varianza
• Cuartiles • Coeficiente de
• Deciles Variación
• Percentiles

44. Medidas de Variabilidad
Se refiere a la extensión de los datos de una distribución, es
decir el grado en que las observaciones se distribuyen
• Rango
• Desviación Típica
• Varianza
• Coeficiente de Variación

45. Importancia de la dispersión
 Proporciona información adicional que permite juzgar la
confiabilidad de la medida de tendencia central. Si los datos se
encuentran ampliamente dispersos, la posición central es menos
representativa de los datos.
 Ya que existen problemas característicos para datos
ampliamente dispersos, debemos ser capaces de distinguir que
presentan esa dispersión antes de abordar esos problemas.
 Quizá se desee comparar las dispersiones de diferentes
muestras. Si no se desea tener una amplia dispersión de valores
con respecto al centro de distribución o ésto presenta riesgos
inaceptables, necesitamos tener habilidad de reconocerlo y
evitar escoger distribuciones que tengan las dispersiones más
grandes.

46. Ejemplo pg 71lind marchal wathen

47. Medidas De Variabilidad
Rango : mide la amplitud de los valores de la población o de
una muestra
Es la diferencia entre el valor mayor y el valor menor de un
conjunto de datos
R  Vmayor  Vmenor Datos no
agrupados
R  LRSloultimointervalo  LRI primerint ervalo Datos agrupados

48. Varianza :
Mide la distancia existente entre los valores de la serie y la
media.
Se calcula como la sumatoria de las diferencias al cuadrado
entre cada valor y la media, multiplicadas por el número de
veces que se ha repetido cada valor.
Es la dispersión de los datos alrededor de la media.
Es un indicador de la variabilidad expresado en unidades
cuadradas.

49. Desviación Típica ó estándar
Es la raíz cuadrada de la sumatoria de los cuadrados de las
desviaciones respecto a la media.
Es un indicador de la variabilidad expresado en unidades
absolutas.

50. Calculo de Varianza para Datos No Agrupados
N
2
 (Xi  )
 
2 i 1
Población N
N
(X i  X) 2

2 i 1
Muestra S n 1

51. Cálculo de Desviación Estándar Datos No Agrupados
N
(X i  ) 2
Población  i 1
N
N
(X i  X) 2
Muestra S i 1
n 1

52. Ecuaciones para el cálculo de la
varianza y la desviación estándar para
datos agrupados

53. SIMBOLOGIA
ESTADISTICAS POBLACION MUESTRA
DESCRIPTIVAS
VARIANZA

2 2
S
DESVIACION
STANDARD
 S

54. Para un conjunto de datos de una población que se agrupa en una distribución de frecuencias
CLASES MC (Xi) fi ( X i   ) ( X i   ) fi
2 2
1 X1 f1 ( X 1   ) ( X 1   ) f1
2 2
2 X2 f2 ( X 2  ) 2
( X 2   )2 f 2
3 X3 f3 ( X 3   )2 ( X 3   )2 f3
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
m Xm fm . .
m m
Totales f
i 1
i (X
i 1
i  ) f i
2

55. DE LOS DATOS DE LA TABLA ANTERIOR SE
OBTIENE EL CALCULO DE LA VARIANZA DE LA
POBLACION POR LA EXPRESION:
m
2
 ( Xi  ) fi
 2
 i 1
m
 f
i 1 i

56. CALCULO DE LA DESVIACION ESTANDAR
DE LA POBLACION
m 2
 (Xi  ) fi
 i 1
m
 f
i 1 i

57. Para una muestra
CLASES MC (Xi) fi ( X i  X ) ( X i  X ) fi
2 2
1 X1 f1 ( X1  X ) ( X1  X ) f1
2 2
2 X2 f2 ( X 2  X ) ( X 2  X ) f2
2 2
3 X3 f3 ( X 3  X )2 ( X 3  X )2 f3
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
m Xm fm . .
m m
Totales f
i 1
i (X
i 1
i X ) f i
2

58. CALCULO DE LA VARIANZA DE LA MUESTRA
m
2
 ( xi  x ) fi
2 i 1
 m
S  f 1  n 1
i 1 i
¿Por qué utilizamos n – 1 como denominador en lugar de n? Los especialistas en
estadística pueden demostrar que si tomamos muchas muestras de una población dada, si
encontramos la varianza de la muestra para cada muestra y promediamos los resultados,
entonces este promedio no tiende a tomar el valor de la varianza de la población, a menos
que tomemos n – 1 como denominador de los cálculos.

59. CALCULO DE LA DESVIACION ESTANDAR
DE LA MUESTRA
m 2
 ( xi  x ) fi
S i 1
m
 f 1
i 1 i

60. Usos de la desviación estándar
Teorema de Chebyshev
La desviación estándar nos permite determinar, con un buen
grado de precisión, dónde están localizados los valores de una
distribución de frecuencias con relación a la media. El
teorema de Chebyshev dice que no importa qué forma tenga la
distribución, al menos 75% de los valores caen dentro de + 2
desviaciones estándar a partir de la media de la distribución, y
al menos 89% de los valores caen dentro de + 3 desviaciones
estándar a partir de la media.

61. Pgs 81 y 82 lind marchalwatten

62. Para distribuciones simétricas:
Teorema de la Normal
Aproximadamente 68% de los valores de la población cae
dentro de + 1 desviación estándar a partir de la media.
Aproximadamente 95% de los valores estará dentro de + 2
desviaciones estándar a partir de la media.
Aproximadamente 99% de los valores estará en el intervalo
que va desde tres desviaciones estándar por debajo de la
media hasta tres desviaciones estándar por arriba de la media.

63. Coeficiente de Variación
Es una medida relativa de dispersión, en la cual se expresa la
desviación estándar como un porcentaje de la media.
Resulta útil al comparar la cantidad de variación en grupos de
datos que posean medias diferentes.
Se calcula como cociente entre la desviación típica y la media.
El interés del coeficiente de variación es que al ser un
porcentaje permite comparar el nivel de dispersión de dos
muestras. Esto no ocurre con la desviación típica, ya que viene
expresada en las mismas unidades que los datos de la serie.
Por ejemplo, para comparar el nivel de dispersión de una serie
de datos de la altura de los alumnos de una clase y otra serie
con el peso de dichos alumnos, no se puede utilizar las
desviaciones típicas (una viene expresada en cm y la otra en
kg). En cambio, sus coeficientes de variación son ambos
porcentajes, por lo que sí se pueden comparar.

64. Coeficiente de variación
La desviación estándar es una medida absoluta de la dispersión que expresa la
variación en las mismas unidades que los datos originales.
La desviación estándar no puede ser la única base para la comparación de dos
distribuciones. Si tenemos una desviación estándar de 10 y una media de 5, los
valores varían en una cantidad que es el doble de la media misma. Si, por otro lado,
tenemos una desviación estándar de 10 y una media de 5.000, la variación con
respecto a la media es insignificante. En consecuencia, no podemos conocer la
dispersión de un conjunto de datos hasta que conocemos su desviación estándar, su
media y cómo se compara la desviación estándar con respecto a la media.
Lo que necesitamos es una medida relativa que nos proporcione una estimación de la
magnitud de la desviación con respecto a la magnitud de la media. El coeficiente de
variación es una de estas medidas relativas de dispersión. Se relaciona la desviación
estándar y la media, expresando la desviación estándar como porcentaje de la media.

65. Coeficiente de variación
• Es la razón entre la desviación típica y la media.
S
– Mide la desviación típica en forma de
“qué tamaño tiene con respecto a la media” CV 
– También se la denomina variabilidad relativa.
– Es frecuente mostrarla en porcentajes
x
• Si la media es 80 y la desviación típica 20 entonces CV=20/80=0,25=25%
(variabilidad relativa)
• Es una cantidad adimensional. Interesante para comparar la variabilidad
de diferentes variables.
– Si el peso tiene CV=30% y la altura tiene CV=10%, los individuos
presentan más dispersión en peso que en altura.
• No debe usarse cuando la variable presenta valores negativos o donde el
valor 0 sea una cantidad fijada arbitrariamente.
– Por ejemplo 0ºC ≠ 0ºF

66. 
PARA LA POBLACION
CV 

S
PARA LA MUESTRA cv 
X

67. ESTADISTICAS POBLACION MUESTRA
DESCRIPTIVAS
MEDIA
 x
VARIANZA

2 2
S
DESVIACION
STANDARD
 S
COEFICIENTE
DE VARIACION
CV cv

68. Otras Medidas de Dispersión
• Miden el grado de dispersión (variabilidad)
de los datos, independientemente de su causa.
• Amplitud o Rango („range‟):
La diferencia entre las
observaciones extremas.
– 2,1,4,3,8,4. El rango es 8-1=7
– Es muy sensible a los valores
extremos.
• Rango intercuartílico („interquartile range‟):
– Es la distancia entre el primer y tercer cuartil.
• Rango intercuartílico = P75 - P25
– Parecida al rango, pero eliminando las observaciones más extremas
inferiores y superiores.
– No es tan sensible a valores extremos.

69. Fr
1
0.75
0.5
0.25
Recorrido o rango
intercuartílico
0
P25 P50 P75 x
Q1 Q2 Q3
mediana

70. Medidas de forma: Grado de concentración
Las medidas de forma permiten conocer que forma tiene la curva que representa la
serie de datos de la muestra. Forma es el patrón de distribución de los valores de los
datos a través del rango de todos los valores.
La distribución puede ser simétrica cuando los valores pequeños y grandes se equilibran
entre si. Puede ser asimétrica cuando muestra un desequilibrio entre los valores
pequeños y grandes.
En concreto, podemos estudiar las siguientes características de la curva:
Concentración: mide si los valores de la variable están más o menos uniformemente
repartidos a lo largo de la muestra.
Asimetría: mide si la curva tiene una forma simétrica, es decir, si respecto al centro de
la misma (centro de simetría) los segmentos de curva que quedan a derecha e izquierda
son similares.
Curtosis: mide si los valores de la distribución están más o menos concentrados
alrededor de los valores medios de la muestra.

71. Para medir el nivel de concentración de una distribución de
frecuencia se pueden utilizar distintos indicadores, entre
ellos el Indice de Gini.
Este índice se calcula aplicando la siguiente fórmula:
En donde los valores de la fórmula se basan en las
proporciones acumuladas de las dos variables que se analizan.

72. El Indice Gini (IG) puede tomar valores entre 0 y 1:
IG = 0 : concentración mínima. La muestra está
uniformemente repartida a lo largo de todo su rango.
IG = 1 : concentración máxima. Un sólo valor de la
muestra acumula el 100% de los resultados.

73. Asimetría
El concepto de asimetría se refiere a si la curva que forman los
valores de la serie presenta la misma forma a izquierda y derecha
de un valor central (media aritmética)
Para medir el nivel de asimetría se utiliza el llamado Coeficiente
de Asimetría de Fisher, que viene definido:

74. Los resultados pueden ser los siguientes:
g1 = 0 (distribución simétrica; existe la misma
concentración de valores a la derecha y a la
izquierda de la media)
g1 > 0 (distribución asimétrica positiva; existe
mayor concentración de valores a la izquierda de la
media que a su derecha)
g1 < 0 (distribución asimétrica negativa; existe
mayor concentración de valores a la derecha de la
media que a su izquierda)

75. Asimetría o sesgo
• Una distribución es simétrica si la mitad izquierda de su distribución es la imagen
especular de su mitad derecha.
• En las distribuciones simétricas la media y la mediana coinciden. Si sólo hay una
moda también coincide.
• La asimetría es positiva o negativa en función de a qué lado se encuentra la cola de la
distribución.
• La media tiende a desplazarse hacia las valores extremos (colas).
Media < mediana asimétrica negativa o sesgo negativo
La mayoría de los valores están en la parte inferior de la distribución. La distorsión
hacia la izquierda es provocada por algunos valores muy pequeños.
Media = mediana simétrica o asimetría cero
.
Media > mediana asimétrica o positiva o sesgo derecho
La mayoría de los valores están en la parte superior de la distribución. La distorsión
hacia la derecha es provocada por algunos valores muy grandes.
• Las discrepancias entre las medidas de centralización son indicación de asimetría.

76. Las curvas que representan los puntos de datos de un conjunto de datos pueden
ser simétricas o sesgadas.
Las curvas simétricas, tienen una forma tal que una línea vertical que pase por
el punto más alto de la curva dividirá el área de ésta en dos partes iguales. Cada
parte es una imagen espejo de la otra.
En las curvas sesgadas, los valores de su distribución de frecuencias están
concentrados en el extremo inferior o en el superior de la escala de medición
del eje horizontal. Los valores no están igualmente distribuidos.
Las curvas pueden estar sesgadas hacia la derecha (positivamente sesgadas) o
sesgadas hacia la izquierda (negativamente sesgadas).

79. El Coeficiente de Curtosis analiza el grado de concentración
que presentan los valores alrededor de la zona central de la
distribución. La curtosis nos indica el grado de apuntamiento
(aplastamiento) de una distribución con respecto a la
distribución normal o gaussiana. Es adimensional.
Se definen 3 tipos de distribuciones según su grado de
curtosis:
Distribución mesocúrtica: presenta un grado de
concentración medio alrededor de los valores centrales de la
variable (el mismo que presenta una distribución normal).
Distribución leptocúrtica: presenta un elevado grado de
concentración alrededor de los valores centrales de la variable.
Distribución platicúrtica: presenta un reducido grado de
concentración alrededor de los valores centrales de la variable.

80. El Coeficiente de Curtosis viene definido por la siguiente
fórmula:

81. Los resultados pueden ser los siguientes:
g2 = 0 (distribución mesocúrtica)
.
g2 > 0 (distribución leptocúrtica)
.
g2 < 0 (distribución platicúrtica
Cuando medimos la curtosis de una distribución,
estamos midiendo su grado de agudeza.

82. Los gráficos poseen la misma media y desviación
típica, pero diferente grado de apuntamiento o
curtosis.
300
400
160
140
300
200
120
100 200
100
80
Frecuencia
100
Frecuencia
60
0
40 0
27 37 45 53 61 69 77 85 93
45 48 51 54 57 60 63 66 69 72 75 78 81 84 3 27 37 47 57 67 77 87 97 108
32 41 49 57 65 73 81 89 99
16 32 42 52 62 72 82 92 102 138
Platicúrtica
Mesocúrtica
Leptocúrtica

83. ¿Cómo seleccionar una medida de tendencia que represente los datos?
Cuando trabajamos un problema de estadística, debemos decidir si vamos a utilizar la
media, la mediana o la moda como medidas de tendencia central. Las distribuciones
simétricas que sólo contienen una moda, siempre tienen el mismo valor para la media, la
mediana y la moda. En tales casos, no es necesario escoger la medida de tendencia central,
pues ya está hecha la selección.
En una distribución positivamente sesgada (es decir, sesgada hacia la derecha), la moda
todavía se encuentra en el punto más alto de la distribución, la mediana está hacia la
derecha de la moda y la media se encuentra todavía más a la derecha de la moda y la
mediana.
En una distribución negativamente sesgada, la moda sigue siendo el punto más alto de la
distribución, la mediana está hacia la izquierda de ella y la media se encuentra todavía más
a la izquierda de la moda y la mediana.
Cuando la población está sesgada negativa o positivamente, con frecuencia la mediana
resulta ser la mejor medida de posición, debido a que siempre está entre la moda y la media.
La mediana no se ve altamente influida por la frecuencia de aparición de un solo valor
como es el caso de la moda, ni se distorsiona con la presencia de valores extremos como la
media.
Resumiendo