Este documento presenta conceptos clave sobre variables aleatorias continuas. Explica que una variable aleatoria continua puede representarse mediante una función de densidad de probabilidad f(x) o una función de distribución acumulativa F(x). También proporciona ejemplos numéricos de cómo calcular probabilidades utilizando estas funciones. Finalmente, describe algunas medidas características comunes de una variable aleatoria continua como la esperanza matemática y la varianza.

1. 3. Distribuciones de variables aleatorias (8/13)
Variable aleatoria continua
a) Representación diferencial: función de densidad, f(x)
CÁLCULO DE PROBABILIDADES CON LA FUNCIÓN DE DENSIDAD
Probabilidades y Estadística I

2. 3. Distribuciones de variables aleatorias (9/13)
Variable aleatoria continua
a) Representación diferencial: origen de f(x)
Histograma para 20 clases Histograma para 50 clases
400 200
160
300
120
200
80
100 40
0 0
-5 -3 -1 1 3 5 7 -5 -3 -1 1 3 5 7
Probabilidades y Estadística I

3. 3. Distribuciones de variables aleatorias (10/13)
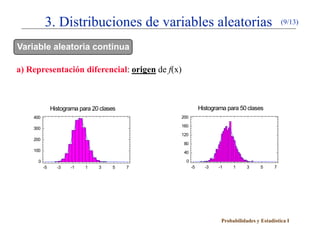
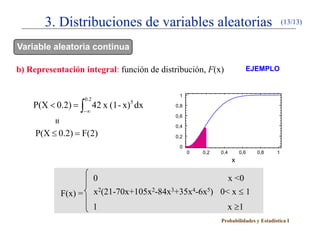
Variable aleatoria continua
a) Representación diferencial: función de densidad, f(x) EJEMPLO
X ≡ “proporción de accidentes automovilísticos mortales” Rg X ≡ [0,1]
3
2,5
42 x (1-x) 5 0< x ≤ 1 2
f(x) = 1,5
0 en otro caso 1
0,5
0
0 0,2 0,4 0,6 0,8 1
x
0.3
P(0.2 < X < 0.3) = ∫ 42 x (1 - x) 5 dx
0.2
Probabilidades y Estadística I

4. 3. Distribuciones de variables aleatorias (11/13)
Variable aleatoria continua
b) Representación integral: función de distribución, F(x) (continua)
PROPIEDADES
Probabilidades y Estadística I

5. 3. Distribuciones de variables aleatorias (12/13)
Variable aleatoria continua
b) Representación integral: función de distribución, F(x) PROPIEDADES
CÁLCULO DE PROBABILIDADES CON LA FUNCIÓN DE DISTRIBUCIÓN
RELACIÓN ESPECIAL ENTRE F(x) Y f(x)
Probabilidades y Estadística I

6. 3. Distribuciones de variables aleatorias (13/13)
Variable aleatoria continua
b) Representación integral: función de distribución, F(x) EJEMPLO
1
0.2
P(X < 0.2) = ∫ 42 x (1 - x) 5 dx 0,8
−∞
0,6
=
0,4
P(X ≤ 0.2) = F(2) 0,2
0
0 0,2 0,4 0,6 0,8 1
x
0 x <0
F(x) = x2(21-70x+105x2-84x3+35x4-6x5) 0< x ≤ 1
1 x ≥1
Probabilidades y Estadística I

7. Esquema inicial
1. Variable aleatoria. Concepto
2. Tipos de variables aleatorias
3. Distribuciones de probabilidad de variables aleatorias
4. Medidas características de una variable aleatoria
5. Desigualdad de Tchebychev
Probabilidades y Estadística I

8. 4. Medidas características de una v.a. (1/4)
Esperanza matemática (definición)
(caso discreto) E[X ]
= ∑ xp( x)
= µ
x
(caso discreto) E[X ]
= ∫=
xf ( x)dx µ
RELACIÓN CON LA ESTRUCTURA DE LA MEDIA ARITMÉTICA
k
X = ∑ fi x 'i
i =1
PROPIEDAD E [ aX + b ] aE [ X ] + b
=
Probabilidades y Estadística I

9. 4. Medidas características de una v.a. (2/4)
Varianza (definición)
(caso discreto) Var [ X ] = ( x − µ ) 2 p ( x) =
∑ σ2
x
(caso discreto) Var [ X ] = ) 2 f ( x)dx =
∫ (x − µ σ2
PROPIEDAD Var [ aX + b ] =Var [ X ]
a2
Probabilidades y Estadística I

10. 4. Medidas características de una v.a. (3/4)
Mediana F(x) = ½
Moda Max f (x)
Percentiles F(x) = i/100
Cuartiles F(x) = i/4
GENERALIZACIONES DESDE ESTADÍSTICA DESCRIPTIVA
Probabilidades y Estadística I

11. 4. Medidas características de una v.a. (4/4)
Momento centrado en el origen
Caso especial
αr = E  X r 
  = E[X ] µ
α1 =
Momento centrado en la media
Caso especial
= E ( X − µ ) 
µr
r
  µ2 = E ( X − µ ) 2  = Var [ X ] = σ 2
 
µ2 α 2 − α12
=
Probabilidades y Estadística I

12. Esquema inicial
1. Variable aleatoria. Concepto
2. Tipos de variables aleatorias
3. Distribuciones de probabilidad de variables aleatorias
4. Medidas características de una variable aleatoria
5. Desigualdad de Tchebychev
Probabilidades y Estadística I

13. 5. Relaciones entre media y varianza
Desigualdad de Tchebychev
P ( X − µ > kσ ) ≤ 2 ⇔ P ( X − µ ≤ kσ ) > 1 − 2
1 1
k k
1
P ( µ − kσ ≤ X ≤ µ + kσ ) > 1 − 2
k
Normalización de una v.a
X −µ
σ
Probabilidades y Estadística I