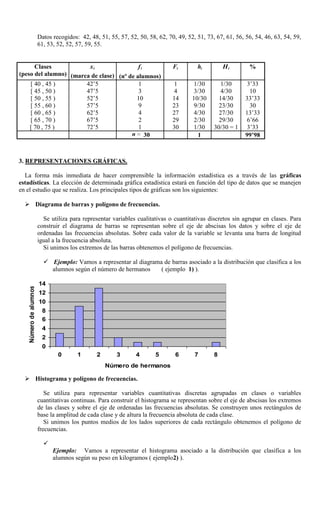
Este documento introduce conceptos básicos de estadística como población, muestra, variables cualitativas y cuantitativas, frecuencias absolutas y relativas, y tablas y representaciones estadísticas. Explica que la estadística estudia fenómenos a partir de datos de muestras representativas, y define términos como población, muestra, variable cualitativa y cuantitativa. También describe cómo construir tablas estadísticas con frecuencias absolutas y relativas, y diferentes tipos de grá

1. ESTADÍSTICA
La ESTADÍSTICA es la parte de las Matemáticas que tiene por objeto estudiar fenómenos físicos,
biológicos, económicos, sociales, etc. , a partir de datos recogidos de numerosas experiencias u
observaciones.
1. INFORMACIÓN ESTADÍSTICA. CONCEPTOS BÁSICOS.
El conjunto de todos los elementos que cumplen una determinada característica y sobre el que se desea
obtener información se denomina población. La población viene representada usualmente por la letra N.
Cada uno de los elementos que forman la población es un individuo.
Para recoger información acerca de la población se realiza una encuesta. Esta recogida de información se
hace bien por observación o mediante preguntas.
Por razones de economía, tiempo o necesidad, en Estadística no se trabaja con el total de la población, sino
con una parte de la misma.
Una muestra es cualquier subconjunto o parte de la población. Esta muestra tiene que ser representativa de
toda la población objeto de estudio. Uno de los procesos para elegir de manera adecuada una muestra es
el muestreo aleatorio; en él, todos los elementos de la población tienen la misma probabilidad de ser incluidos
en la muestra. El tamaño de la muestra se representa mediante la letra n.
 Ejemplos :
a) Población: Socios de un club de tenis ( 500 personas (300 hombres y 200
mujeres) ). N = 500.
Muestra: 10 % de los socios ( 50 personas (30 hombres y 20 mujeres) ). n = 50.
b) Población: Ciudadanos con derecho a voto ( 4 millones (2’5 millones hombres
y 1’5 millones mujeres) ). N = 4.000.000.
Muestra: 1 ‰ de la población ( 4.000 personas (2.500 hombres y 1.500
mujeres) ). n = 4.000.
2. VARIABLES ESTADÍSTICAS.
Cada uno de los aspectos que se desea conocer acerca de la población se denomina variable estadística. Las
variables estadísticas pueden ser:
 Cualitativas: si se pueden observar o leer, pero no se pueden contar o medir. Por ejemplo: color de pelo,
lugar de nacimiento, profesión.
 Cuantitativas: si se pueden contar o medir. Por ejemplo: número de hermanos, peso, número de discos
vendidos, talla.
Las variables estadísticas cuantitativas pueden ser discretas o continuas:
Una variable estadística cuantitativa es discreta cuando sólo toma un número finito de valores
aislados (es decir, se puede contar). Por ejemplo: número de hermanos, número de discos vendidos,
número de pulsaciones.
Una variable estadística cuantitativa es continua cuando puede tomar todos los valores posibles de
un intervalo (es decir, se puede medir). Por ejemplo: peso, talla, medida del salto de longitud.
Los valores de una variable estadística se representan por
x1 , x2 , x3 ,, x k
Observación:
En algunos textos se habla de caracteres estadísticos cualitativos y cuantitativos, y sólo se consideran
variables estadísticas las cuantitativas, es decir las que se pueden medir.
3. FRECUENCIAS ABSOLUTAS Y RELATIVAS. TABLAS ESTADÍSTICAS.
Con los datos desordenados obtenidos en la encuesta, se construyen unas tablas ordenadas. Estas tablas
recogen el número de individuos que toma los diferentes valores de la variable, son las frecuencias.

2. Frecuencia absoluta de un valor de la variable es el número de veces que se repite dicho valor.
La frecuencia absoluta del valor x i se representa por f i .
La correspondencia que asocia a cada valor de la variable su frecuencia absoluta se llama distribución
estadística.
Frecuencia relativa de un valor de la variable es el cociente entre la frecuencia absoluta del valor y el
número total de datos.
La frecuencia relativa del valor x i se representa por hi , por tanto
fi
hi
n
Frecuencia absoluta acumulada de un valor de la variable, x i , es la suma de las frecuencias absolutas
de los valores menores o iguales a x i .
La frecuencia absoluta acumulada del valor x i se representa por Fi , así tenemos que
Fi f1 f2  f i
Frecuencia relativa acumulada de un valor de la variable, x i , es el cociente entre la frecuencia
absoluta acumulada del valor x i y el número total de datos.
La frecuencia relativa acumulada del valor x i se representa por H i , así tenemos que
Fi f1 f2  f i f1 f2 f
Hi  i h1 h2  hi
n n n n n
Para construir las tablas estadísticas formaremos varias columnas: una en la que figuren los valores de la
variable, otra de frecuencias absolutas, otra de frecuencias relativas, otra de frecuencias absolutas acumuladas,
otra de frecuencias relativas acumuladas y otra de porcentajes.
Si la variable estadística es discreta con un número grande de datos (por ejemplo, número de discos vendidos)
o es continua, se realiza un agrupamiento de los datos en intervalos, que en Estadística se denominan clases.
Para realizar un buen agrupamiento debemos tener en cuenta los siguientes puntos:
- Es aconsejable escoger los extremos inferior y superior de cada intervalo de modo que se sitúen en
números “redondos”; por ejemplo, múltiplos de 5, de 10, etc.
- Todas las clases deben tener la misma amplitud.
- Los puntos medios de cada clase se llaman marcas de clase.
- El número de clases que debemos formar es de libre elección, pero existe un criterio general que aconseja
formar tantas clases como la raíz cuadrada del número total de datos.
 Ejemplos :
1) En un centro de enseñanza secundaria hay ocho clases de tercero de E.S.O. y se quiere tener una
información sobre el número de hermanos de los alumnos.
Variable: Número de hermanos del alumno (var. estad. cuantitativa discreta).
Población: Curso de 3º de E.S.O.
Muestra: 30 alumnos seleccionados al azar de las ocho clases. n = 30.
x i (nº de hermanos) f i (nº de alumnos) Fi hi Hi %
0 3 3 3/30 3/30 10
1 9 12 9/30 12/30 30
2 13 25 13/30 25/30 43’33
3 2 27 2/30 27/30 6’66
4 1 28 1/30 28/30 3’33
5 1 29 1/30 29/30 3’33
8 1 30 1/30 30/30 = 1 3’33
n 30 1 99’98
2) En un centro de enseñanza secundaria hay ocho clases de tercero de E.S.O. y se quiere tener una
información sobre el peso de los alumnos.
Variable: Peso de los alumnos (var. estad. cuantitativa continua).
Población: Curso de 3º de E.S.O.
Muestra: 30 alumnos seleccionados al azar de las ocho clases. n = 30.

3. Datos recogidos: 42, 48, 51, 55, 57, 52, 50, 58, 62, 70, 49, 52, 51, 73, 67, 61, 56, 56, 54, 46, 63, 54, 59,
61, 53, 52, 52, 57, 59, 55.
Clases xi fi Fi hi Hi %
(peso del alumno) (marca de clase) (nº de alumnos)
[ 40 , 45 ) 42’5 1 1 1/30 1/30 3’33
[ 45 , 50 ) 47’5 3 4 3/30 4/30 10
[ 50 , 55 ) 52’5 10 14 10/30 14/30 33’33
[ 55 , 60 ) 57’5 9 23 9/30 23/30 30
[ 60 , 65 ) 62’5 4 27 4/30 27/30 13’33
[ 65 , 70 ) 67’5 2 29 2/30 29/30 6’66
[ 70 , 75 ) 72’5 1 30 1/30 30/30 = 1 3’33
n 30 1 99’98
3. REPRESENTACIONES GRÁFICAS.
La forma más inmediata de hacer comprensible la información estadística es a través de las gráficas
estadísticas. La elección de determinada gráfica estadística estará en función del tipo de datos que se manejen
en el estudio que se realiza. Los principales tipos de gráficas son los siguientes:
 Diagrama de barras y polígono de frecuencias.
Se utiliza para representar variables cualitativas o cuantitativas discretos sin agrupar en clases. Para
construir el diagrama de barras se representan sobre el eje de abscisas los datos y sobre el eje de
ordenadas las frecuencias absolutas. Sobre cada valor de la variable se levanta una barra de longitud
igual a la frecuencia absoluta.
Si unimos los extremos de las barras obtenemos el polígono de frecuencias.
 Ejemplo: Vamos a representar al diagrama de barras asociado a la distribución que clasifica a los
alumnos según el número de hermanos ( ejemplo 1) ).
14
Número de alumnos
12
10
8
6
4
2
0
0 1 2 3 4 5 6 7 8
Número de hermanos
 Histograma y polígono de frecuencias.
Se utiliza para representar variables cuantitativas discretas agrupadas en clases o variables
cuantitativas continuas. Para construir el histograma se representan sobre el eje de abscisas los extremos
de las clases y sobre el eje de ordenadas las frecuencias absolutas. Se construyen unos rectángulos de
base la amplitud de cada clase y de altura la frecuencia absoluta de cada clase.
Si unimos los puntos medios de los lados superiores de cada rectángulo obtenemos el polígono de
frecuencias.

Ejemplo: Vamos a representar el histograma asociado a la distribución que clasifica a los
alumnos según su peso en kilogramos ( ejemplo2) ).

4. 12
10
8
Número de
6
alumnos
4
2
0
40 45 50 55 60 65 70 75
Peso en Kg.
 Diagrama de sectores.
Se utiliza para representar fundamentalmente variables cualitativas. Consiste en un círculo dividido en
tantos sectores circulares como modalidades tiene la variable. El ángulo central de cada sector ha de ser
proporcional a la frecuencia absoluta correspondiente.
Para calcular la medida del ángulo se hace la siguiente operación: hi 360º
 Ejemplo: Se realiza sobre la población y muestra de los ejemplos 1) y 2) el estudio de la variable
cualitativa “Autonomía de nacimiento del alumno”.
Vamos a representar mediante un diagrama de sectores la distribución estadística que clasifica a los
alumnos según la autonomía de nacimiento.
Para el cálculo del ángulo central procedemos así:
Autonomía Número de Medida
alumnos del ángulo central
Andalucía 19 19
360º 228º
30
Castilla-La Mancha 7 7
360º 84º
30
Cataluña 2 2
360º 24º
30
Galicia 1 1
360º 12º
30
País Vasco 1 1
360º 12º
30
El diagrama de sectores asociado sería el siguiente:
Andalucía
Castilla-La Mancha
Cataluña
Galicia
País Vasco

5. 4. PARÁMETROS ESTADÍSTICOS.
Observación:
El cálculo de parámetros estadísticos se restringe a las variables estadísticas cuantitativas. No podemos
calcular parámetros de variables cualitativas, aunque si podemos hacer sus tablas de frecuencias y representarlas
gráficamente.
 MEDIDAS DE CENTRALIZACIÓN.
Se llaman medidas de centralización a los parámetros que tienden a situarse hacia el centro del conjunto de
datos ordenados. Las medidas de centralización son valores que representan el conjunto de los datos.
Las medidas de centralización más importantes son: la media aritmética, la mediana y la moda.
 Media aritmética.
La media aritmética de una variable estadística es el cociente entre la suma de todos los valores de la
variable y el número de éstos (tamaño muestral). Se representa por x .
Si la variable toma los valores x i con frecuencias absolutas f i , la media aritmética es:
k
xi fi
x1 f 1 x2 f2  x k f k i 1
x
n n
Si los datos están agrupados en clases, se toma para x i las marcas de clase.
 Ejemplos :
0 3 1 9 2 13 3 2 4 1 5 1 8 1 
x 193
'
1) 30
42'5 1 47'5 3 52'5 10 57'5 9 62'5 4 67'5 2 72'5 1 
x 5616
'
2) 30
 Mediana.
La mediana de una variable estadística es el valor de la variable que ocupa el lugar central de los datos.
Se representa por Me.
Si el número de datos es impar se toma como valor de la mediana el valor central.
Si el número de datos es par se toma como valor de la mediana la media aritmética de los dos valores
centrales.
 Ejemplos :
1) Me = 2 ( los valores 15º y 16º son 2 )
2) Me = 57’5 ( los valores 15º y 16º están en la clase [55,60) )
 Moda.
La moda de una variable estadística es el valor de la variable que tiene mayor frecuencia absoluta. Se
representa por Mo.
Si los datos están agrupados en clases se toma como valor de la moda la marca de la clase que tiene
mayor frecuencia absoluta. Esta clase se llama clase modal.
 Ejemplos :
1) Mo = 2 . 2) Mo = [50,55) .
 MEDIDAS DE DISPERSIÓN.
Se llaman medidas de dispersión a los parámetros que miden las desviaciones respecto de la media. Las
medidas de dispersión amplían la información sobre la distribución de los datos, estableciendo si están más o
menos próximos unos de otros.
Las medidas de dispersión más importantes son :el rango o recorrido, la varianza y la desviación típica.
 Rango o recorrido.

6. El rango o recorrido de una variable estadística es la diferencia entre el mayor y el menor valor de la
variable.
Esta medida tiene el inconveniente de que sólo depende de los valores extremos de la variable.
 Ejemplos :
1) Rango = 8 – 0 = 8 . 2) Rango = 72’5 – 42’5 = 30 .
 Varianza.
La varianza de una variable estadística es la media aritmética de los cuadrados de las desviaciones
2
respecto a la media. Se representa por .
k
2
2 2 2 fi xi x
2 f1 x1 x f2 x2 x  fk xk x i 1
n n
 Ejemplos :
2
 2

1) 2'395 . 2) 415 .
'
 Desviación típica.
La desviación típica de una variable estadística es la raíz cuadrada positiva de la varianza. Se
representa por .
 Ejemplos :
1) 1547 .
' 2) 6'446 .