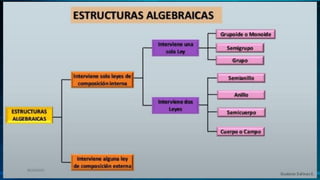
El documento describe las estructuras algebraicas más importantes, incluyendo aquellas con una operación interna como grupos y anillos, aquellas con dos operaciones internas como semianillos y cuerpos, y aquellas con una operación interna y otra externa como espacios vectoriales. Define cada estructura y sus propiedades matemáticas fundamentales.

1. ESTRUCTURAS
ALGEBRÁICAS
ÁLGEBRA LINEAL

2. CONCEPTO
• En matemáticas, una estructura algebraica es un
conjunto de elementos con unas propiedades
operacionales determinadas; es decir, lo que
define a la estructura del conjunto son las
operaciones que se pueden realizar con los
elementos de dicho conjunto y las propiedades
matemáticas que dichas operaciones poseen. Un
objeto matemático constituido por un conjunto
no vacío y algunas leyes de composición interna
definida en él es una estructura algebraica.

3. • Para poder comenzar a enumerar las diferentes
estructuras, en primer lugar hay que distinguir entre dos
tipos de operaciones:
a) Operación interna: se llama operación interna en un
conjunto A, a la operación que hace corresponder a
cada par de elementos de AxA con un único elemento
de A.
b) Operación externa:: se llama operación externa en un
conjunto A sobre otro conjunto K, a la operación que
hace corresponder a todo par de elementos (a,k) de AxK
un único elemento de A.

5. • Dentro de las estructuras algebraicas más
importantes que se van a tratar en esta unidad,
están:
• 1. las que tienen una operación interna
• 2. las que tienen dos operaciones internas
• 3. las que tienen una operación interna y otra
externa.

6. ESTRUCTURAS ALGEBRAICAS CON UNA
OPERACIÓN INTERNA
• -Semigrupo: Se dirá que A es un semigrupo, si (A,*) cumple la
propiedad asociativa: si para todo a,b y c pertenecientes a A,
se tiene que (a*b)*c=a*(b*c). Si además se cumple la
propiedad conmutativa: a*b=b*a, entonces se dirá que (A,*)
es un semigrupo conmutativo.
-Monoide: Si (A,*) es un semigrupo que además tiene elemento
neutro que se denota por e:
a*e=e*a=a.
• Por ejemplo el conjunto de los números naturales menos el
cero, con la operación suma, es un semigrupo conmutativo.
Mientras que el conjunto de los números naturales (incluido el
cero) con la operación producto es un monoide.

7. • -Grupo: Se dirá que G es un grupo si (G,*) cumple
las siguientes propiedades: asociativa, existencia
de elemento neutro y existencia de elemento
simétrico o inverso que se denota por i: a*i=i*a=e.
•
-Grupo conmutativo o abeliano: Si (G,*) es un
grupo que cumple además la propiedad
conmutativa.

8. ESTRUCTURAS ALGEBRAICAS CON DOS
OPERACIONES INTERNAS
• Aquí se tienen dos operaciones internas,
que se denotarán a cada una de ellas con
los símbolos * y °.

9. SEMIANILLO
• -Se dirá que (A,*,°) es un semianillo si se cumple que:
1) (A,*) es un monoide, es decir, un semigrupo conmutativo con
elemento neutro.
2) (A, °) es un semigrupo.
3) Se cumple la distributividad de ° respecto de * :
a°(b*c)=(a°b)*(a°c).
-Semianillo conmutativo: Si (A,*, °) es un semianillo y (A,°) es un
semigrupo conmutativo.
Si además tiene elemento neutro, entonces (A, *,°) es
un semianillo conmutativo con elemento unidad.
• Por ejemplo, el conjunto de los números naturales, con las
operaciones suma y producto es un semianillo conmutativo con
elemento unidad: el cero, 0.

10. ANILLO
• Se dirá que (A,*, °) es un anillo, si se cumple que:
1) (A,*) es un grupo conmutativo.
2) (A, °) es un semigrupo.
3) Se cumple la distributividad de ° respecto de *.
Al igual que en el caso de semianillo, si (A, °) es un
semigrupo conmutativo, entonces (A, *, °) es un anillo
conmutativo, y si además tiene elemento neutro,
entonces es un anillo conmutativo con elemento neutro.
• Por ejemplo, el conjunto de los números enteros, los
racionales, los reales y los complejos con las operaciones
suma y producto son anillos conmutativos con elemento
unidad.

11. CUERPO
• -Se llama cuerpo a la terna (K,*, °) que
cumple:
1) (K,*, °) es un anillo
2)(K-{0},°) es un grupo.
Si además (K-{0},°) es un grupo
conmutativo, entonces diremos que (K, *, °)
es un cuerpo conmutativo.

12. ESTRUCTURAS ALGEBRAICAS CON UNA
OPERACIÓN INTERNA Y OTRA EXTERNA
•Por último, se va a a conocer la
estructura algebraica más
importante que tiene una
operación interna * y otra externa,
que se denotará por ●, y se
utilizará como subíndice el
conjunto al que hace referencia.

13. ESPACIO VECTORIAL
• -Se dirá que (V,*v,●k) es un espacio vectorial si
cumple
1) Si (K, *, ●) es un cuerpo.
2) (V, *) es un grupo conmutativo.
3) Se cumple la propiedad distributiva de ● sobre
* por ambos lados.
4) Se cumple la propiedad pseudoasociativa:
a●(b*c)=(a●b)●c
5) Existe elemento unidad.