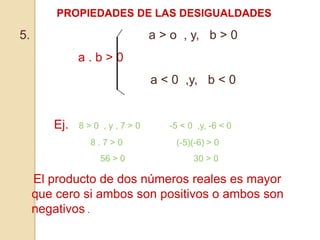
Este documento proporciona una introducción a las desigualdades y los intervalos. Explica las diferentes simbologías de las desigualdades como >, <, ≥ y ≤. Luego describe las propiedades de las desigualdades como la adición, sustracción, multiplicación y división de términos. Finalmente, introduce los diferentes tipos de intervalos como cerrados, abiertos y semiabiertos, y cómo representarlos gráficamente. El documento incluye ejemplos para ilustrar cada concepto.

1. CALCULO
DESIGUALDADES E INTERVALOS

2. CLASIFICACIÓN DE LOS
NÚMEROS

3. DESIGUALDADES
Una desigualdad es una expresión
algebraica relacionada por signos. Nos
sirve para establecer la relación entre dos
cantidades semejantes mediante la siguiente
simbología.
Símbolo>
Significado
Ejemplo
=
Igual
a=3
≠
Diferente
3≠ 3.333
>
Mayor que
π>3
<
Menor que
-1< 0
≥
Mayor o igual que a ≥ b
≤
Menor o igual que X

4. RELACION DE ORDEN ENTRE LOS
NUMEROS REALES
Si a, b Є R
i) a < b sí y solo sí, b - a es positivo. Ej. -10 < -6 → -6 -(-10) = 4
3 <5→5–3=2
ii) a> b sí y solo sí, a – b es positivo Ej. 7 > 2 → 7 – 2 = 5
-2 > -7 → -2 – (-7) =5
Si a,b Є R
i) a ≤ b si y solo si a < b , o bien, a = b
ii) a ≥ b si y solo si a > b, o bien, a = b

5. PROPIEDADES DE LAS DESIGUALDADES
1. Si a < b y c < d → a + c < b + d.
Ej.
2<5
7 < 10
2 + 7 < 5 + 10
Si a > b y c > d → a + c > b + d
Ej
-3 > -5
4>1
-3 + 4 > -5 + 1
Si dos desigualdades del mismo sentido se
suman miembro a miembro la desigualdad no
cambia de sentido.

6. PROPIEDADES DE LAS DESIGUALDADES
2. Si a < b , c Є R → a
c<b
c
Ej. - 4 < 7
- 4 + 2,5 < 7 + 2,5
-1,5 < 9,5
Si a > b , c Є R → a
c>b
c
Ej. 3 > -1
3 – 5 > -1 – 5
-2 > -3
Si sumamos o restamos un mismo número real a
ambos miembros de la desigualdad, la desigualdad
resultante no cambia de sentido.

7. PROPIEDADES DE LAS DESIGUALDADES
3. Si a < b , c > 0 → a.c < b.c , y,
Ej. 4 < 10
a/c < b/c
4 < 10
4 . 2 < 10. 2
4/2 < 10/2
8 < 20
2 < 5
Si a > b , c > 0 → a.c > b.c ,y, a/c > b/c
Ej. 15 > 9
15 . 3 > 9 . 3
45 > 27
15 > 9
15/3 > 9/3
5 > 3
Si se multiplica o divide a ambos miembros de una
desigualdad por un número real positivo la
desigualdad resultante no cambia de sentido.

8. PROPIEDADES DE LAS DESIGUALDADES
4. Si a < b , y, c < 0 → a . c > b . c ,y, a/c > b/c
Ej.
3 < 12
3 < 12
3 (-3) > 12 (-3)
3 / (-3) > 12/ (-3)
-9
>
-36
-1 > -4
Si a > b , y, c < 0 → a . c < b . c , y, a/c < b/c
Ej.
3 > -4
3 (-2) < -4 (-2)
-6 < 8
3 > -4
3 / (-2) < (-4) / (-2)
-3/2 < 2
Si se multiplica o divide a ambos miembros de una
desigualdad por un número real negativo, la
desigualdad resultante cambia de sentido.

9. PROPIEDADES DE LAS DESIGUALDADES
5.
a > o , y, b > 0
a.b>0
a < 0 ,y, b < 0
Ej.
8>0 ,y,7>0
-5 < 0 ,y, -6 < 0
8.7>0
(-5)(-6) > 0
56 > 0
30 > 0
El producto de dos números reales es mayor
que cero si ambos son positivos o ambos son
negativos .

10. INTERVALO DE UNA VARIABLE
Es el conjunto de valores que puede
tomar la variable dependiente y que
están comprendidos entre dos de
ellos: a y b, que se denominan
extremos del intervalo.
 La diferencia que existe entre ambos
extremos se conoce como Amplitud
de intervalo y es igual al valor
absoluto de su diferencia |a-b|


11. INTERVALO DE UNA VARIABLE
Notación de intervalo:
[a,b]
“intervalo de a hacia b”
Notación para la variable:
a<x<b
“la variable x es mayor que a y
menor que b”

12. CLASIFICACIÓN DE
INTERVALOS
INTERVALO
¿QUE REPRESENTA?
CERRADO
[a,b]
{x|a≤x≤b}
ABIERTO
(a,b)
{x|a<x<b}
SEMIABIERTO POR LA
IZQUIERDA
(a,b]
{x|a<x≤b}
SEMIABIERTO POR LA
DERECHA
[a,b)
{x|a≤x<b}
INFINITO
(a,+ œ) , [a,+ œ)
(-œ,b) , (-œ,b]

13. Representación gráfica de los
intervalos

En la recta real los valores a y b se
denominan extremos del intervalo

Resolver una desigualdad significa
encontrar todas sus soluciones, es
decir obtener el intervalo donde la
relación es verdadera.

14. DESIGUALDADES.
EJEMPLO 1:
 Encuentra el conjunto de solución que satisfaga la
siguiente desigualdad:


15. Ejemplo 2

16. Ejemplo 3 Doble desigualdad

17. Ejemplo 4: Desigualdad cuadrática

18. Ejemplo 5: Desigualdad de racionales

19. EJERCICIO 1Resuelve las siguientes inecuaciones o
desigualdades e indica su intervalo
1
3x < 15
12
7> 8x - 5
2
3x + 6 > 2x + 12
13
1 - 5x < -8
3
4x - 8 > 3x – 14
14
x–3 < 3-x
4
10x + 24 < 16x + 12
15
3x + 5 ≥ 4x-1
5
- 2x + 3 > - 3x – 1
16
2x+ 5>6x+4
6
5(x + 6) - 5 > - 10
17
3x + 7 ≥ 2x-3
7
6 + 3(x + 1) > 7 + 4(x - 1)
18
- 4x + 9 < x - 1
8
5 - [ 2x + (x + 2) ] < 4
19
3x - 1 ≥ x - 3
9
2x+ 4 > 0
20
3x - 1 ≤ 2x+1
10
3x - 7< 5
21
x + 2 ≤ 3x - 5
4
11
2 - x >3