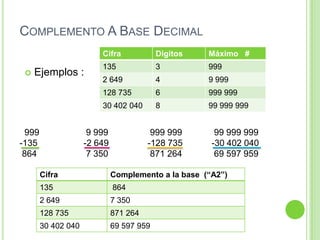
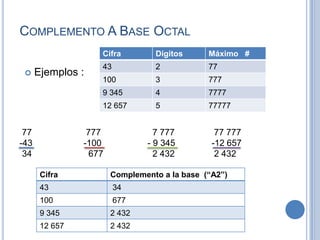
El documento explica cómo calcular el complemento a la base de un número en diferentes sistemas de numeración. Para calcular el complemento a la base de un número, se toma en cuenta la cantidad de dígitos del número, se forma el número máximo posible con esa cantidad de dígitos según el sistema, y luego se resta este número máximo del número original. Esto permite representar números negativos de una manera que simplifica las operaciones aritméticas en los sistemas binario, octal y decimal.

1. INSTITUTO TECNOLÓGICO DE COSTA RICA
ESCUELA DE COMPUTACIÓN
COMPLEMENTOS A UNA BASE NUMÉRICA
Fabián Zúñiga Vásquez.
Taller de Programación
Noviembre 2013

2. COMPLEMENTOS A UNA BASE NUMÉRICA

Muchas computadoras digitales utilizan un sistema numérico de
complemento a base a fin de minimizar la cantidad de circuitos
necesarios para realizar la aritmética de enteros.

Por ejemplo, se puede realizar la operación : A - B calculando
A + (- B), donde (- B) está representado por el complemento a la
base de B. Por tanto, la computadora sólo necesita un sumador
binario y algunos circuitos complementarios para la suma y la resta.

Sin embargo el complemento a la base se puede aplicar no solo al
sistema numérico binario, otros formatos también poseen dicho
complemento.

A continuación se muestra un breve resumen de esto.

3. COMPLEMENTOS A LA BASE


Si se desea complementar a la
base una cifra de “n” dígitos
tome dicha cantidad de dígitos y
forme el máximo numero
posible para ese sistema
numérico
con
dicha
cantidad, esto es:
Considere:
Cifra= 75
n=2 (cant. dígitos en 75)
*Max # = 99

99
-75
24c

(Pues en *sistema decimal10 el 9
es el mayor numero alcanzable
con un solo dígito )
Luego de formar el máximo
numero posible debemos de
restarle a este la cifra
original que queremos
complementar, de la
siguiente manera :

Max # posible
Cifra original
Complemento de
la cifra original
De esta forma obtenemos
que 75 en complemento a la
base es igual a 22.
7510=22c

4. COMPLEMENTO A BASE DECIMAL
Cifra
999
-135
864
135
3
999
2 649
4
9 999
6
999 999
30 402 040
Ejemplos :
Máximo #
128 735

Dígitos
8
99 999 999
9 999
-2 649
7 350
999 999
-128 735
871 264
99 999 999
-30 402 040
69 597 959
Cifra
Complemento a la base (“A2”)
135
864
2 649
7 350
128 735
871 264
30 402 040
69 597 959

5. COMPLEMENTOS A LA BASE


Se aplica de igual forma que en
el sistema decimal:
Considere ahora :
Cifra= 01112 (7d)
n=4 (cant. dígitos en 0111)
Max # = 11112 (15d)
(Pues en *sistema binario2 el 1 es
el mayor numero alcanzable
con un solo dígito )

Y se procede a la resta* :
1111
- 0111
1000c
Max # posible
Cifra original
Complemento de
la cifra original

De esta forma obtenemos
que 01112 en complemento a
la base es igual a 10002.
01112=1000c2

Que en decimal seria :

15-7=8, siendo 8 el
complemento


6. COMPLEMENTO A BASE BINARIA
Cifra
11111
-10101
01010
10101
5
11 111
100
3
111
7
111111
10011
Ejemplos :
Máximo #
1110101

Dígitos
5
11111
111
-100
011
1111111
-1110101
0001010
11111
-10011
01100
Cifra
Complemento a la base (“A2”)
10101
01010
100
011
1110101
0001010
10011
01100

7. COMPLEMENTOS A LA BASE


Se
utiliza
el
procedimiento que
métodos anteriores :
mismo
en los
Considere ahora :
Cifra= 3278
n=3 (cant. dígitos en 327)
Max # = 7778
(Pues en *sistema octal8 el 7 es el
mayor numero alcanzable con
un solo dígito )

Y se procede a la resta* :
777
- 327
450c


Max # posible
Cifra original
Complemento de
la cifra original
De esta forma obtenemos
que 3278 en complemento a
la base es igual a 450.
3278=450c8

8. COMPLEMENTO A BASE OCTAL
Cifra
77
-43
34
43
2
77
100
3
777
4
7777
12 657
Ejemplos :
Máximo #
9 345

Dígitos
5
77777
777
-100
677
7 777
- 9 345
2 432
77 777
-12 657
2 432
Cifra
Complemento a la base (“A2”)
43
34
100
677
9 345
2 432
12 657
2 432

9. COMPLEMENTOS A LA BASE
Para base 4:
Para base 9:
Cifra
Dígitos
Máximo #
Cifra
Dígitos
Máximo #
223
3
333
74023
5
88888
1210
4
3333
62
2
88
333
-223
110
3333
-1210
2123
88 888
-74023
14865
88
-62
26

10. CONCLUSIÓN
1.
2.
3.
PARA 124310
Para complementar a la base una cifra de cualquier sistema
de numeración:
Tome en cuenta los dígitos de la cifra, (n=4).
Utilice la cantidad de dígitos para formar el mayor numero
posible según
el sistema numérico que se esta
usando, (9999).
Reste el numero recién formado con la cifra original.
999910-124310= 875410
4.
El numero obtenido de la resta es el complemento de la cifra
original
De esta forma, en este ultimo ejemplo 8754 es el
complemento de 1243 para el sistema decimal.

11. NOTAS

Sistema decimal10 = {0,1,2,3,4,5,6,7,8,9}

Sistema octal8 = {0,1,2,3,4,5,6,7}

Sistema binario2 ={0,1}

Max # = numero máximo que se puede crear(en estos
casos seria el ultimo numero utilizable de cada sistema
(n-1)).