Este documento describe las características y la cinemática del robot KUKA KR 6-2. Presenta las especificaciones técnicas del robot, incluyendo su espacio de trabajo y parámetros de articulación. Explica el modelo cinemático directo utilizando la tabla de parámetros de Denavit-Hartenberg y matrices de transformación homogénea para calcular la posición del efector final basada en los valores de las articulaciones.

![Din´amica de Robots
Caracter´ısticas del Robot
Cinem´atica
Simulaciones
Bibliograf´ıa
Caracter´ısticas t´ecnicas
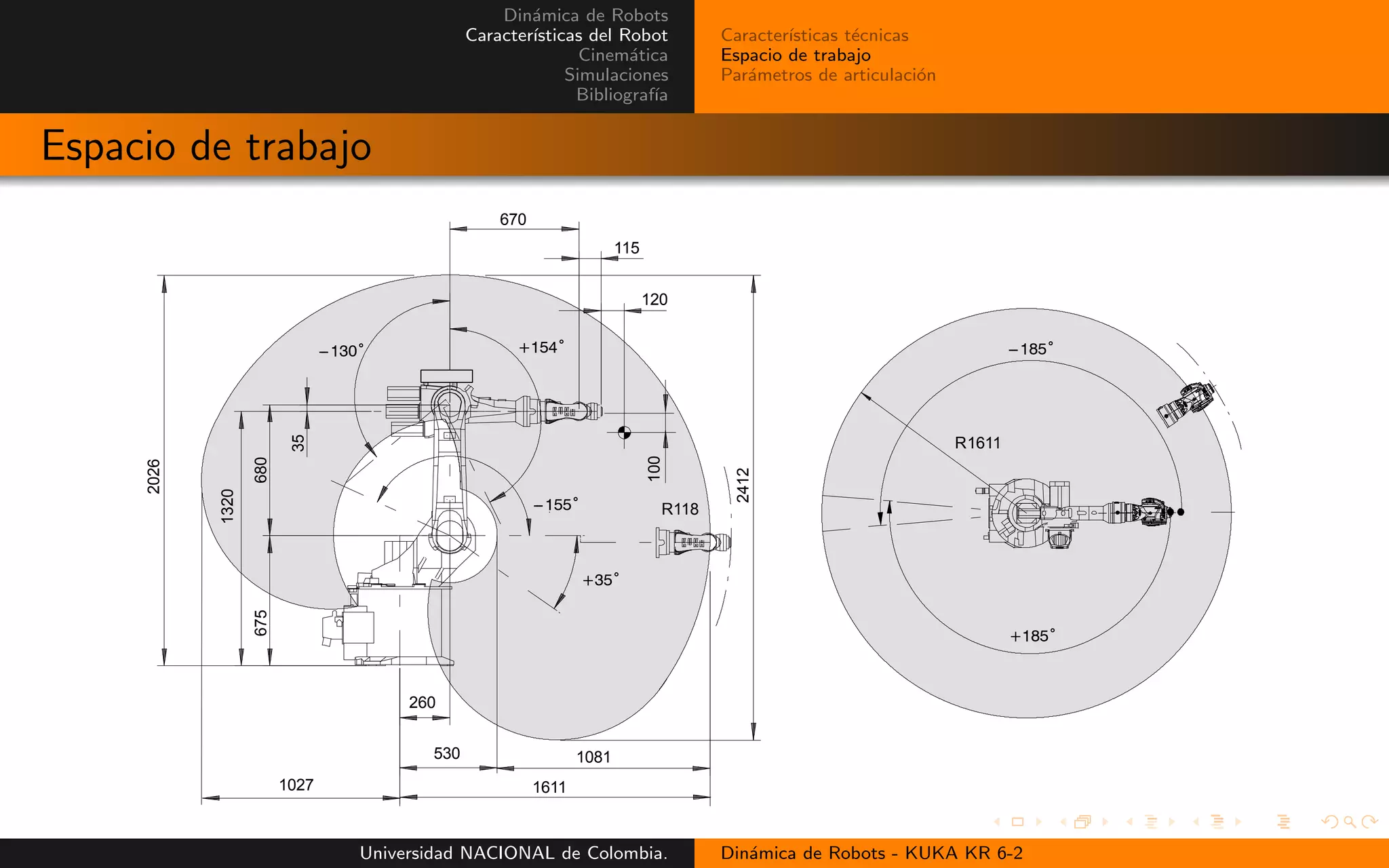
Espacio de trabajo
Par´ametros de articulaci´on
Descripci´on del Robot
´Item Descripci´on
Carga ´util nominal 6[kg]
Carga en el brazo 10[kg]
Carga en el eslab´on del
brazo
variable
Carga en la columna de ro-
taci´on
20[kg]
Carga distribuida total 36[kg]
Carga distribuida total 36[kg]
El robot KR 6, es un robot de 6
grados de libertad de juntas de
revoluci´on optimizado para las
siguientes tareas:
Manipulaci´on.
Ensamblaje.
Aplicaci´on de adhesivos y
sellantes .
Maquinado.
Universidad NACIONAL de Colombia. Din´amica de Robots - KUKA KR 6-2](https://image.slidesharecdn.com/dinamicaderobots-sierrasierranelsonariel-kuka-kr6-2-130924231741-phpapp01/75/Estudio-de-Robot-KUKA-KR-6-2-2048.jpg)
![Din´amica de Robots
Caracter´ısticas del Robot
Cinem´atica
Simulaciones
Bibliograf´ıa
Caracter´ısticas t´ecnicas
Espacio de trabajo
Par´ametros de articulaci´on
Caracter´ısticas del Robot
Eje Posici´on Velocidad
1 ±185[◦] 156[◦/s]
2 -125 a 65 [◦] 156[◦/s]
3 15 a -130 [◦] 156[◦/s]
4 ±350[◦] 343[◦/s]
5 ±130[◦] 362[◦/s]
6 ±350[◦] 659[◦/s]
´Angulos tomados desde la posici´on “Home”del Robot.
Universidad NACIONAL de Colombia. Din´amica de Robots - KUKA KR 6-2](https://image.slidesharecdn.com/dinamicaderobots-sierrasierranelsonariel-kuka-kr6-2-130924231741-phpapp01/75/Estudio-de-Robot-KUKA-KR-6-3-2048.jpg)

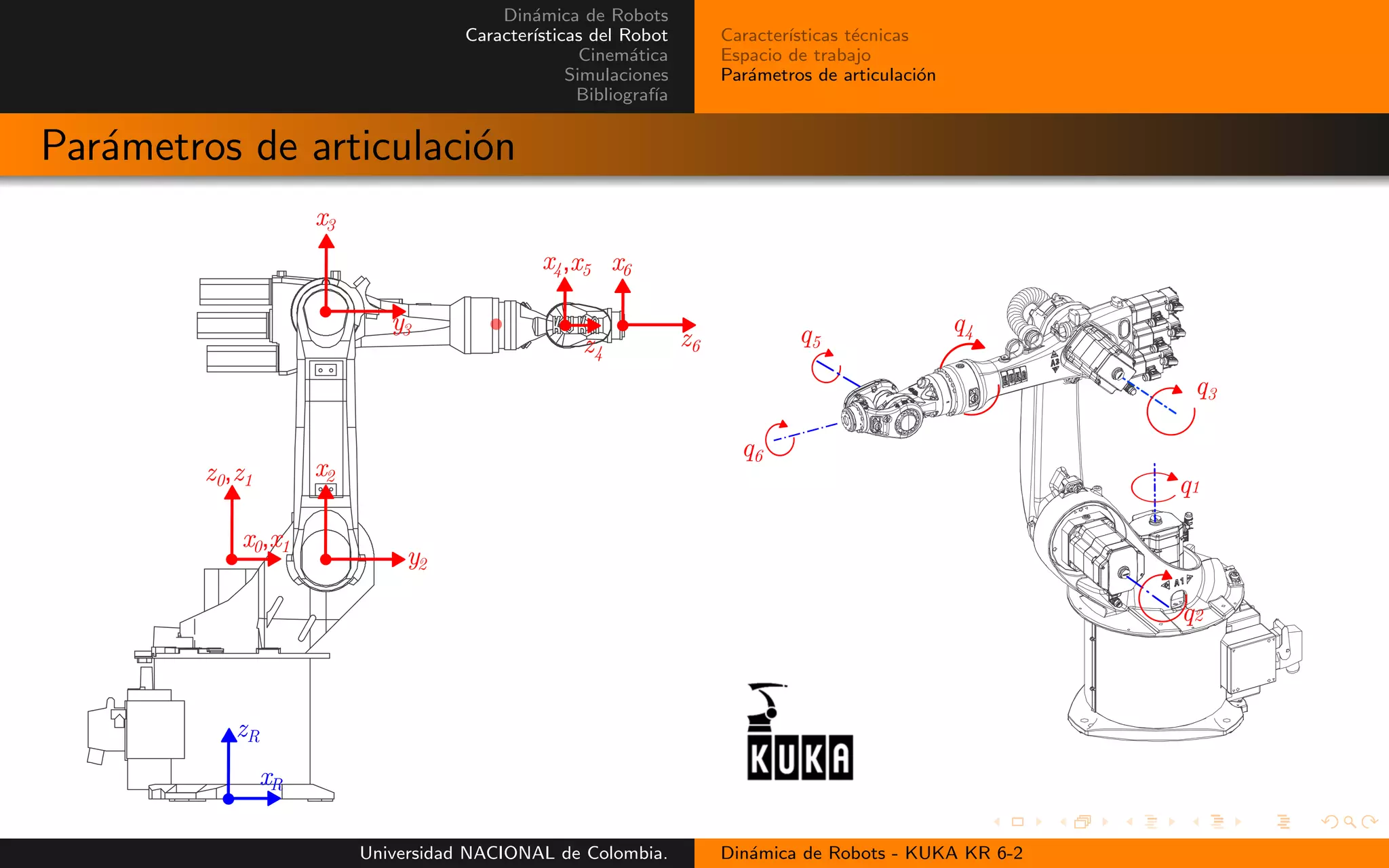

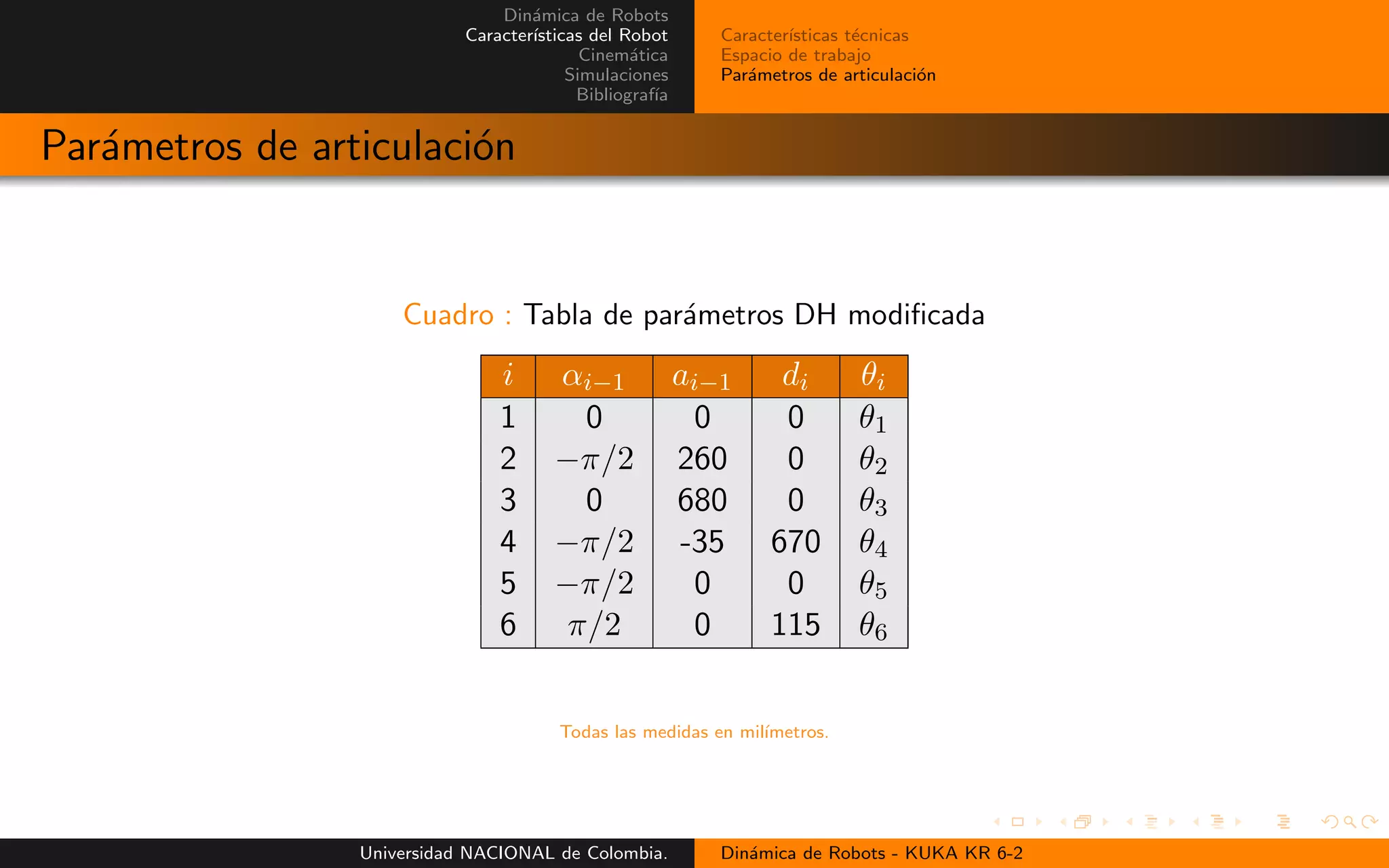




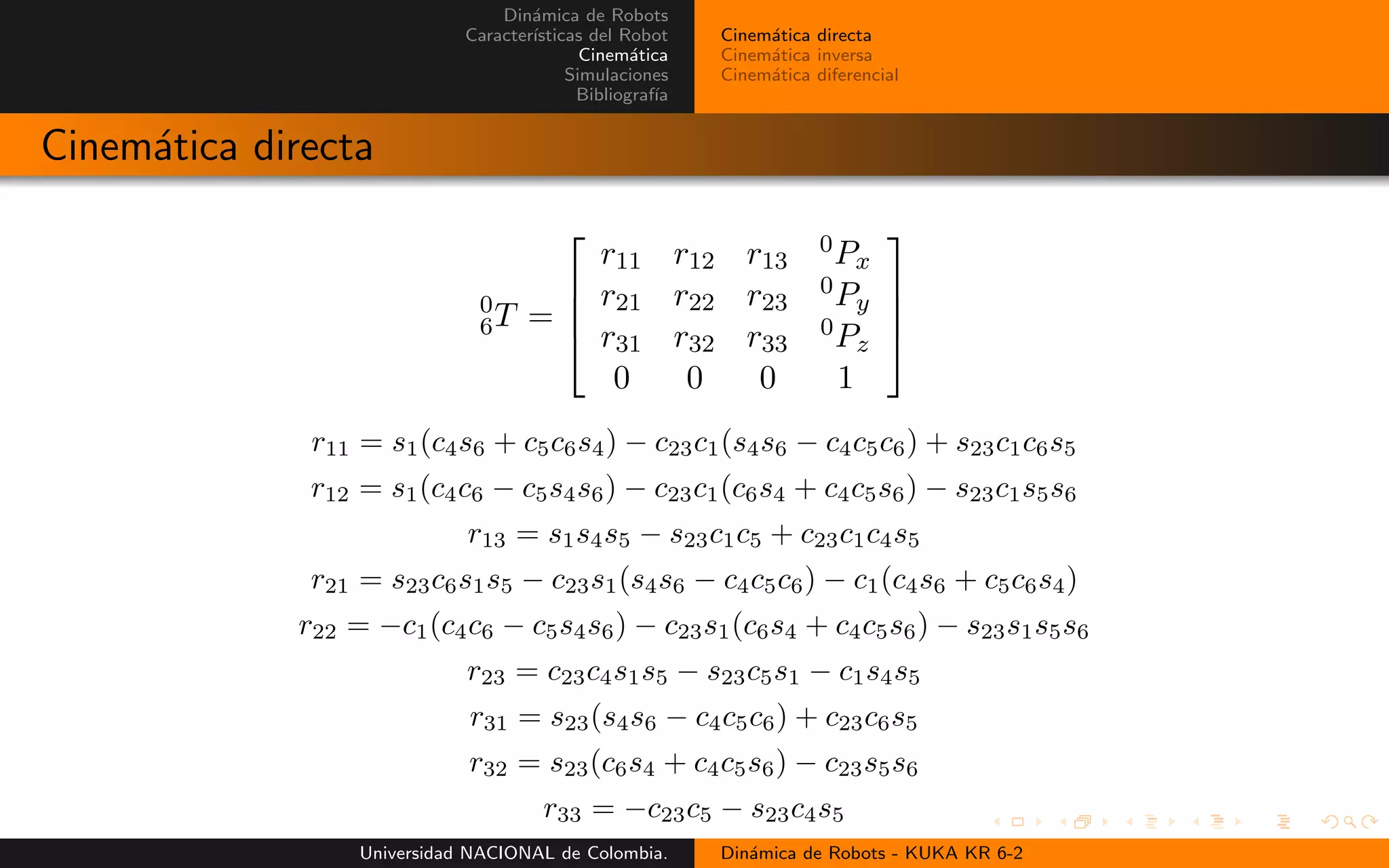


![Din´amica de Robots
Caracter´ısticas del Robot
Cinem´atica
Simulaciones
Bibliograf´ıa
Cinem´atica directa
Cinem´atica inversa
Cinem´atica diferencial
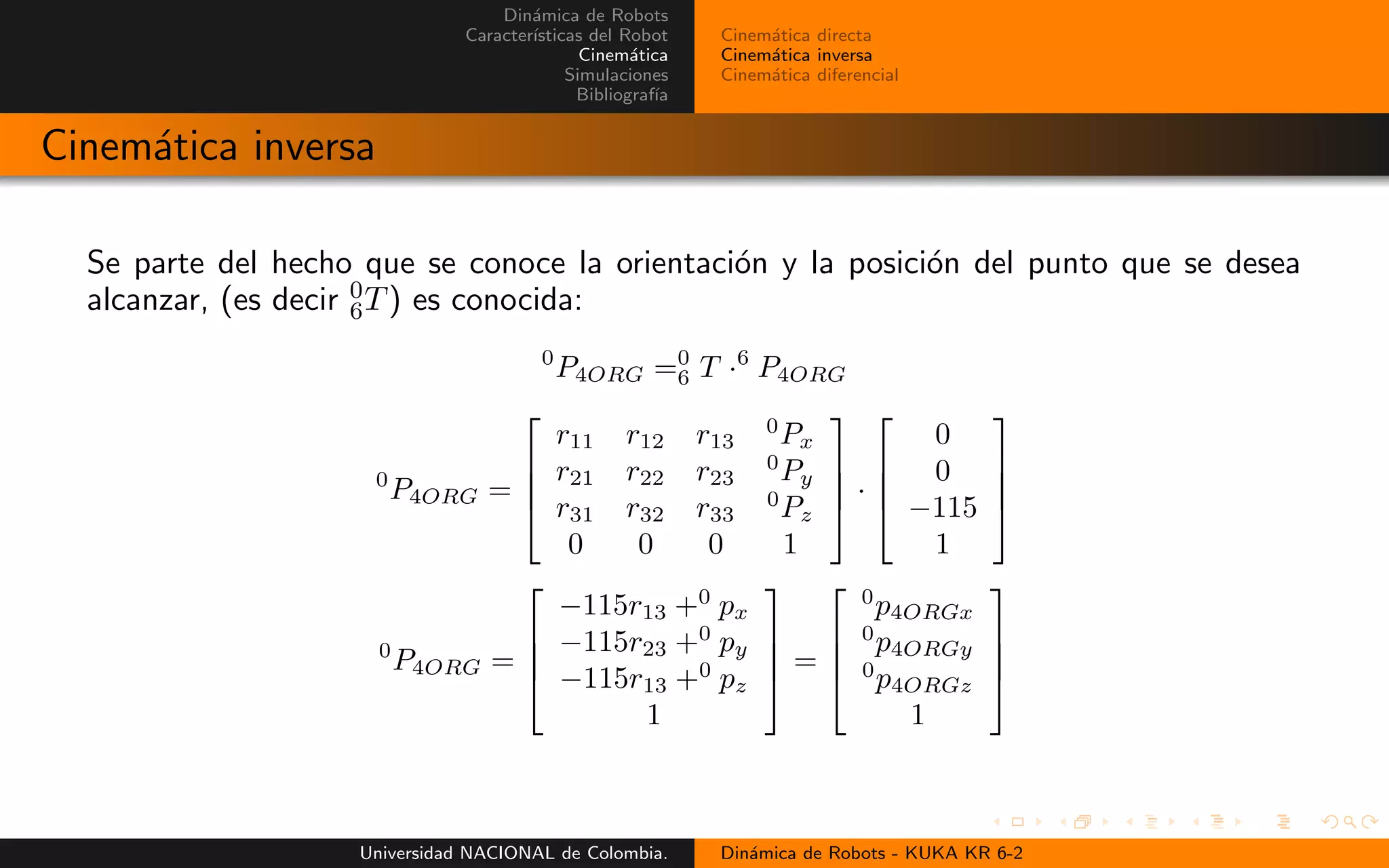
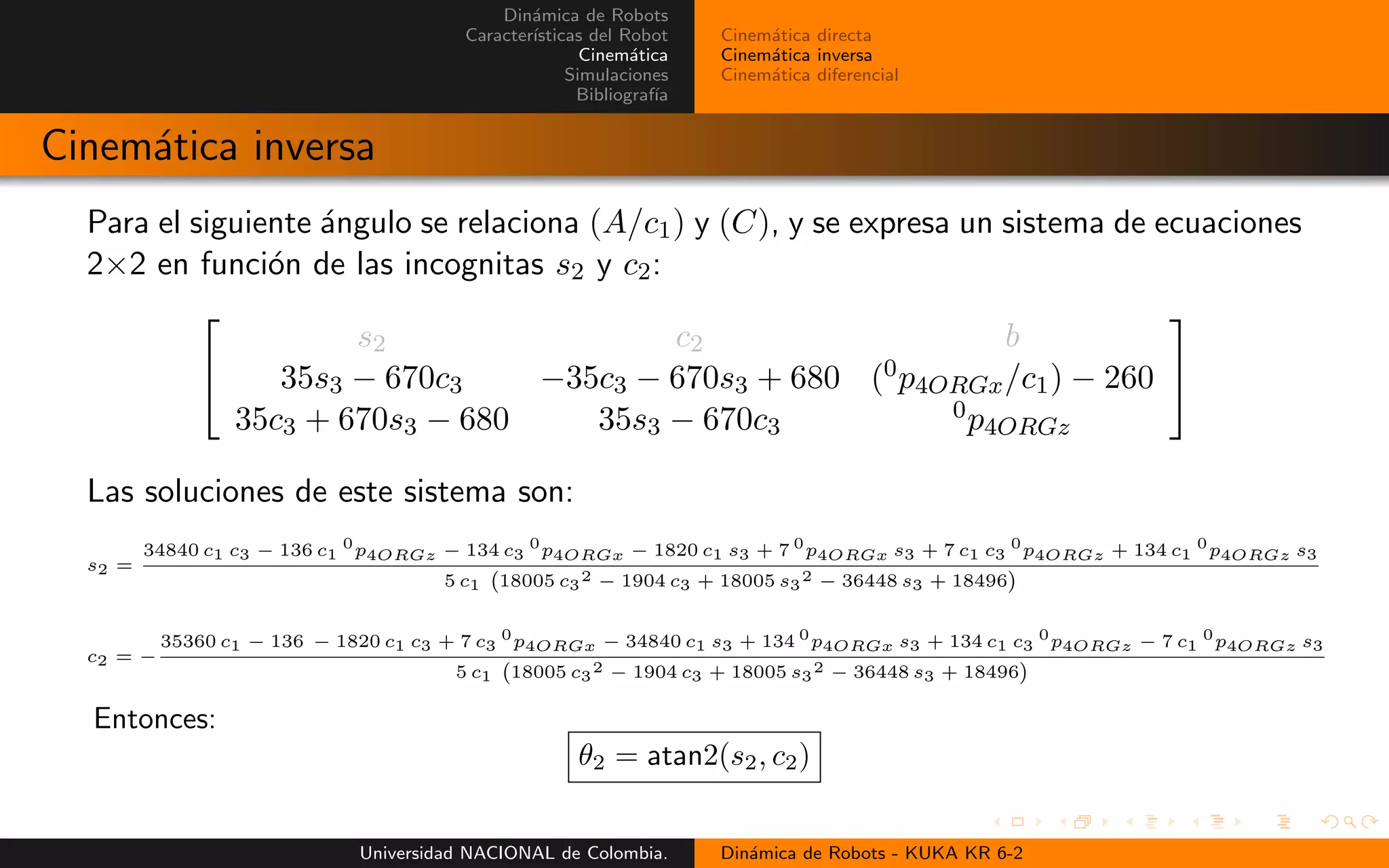
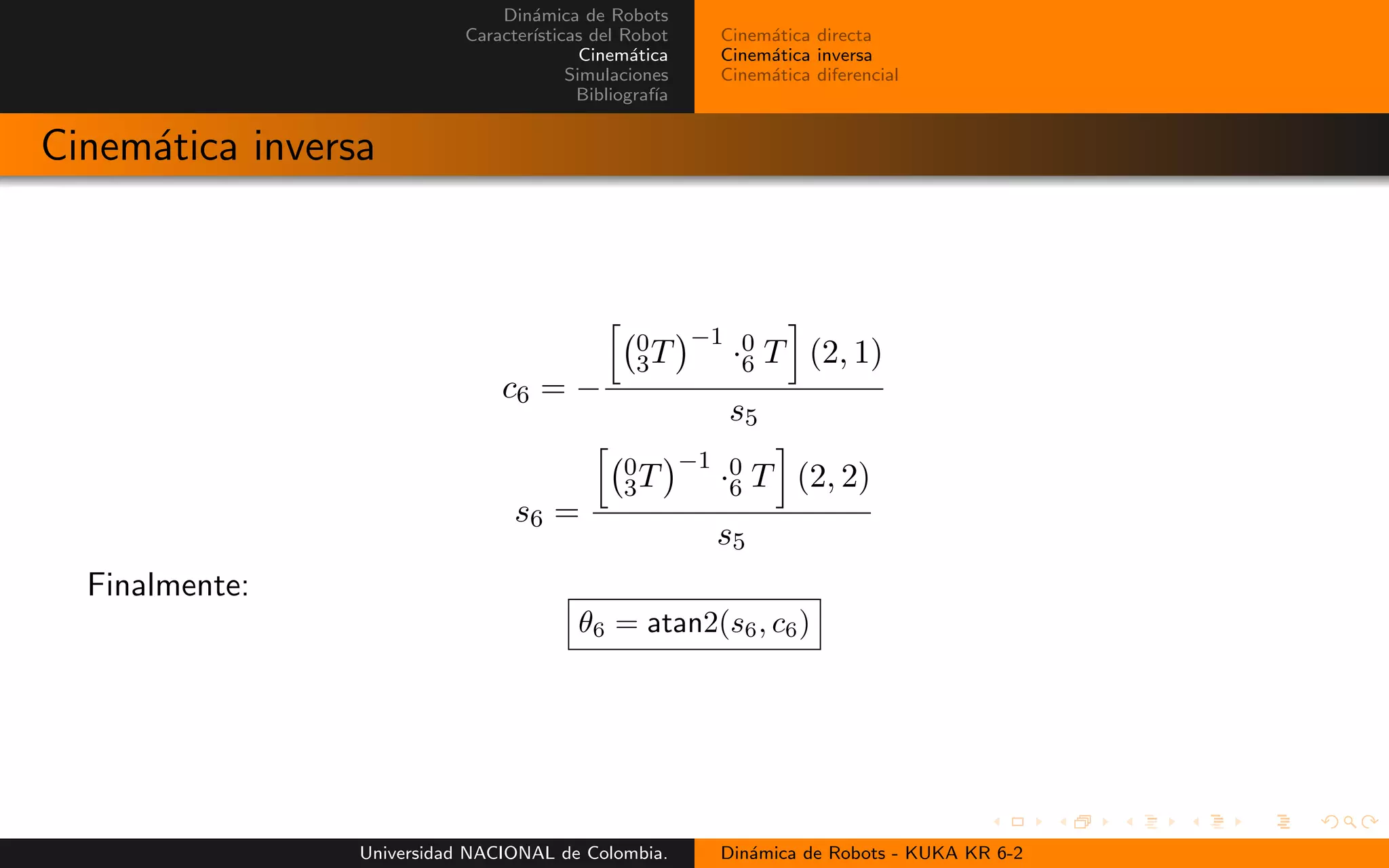
Cinem´atica inversa
A su vez se define como igualdad
0
P4ORG =0
3 T ·3
P4ORG
Al realizar dicha multiplicaci´on:
0
P4ORG =
−35c23c1 − 670s23c1 + 20c1(34c2 + 13)
−35c23s1 − 670s23s1 + 20s1(34c2 + 13)
35s23 − 670c23 − 680s2
1
=
A
B
C
1
=
0
p4ORGx
0
p4ORGy
0
p4ORGz
1
Al realizar la comparaci´on entre A/c1 y B/s1, se obtiene:
[A/c1] ⇒ −35c23 − 670s23 + 20(34c2 + 13) =0
p4ORGx/c1
[B/s1] ⇒ −35c23 − 670s23 + 20(34c2 + 13) =0
p4ORGy/s1
Universidad NACIONAL de Colombia. Din´amica de Robots - KUKA KR 6-2](https://image.slidesharecdn.com/dinamicaderobots-sierrasierranelsonariel-kuka-kr6-2-130924231741-phpapp01/75/Estudio-de-Robot-KUKA-KR-6-17-2048.jpg)








![Din´amica de Robots
Caracter´ısticas del Robot
Cinem´atica
Simulaciones
Bibliograf´ıa
Cinem´atica directa
Cinem´atica inversa
Cinem´atica diferencial
C´alculo del Jacobiano
J46 = s6
J51 = s23c6s4 − s6(c23s5 − s23c4c5)
J52 = s23c6s4 − s6(c23s5 − s23c4c5)
J53 = c5s4s6 − c4c6
J54 = c5s4s6 − c4c6
J55 = s5s6
J56 = c6
J61 = −c23c5 − s23c4s5
J62 = −c23c5 − s23c4s5
J63 = −s4s5
J64 = −s4s5
J65 = c5
150[mm]
Universidad NACIONAL de Colombia. Din´amica de Robots - KUKA KR 6-2](https://image.slidesharecdn.com/dinamicaderobots-sierrasierranelsonariel-kuka-kr6-2-130924231741-phpapp01/75/Estudio-de-Robot-KUKA-KR-6-28-2048.jpg)
![Din´amica de Robots
Caracter´ısticas del Robot
Cinem´atica
Simulaciones
Bibliograf´ıa
Descripci´on de la trayectoria
Gr´aficas de articulaci´on
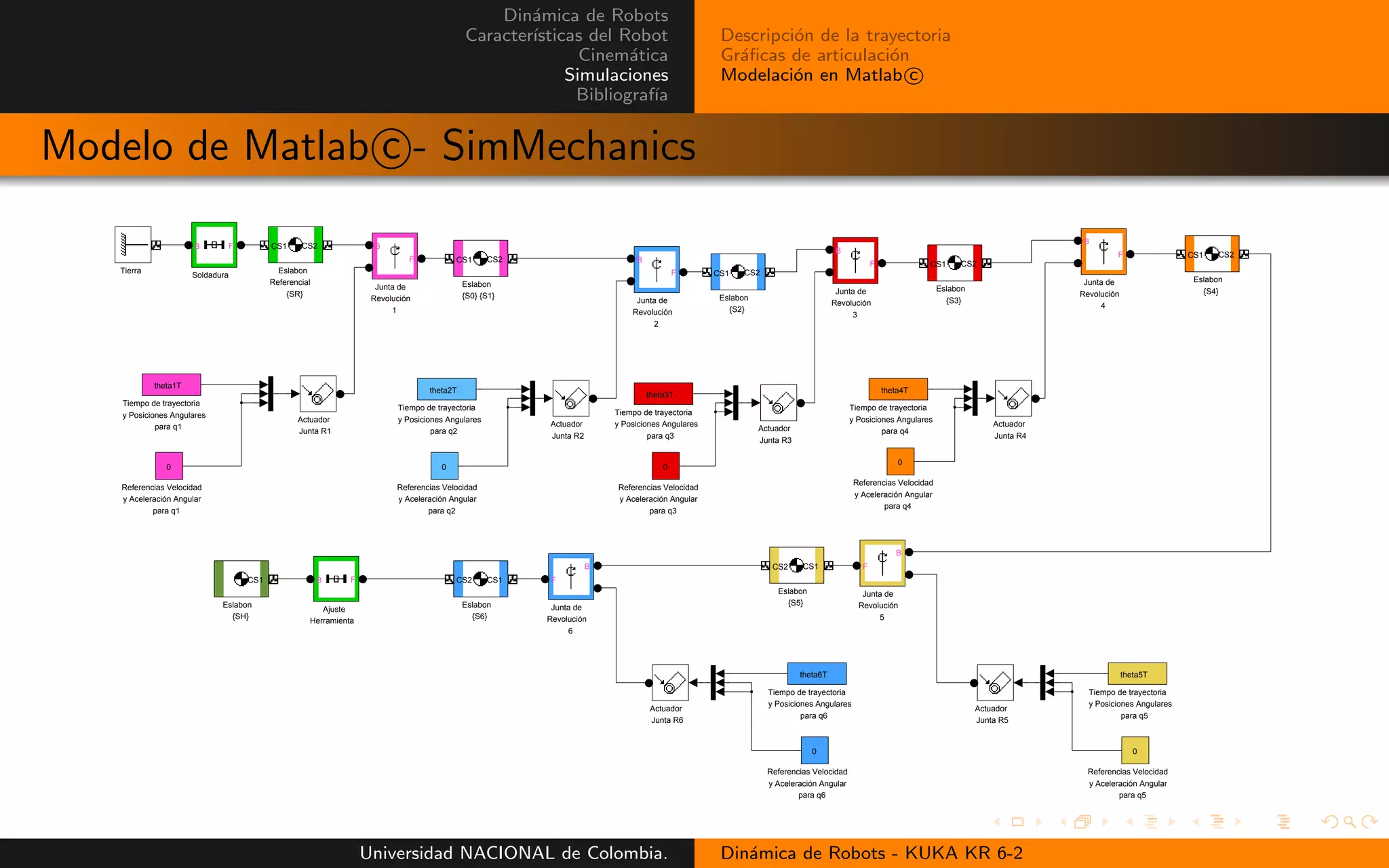
Modelaci´on en Matlab c
Descripci´on de la trayectoria
c1
c2c3
c4
[xp, 350, 400] [xp, 50, 400]
A B
C
D
EF
G
H [xp, 0, 450]
[xp, 0, 550]
[xp, 50, 600][xp, 350, 600]
[xp, 400, 550]
[xp, 400, 450]
[xp, 200, 500]
[xp, 350, 450]
[xp, 350, 550] [xp, 50, 550]
[xp, 50, 450]
zP
xP
12
1113
14
15
10
1
2
3 4
5
6
7
8
9
Dimensiones (400 × 200 × 30)[mm] y Ubicaci´on del centro de la placa = [xP , 200, 500][mm]
Universidad NACIONAL de Colombia. Din´amica de Robots - KUKA KR 6-2](https://image.slidesharecdn.com/dinamicaderobots-sierrasierranelsonariel-kuka-kr6-2-130924231741-phpapp01/75/Estudio-de-Robot-KUKA-KR-6-29-2048.jpg)
![Din´amica de Robots
Caracter´ısticas del Robot
Cinem´atica
Simulaciones
Bibliograf´ıa
Descripci´on de la trayectoria
Gr´aficas de articulaci´on
Modelaci´on en Matlab c
Parametrizaci´on de la trayectoria (Desplazamiento)
[A-B] (y decrece)
z = 450
(B-C] (y decrece)
z = − 502 − (y − c1(y))2 + c1(z)
(C-D] (z crece)
y = 0
(D-E] (y crece)
z = 502 − (y − c2(y))2 + c2(z)
(E-F] (y crece)
z = 600
(F-G] (y crece)
z = 502 − (y − c3(y))2 + c3(z)
(G-H] (z decrece)
y = 400
(H-A] (y decrece)
z = − 502 − (y − c4(y))2 + c4(z)
Universidad NACIONAL de Colombia. Din´amica de Robots - KUKA KR 6-2](https://image.slidesharecdn.com/dinamicaderobots-sierrasierranelsonariel-kuka-kr6-2-130924231741-phpapp01/75/Estudio-de-Robot-KUKA-KR-6-30-2048.jpg)

![Din´amica de Robots
Caracter´ısticas del Robot
Cinem´atica
Simulaciones
Bibliograf´ıa
Descripci´on de la trayectoria
Gr´aficas de articulaci´on
Modelaci´on en Matlab c
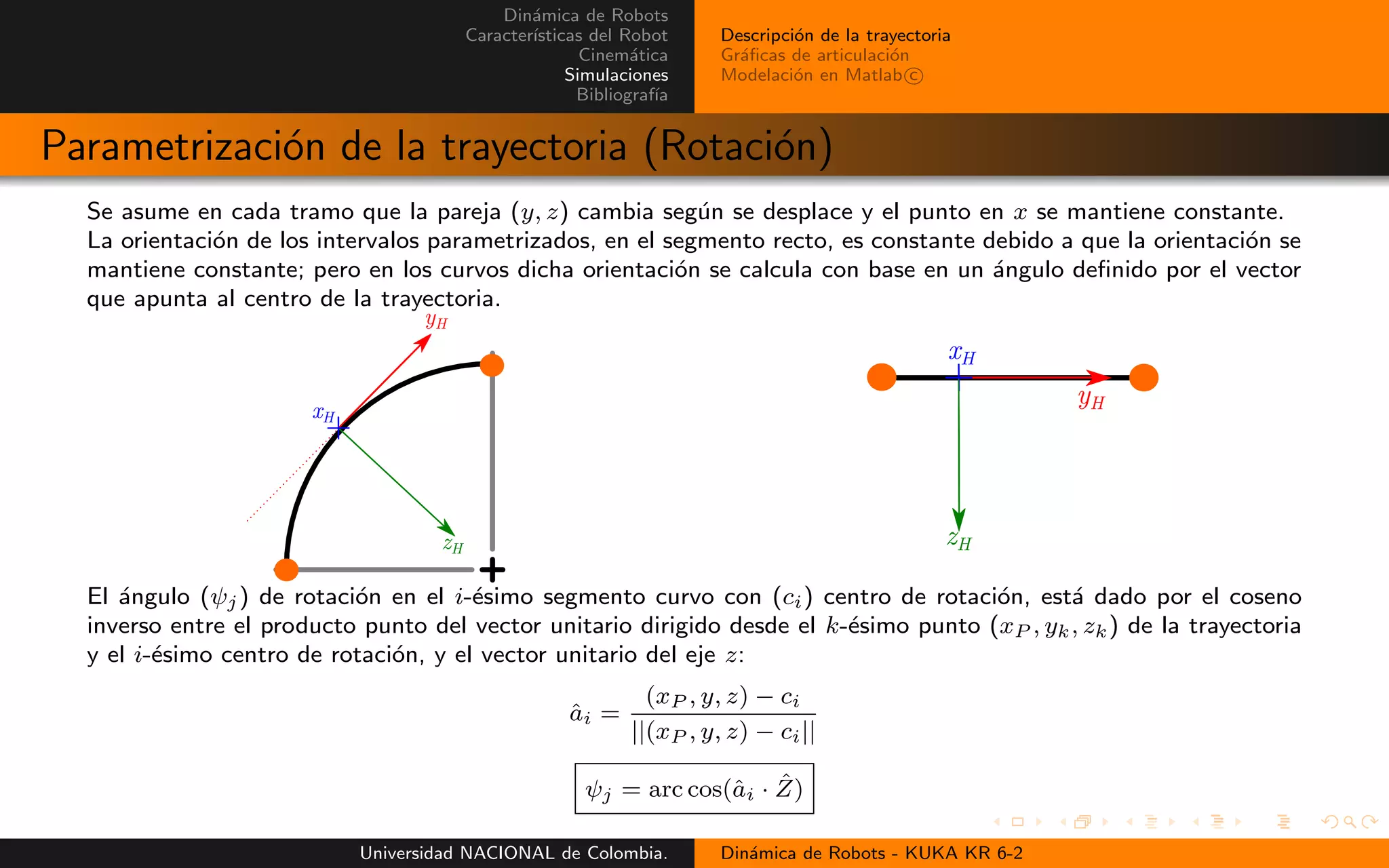
Parametrizaci´on de la trayectoria (Rotaci´on)
Trayectoria [A-B]:
0
H R = Ry(π/2) · Rz(π)
Trayectoria (B-C]:
.
.....El ´angulo ψ cambia, ya que se eval´ua en cada iteraci´on, entre los l´ımites:
Cambia de (ψ1 = 0) a (ψ1 = −π/2)
0
H R = Ry(π/2) · Rz(π) · Rx(ψ1)
Trayectoria (C-D]:
0
H R = Ry(π/2) · Rz(π) · Rx(−π/2)
Trayectoria (D-E]:
.
.....El ´angulo ψ cambia, ya que se eval´ua en cada iteraci´on, entre los l´ımites:
Cambia de (ψ2 = −π/2) a (ψ2 = −π)
0
H R = Ry(π/2) · Rz(π) · Rx(ψ2)
Universidad NACIONAL de Colombia. Din´amica de Robots - KUKA KR 6-2](https://image.slidesharecdn.com/dinamicaderobots-sierrasierranelsonariel-kuka-kr6-2-130924231741-phpapp01/75/Estudio-de-Robot-KUKA-KR-6-33-2048.jpg)
![Din´amica de Robots
Caracter´ısticas del Robot
Cinem´atica
Simulaciones
Bibliograf´ıa
Descripci´on de la trayectoria
Gr´aficas de articulaci´on
Modelaci´on en Matlab c
Parametrizaci´on de la trayectoria (Rotaci´on)
Trayectoria (E-F]:
0
H R = Ry(π/2) · Rz(π) · Rx(−π)
Trayectoria (F-G]:
.
.....El ´angulo ψ cambia, ya que se eval´ua en cada iteraci´on, entre los l´ımites:
Cambia de (ψ3 = −π) a (ψ3 = −3π/2)
0
H R = Ry(π/2) · Rz(π) · Rx(ψ3)
Trayectoria (G-H]:
0
H R = Ry(π/2) · Rz(π) · Rx(−3π/2)
Trayectoria (H-A]:
.
.....El ´angulo ψ cambia, ya que se eval´ua en cada iteraci´on, entre los l´ımites:
Cambia de (ψ4 = −3π/2) a (ψ4 = −2π)
0
H R = Ry(π/2) · Rz(π) · Rx(ψ4)
Universidad NACIONAL de Colombia. Din´amica de Robots - KUKA KR 6-2](https://image.slidesharecdn.com/dinamicaderobots-sierrasierranelsonariel-kuka-kr6-2-130924231741-phpapp01/75/Estudio-de-Robot-KUKA-KR-6-34-2048.jpg)
![Din´amica de Robots
Caracter´ısticas del Robot
Cinem´atica
Simulaciones
Bibliograf´ıa
Descripci´on de la trayectoria
Gr´aficas de articulaci´on
Modelaci´on en Matlab c
Descripci´on de la trayectoria
0 100 200 300 400 500 600 700 800 900 1000
−400
−350
−300
−250
−200
−150
−100
−50
0
Muestras
θ[º]
1199
1199.5
1200
1200.5
1201
0
100
200
300
400
400
450
500
550
600
xy
z
Universidad NACIONAL de Colombia. Din´amica de Robots - KUKA KR 6-2](https://image.slidesharecdn.com/dinamicaderobots-sierrasierranelsonariel-kuka-kr6-2-130924231741-phpapp01/75/Estudio-de-Robot-KUKA-KR-6-35-2048.jpg)
![Din´amica de Robots
Caracter´ısticas del Robot
Cinem´atica
Simulaciones
Bibliograf´ıa
Descripci´on de la trayectoria
Gr´aficas de articulaci´on
Modelaci´on en Matlab c
Gr´aficas de articulaci´on - Velocidad
Las posiciones de articulaci´on se hallan evaluando la parametrizaci´on de posici´on y rotaci´on en la funci´on de
cinem´atica inversa y optimizando tales resultados. Las velocidades se articulaci´on se hallan ayudados por la
definici´on del Jacobiano inverso, tomando en cuenta que ´unicamente en los segmentos curvos existe velocidad
angular y que la velocidad lineal (tangencial) es constante durante toda la trayectoria.
H
vH = [0, −100, 0]T
[mm/s]
p =
2πr
4
=
2π(50)
4
= 25π[mm]
ttrayectoria =
p
v
=
25π
100
=
π
4
[s]
|ωx| =
∆θ
ttrayectoria
=
π/2
π/4
H
ωH = [−2, 0, 0]T
[rad/s]
Universidad NACIONAL de Colombia. Din´amica de Robots - KUKA KR 6-2](https://image.slidesharecdn.com/dinamicaderobots-sierrasierranelsonariel-kuka-kr6-2-130924231741-phpapp01/75/Estudio-de-Robot-KUKA-KR-6-36-2048.jpg)
![Din´amica de Robots
Caracter´ısticas del Robot
Cinem´atica
Simulaciones
Bibliograf´ıa
Descripci´on de la trayectoria
Gr´aficas de articulaci´on
Modelaci´on en Matlab c
Gr´aficas de articulaci´on - Posici´on
0 100 200 300 400 500 600 700 800 900 1000
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
Gráficas de Posición para θ1
θ[rad]
0 100 200 300 400 500 600 700 800 900 1000
−1.3
−1.25
−1.2
−1.15
−1.1
−1.05
−1
−0.95
−0.9
−0.85
Gráficas de Posición para θ2
0 100 200 300 400 500 600 700 800 900 1000
−0.9
−0.8
−0.7
−0.6
−0.5
−0.4
−0.3
−0.2
−0.1
0
0.1
Gráficas de Posición para θ3
0 100 200 300 400 500 600 700 800 900 1000
−4
−3
−2
−1
0
1
2
3
4
Muestras
θ[rad]
Gráficas de Posición para θ4
0 100 200 300 400 500 600 700 800 900 1000
−3.5
−3
−2.5
−2
−1.5
−1
−0.5
0
Gráficas de Posición para θ5
Muestras
0 100 200 300 400 500 600 700 800 900 1000
−4
−3
−2
−1
0
1
2
3
4
Muestras
Gráficas de Posición para θ6
Universidad NACIONAL de Colombia. Din´amica de Robots - KUKA KR 6-2](https://image.slidesharecdn.com/dinamicaderobots-sierrasierranelsonariel-kuka-kr6-2-130924231741-phpapp01/75/Estudio-de-Robot-KUKA-KR-6-37-2048.jpg)
![Din´amica de Robots
Caracter´ısticas del Robot
Cinem´atica
Simulaciones
Bibliograf´ıa
Descripci´on de la trayectoria
Gr´aficas de articulaci´on
Modelaci´on en Matlab c
Gr´aficas de articulaci´on - Velocidad
0 100 200 300 400 500 600 700 800 900 1000
−4
−2
0
2
4
6
8
10
θ[rad/s]
Gráfica de velocidad angular para q1
.
θ[rad/s]
.
Muestra Muestra
Muestra
0 100 200 300 400 500 600 700 800 900 1000
−12
−10
−8
−6
−4
−2
0
2
4
6
Gráfica de velocidad angular para q2
0 100 200 300 400 500 600 700 800 900 1000
−0.3
−0.2
−0.1
0
0.1
0.2
0.3
0.4
Gráfica de velocidad angular para q3
0 100 200 300 400 500 600 700 800 900 1000
−1.5
−1
−0.5
0
0.5
1
1.5
2
Gráfica de velocidad angular para q4
0 100 200 300 400 500 600 700 800 900 1000
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
Gráfica de velocidad angular para q5
0 100 200 300 400 500 600 700 800 900 1000
−3
−2
−1
0
1
2
3
Gráfica de velocidad angular para q6
Universidad NACIONAL de Colombia. Din´amica de Robots - KUKA KR 6-2](https://image.slidesharecdn.com/dinamicaderobots-sierrasierranelsonariel-kuka-kr6-2-130924231741-phpapp01/75/Estudio-de-Robot-KUKA-KR-6-38-2048.jpg)