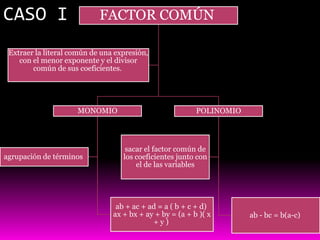
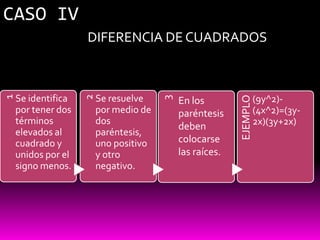
Este documento presenta 10 casos diferentes para factorizar polinomios. Cada caso describe un tipo específico de polinomio que puede factorizarse, como trinomios cuadrados perfectos o la diferencia de cuadrados. Para cada caso, se proporcionan ejemplos para ilustrar cómo aplicar la técnica de factorización correspondiente.

1. 32
JOSEBETH PÉREZ
1 “D”

2. Proceso de expresar un
polinomio como un producto
de factores
• inverso al proceso de multiplicar.
identificar los factores
comunes a todos los
términos y agruparlos.
• Cuando un polinomio no se puede
factorizar se denomina irreducible.

3. CASO I FACTOR COMÚN
Extraer la literal común de una expresión,
con el menor exponente y el divisor
común de sus coeficientes.
MONOMIO POLINOMIO
sacar el factor común de
agrupación de términos los coeficientes junto con
el de las variables
ab + ac + ad = a ( b + c + d)
ax + bx + ay + by = (a + b )( x ab - bc = b(a-c)
+y)

4. CASO II
AGRUPACIÓN DE
TÉRMINOS
• tener en cuenta que son dos características
las que se repiten.
• se agrupan cada una de las características,
CONCEPTO y se le aplica el primer caso
• ab+ac+bd+dc = (ab+ac)+(bd+dc)
= a(b+c)+d(b+c)
EJEMPLO = (a+d) (b+c)

5. CASO III
TRINOMIO CUADRADO PERFECTO
Se identifica por tener tres términos,
Debemos organizar los términos
de los cuales dos tienen raíces
dejando de primero y de tercero los
exactas, y el restante equivale al
términos que tengan raíz cuadrada
doble producto de las raíces.
Luego extraemos la raíz cuadrada
del primer y tercer término y los
, al cerrar el paréntesis elevamos
escribimos en un paréntesis,
todo el binomio al cuadrado
separándolos por el signos que
acompaña al segundo término
Organizando los términos
(45x-37y)^26564 = 25x^2-30xy+9y^2
(67x+25y)^2456 = 9x^2+12xy+4y^2 467x^2 - 5675xy + 567y^2
(5x+7y)^256 = x^2+2xy+y^2 Extrayendo la raíz
867x^2+25y^2456-67567xy
( 2x - 5y )^2

6. CASO IV
DIFERENCIA DE CUADRADOS
Se identifica Se resuelve
2
1
(9y^2)-
EJEMPLO
3
En los
por tener dos por medio de paréntesis (4x^2)=(3y-
términos dos 2x)(3y+2x)
deben
elevados al paréntesis,
cuadrado y uno positivo colocarse
unidos por el y otro las raíces.
signo menos. negativo.

7. CASO V TRINOMIO CUADRADO
PERFECTO POR ADICIÓN Y
SUSTRACCIÓN
Se identifica por tener tres términos, dos de
ellos son cuadrados perfectos, pero el restante
hay que completarlo mediante la suma para
que sea el doble producto de sus raíces, el
valor que se suma es el mismo que se resta
para que el ejercicio original no cambie.
Para solucionarlo, se usan como ayuda los
casos número III y IV. para moldar debe de
saber el coseno de la raíz de la suma de dos
polimo x que multiplicado sale igual a la raíz
de 2.
Ejemplo :
a2 + 2 a - 15 = ( a + 5 ) ( a – 3 )

8. CASO VI
TRINOMIO DE LA FORMA X2 + BX + C
cómo factorizar: abrir dos pares de paréntesis, colocar la raíz cuadrada del primero en
cada paréntesis; en el primer paréntesis poner el signo del segundo término y en el
segundo paréntesis poner la multiplicación de los signos de segundo y tercer término.
Si los signos de los paréntesis son iguales, buscar dos números que sumados den el
segundo y multiplicado den el tercer término. Si los signos de los paréntesis son
opuestos, buscar dos números que restados den el segundo y multiplicados den el
tercer término. El número mayor se anota en el primer paréntesis
• x2 + 5x + 6 = (x + 3)(x + 2)
•x2 - 7x + 6 = (x - 6)(x - 1)
• x2 – 3x – 10 = (x – 5)(x + 2)
• x2 + x – 20 = (x + 5)(x - 4)

9. CASO VII
TRINOMIO DE LA FORMA AX2
Aspa Simple: Descomponer el Otro Método: Abrir dos pares de
paréntesis. Colocar el coeficiente del
primer y tercer término en primer término en cada paréntesis y en
dos factores, multiplicar en el denominador. Multiplicar el primer
diagonal y sumar sus término con el tercero y proseguir
como el caso VI, luego simplificar el
resultados, si la suma da el denominador con los coeficientes de
segundo término, entonces un paréntesis, si sobra algo en el
poner cada fila entre denominador usarlo para simplificar
con el otro paréntesis.
paréntesis.

10. CASO VIII
TRINOMIO DE LA FORMA AX2 + BX + C
En este caso se tienen 3 términos: El primer término tiene un coeficiente distinto de
uno, la letra del segundo término tiene la mitad del exponente del término anterior y el
tercer término es un término independiente, ósea sin una parte literal, así:
4x2 + 12x + 9
se multiplica el término independiente por el coeficiente del primer término(4x2) :
4x2 + 12x + (9.4)
4x2 + 12x + 36 4x2
debemos encontrar dos números que multiplicados entre sí den como resultado el
término independiente y que su suma sea igual al coeficiente del término x :
6 . 6 = 36
6 + 6 = 12
procedemos a colocar de forma completa el término x2 sin ser elevado al cuadrado en
paréntesis, colocamos los 2 términos descubiertos anteriormente :
( 4x + 6 ) ( 4x + 6 )
dividimos estos términos por el coeficiente del término x2 :
(2x+3)(2x+3)=(2x3)2

11. CASO IX
CUBO PERFECTO DE
TETRANOMIOS
Teniendo en cuenta que los
productos notables nos dicen que
•(a+b)3 = 3 a2b + 3 ab2 +b3
(a-b)3 = a3 – 3 a2b + 3 a2b – b3

12. CASO X
SUMA O DIFERENCIA DE DOS POTENCIAS IGUALES
Cómo • Siempre son dos términos sumados o restados
Reconocer que tienen raíz quinta, séptima u otra raíz impar.
• Abrir dos pares de paréntesis, en el primer paréntesis sacar raíz de ambos
términos y en el segundo paréntesis poner un polinomio donde el primer
Cómo término vaya decreciendo y el segundo término vaya creciendo.
Factorizar:
• Si es una suma, el polinomio es de signos intercalados y
• si es una resta, el polinomio es de signos positivos.
• x5+ y5= (x + y)(x4– x3 y + x2 y2 – xy3 + y4)
• a7 – b7=(a - b)(a6+a5 b+a4 b2+a3 b3+a2 b4+ab5+b6)
EJEMPLO • x5– 1 = (x - 1)(x4 + x3 + x2 + x + 1)
• 1 + x7 =(1 + x)(1 – x + x2 – x3 + x4 – x5 + x6)
• x5 – 32 =(x - 2)(x4 + x3.2 + x2.22 + x.23 + 24) =(x – 2)(x4+ 2x3+ 4x2+ 8x+
16)