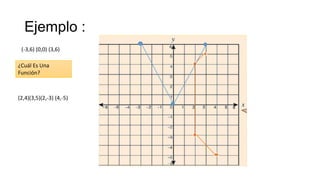
Este documento explica conceptos básicos sobre funciones. Define una función como una relación entre un conjunto de entrada (dominio) y un conjunto de salida (codominio) de forma que a cada elemento de entrada le corresponde un único elemento de salida. Explica que las funciones se pueden representar mediante diagramas, tablas de valores, gráficas y pares ordenados, y que para que una relación sea una función, cada elemento de entrada debe corresponder a un único elemento de salida.

1. Centro bachillerato tecnológico agropecuario
#287
materia: calculo
Facilitadora : Berna Yurian Rojo
Equipo: Daira vergara
J. Alberto Pineda
Jannely Gonzales
Moisés
Jorge Cuadra
Semestre: IV Grupo : A
Paso de Arena Gro.17 de Febrero
del 2014

3. ¿Qué es una función?
• Una función es como una máquina: tiene una entrada y
una salida.
• Y lo que sale está relacionado de alguna manera con lo que
entra.
• En matemática, una función es una relación entre un
conjunto dado X (llamado dominio) y otro conjunto de
elementos Y(llamado (codominio) de forma que a cada
elemento x del dominio le corresponde un único
elemento f(x) del codominio (los que forman
el recorrido, también llamado rango o ámbito).

4. Nombres
Primero, es útil darle un nombre a una función. El nombre más común es "f", pero
puedes ponerle otros como "g" .
Y también está bien darle nombre a lo que se va adentro de la función, se pone
entre paréntesis () después del nombre de la función:
Así que f(x) te dice que la función se llama "f", y "x" se pone dentro
Y normalmente verás lo que la función hace a la entrada:
f(x) = x2 nos dice que la función "f" toma "x" y lo eleva al cuadrado.
Así que con la función "f(x) = x2", una entrada de 4 da una salida de 16. De hecho
podemos escribir f(4) = 16.
Nota: a veces las funciones no tienen nombre, y puede que veas algo como y = x2

6. Representación de las funciones
Diagrama
Tabla de valores
Grafica
Pares ordenados
Plano cartesiano

7. Forma de diagrama digital o sagital
• en este tipo de grafica se reconoce como función si a un conjunto del
elemento inicial le corresponde un único elemento del conjunto final
a esto le corresponde una función.
• Tiene que tener un dominio y rango
• Tener pares ordenados.

8. La condición para que una relación entre conjuntos sea función es que cada elemento de primer
conjunto salga solo una flecha

11. Sacar el dominio y
el rango

12. Grafica
Para saber que una grafica es una función
Es que para cada X corresponde una única
Y.
Cuando la línea de la grafica es vertical no
se considera función. Porque toca 2
puntos.

13. ¿Cuáles se consideran función y cual no ?

14. Pares ordenados
En matemáticas, un par ordenado es una pareja de objetos
matemáticos, en la que se distingue un primer elemento y
un segundo elemento. El par ordenado cuyo primer elemento
es a y cuyo segundo elemento es b se denota como (a, b).

15. Pares ordenados
Ejemplos de ocho puntos localizados en el plano
cartesiano mediante pares ordenados

16. • Para saber si es una función se debe tener en cuenta que el primer
termino no se puede repetir a penos de que su signo de negativo o
positivo sean diferentes .
Como saber si en una función

17. Ejemplo :
(-3,6) (0,0) (3,6)
¿Cuál Es Una
Función?
(2,4)(3,5)(2,-3) (4,-5)

18. Representación en tablas
¿Como saber si corresponde a una función?
La y siempre va a depender de la x , y. y no se puede repetir el
primer termino x

20. Ejercicios
• H(X)=x³-2x²-x+2 : resolverla en 0,1,2,3 , Colocarlo en una tabla , sacar
los pares ordenados y graficarlos en el plano
• Y=5x-3 : resolverlas en -3,0,2 y colocarlo en una tabla
• Y= X² : resolverlas en -3, 0, 3 dibujar grafica y colocarlo en una tabla

21. Conclusión
• una función relaciona entradas con salidas
• una función toma elementos de un conjunto (el dominio) y los
relaciona con elementos de un conjunto (el codominio).
• las salidas (los verdaderos valores de la función) se llaman
la imagen o rango
• una entrada sólo produce una salida (no una u otra)
• una entrada y la salida que corresponde se llaman juntos un par
ordenado
• así que una función también se puede ver como un conjunto de pares
ordenado