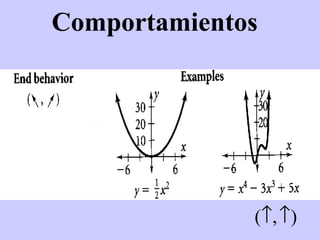
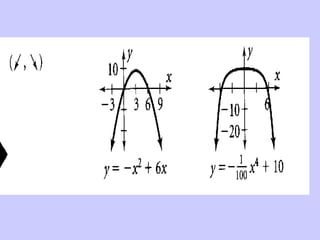
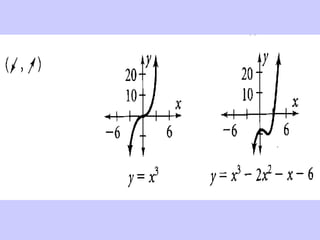
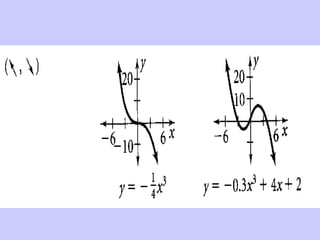
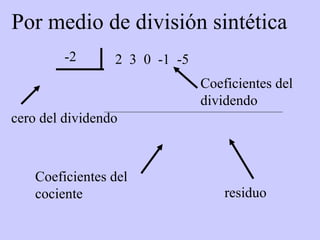
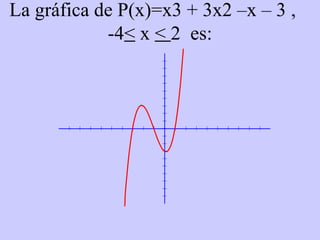
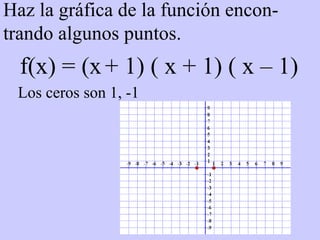
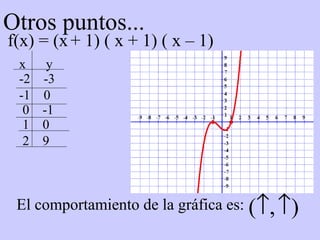
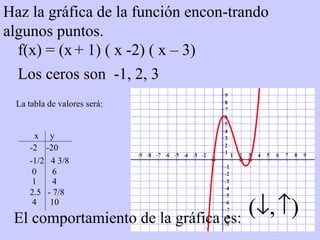
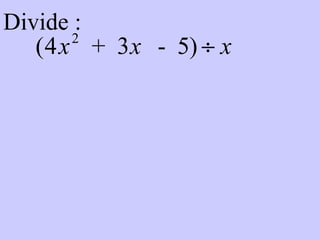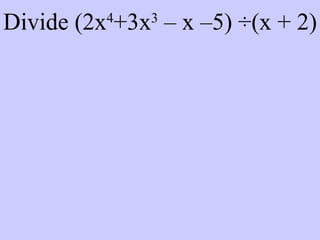Este documento resume conceptos básicos sobre funciones polinómicas. Explica que una función polinómica es aquella donde hay varios términos con grados sumados o restados y una constante. También proporciona ejemplos de cómo escribir funciones polinómicas en forma estándar e identificar sus coeficientes. Finalmente, asigna ejercicios de práctica relacionados con funciones polinómicas.

1. Funciones Polinómicas Profa. Carmen Batiz UGHS

2. REPASEMOS...

3. Función Lineal f(x) = mx + b f(x) = b

4. Función Cuadrática f(x) = ax 2 + bx + c

5. Función Polinómica de grado n en x: F(x) = a n x n + a n –1 x n-1 + a n – 2 x n –2 + ...+ a 1 x + a 0 Donde n es un entero no-negativo y a n , a n-1 ,a n-2 , , ...,a 1 , a 0 Son números reales con a n  0 Los números a n , a n-1 ,a n-2 , , ...,a 1 , a 0 son coeficientes del polinomio.

6. Las funciones polinómicas... Son aquellas donde hay varios términos con sus grados sumados o restados y una constante. Deben escribirse en forma descen-dente por el grado de la variable, esto es en “forma standard”

7. Ejemplo: Si f(x) = 2x 3 –5x 2 + 3 Los coeficientes de la función son: 2, -5, 0, 3 Entonces a 3 = 2, a 2 = -5, a 1 = 0 y a 0 = 3 Es un polinomio de grado 3 y es un trinomio.

8. Otros ejemplos: Escribe en forma standard, indica los coeficientes de la función, y clasifícalo por el número de término y el grado. f(x) = 3x – 6x 2 + 5 y = 3x 3 + x 2 –4x + 2x 3

9. f(x) = 3x – 6x 2 + 5 y = 3x 3 + x 2 –4x + 2x 3 Contestaciones: f(x) = – 6x 2 +3x + 5; -6, 3, 5 2. y = 5x 3 + x 2 – 4x ; 5, 1, 0 -4

10. Asignación: 265 ( 1-9) 6-2 Example Exercises 1-24 Mixed Exercises 2 - 46

11. Comportamientos

15. Señala por el tipo de compotamiento que tiene cada función f(x) = x 3 –3x 2 + x - 2. Estima el intercepto de x y de y. x -10 -3 -2 -1 0 1 2 3 4 10 y -1312 -59 -24 -7 -2 -3 -4 1 18 708

16. Señala por el tipo de compotamiento que tiene cada función f(x) = x 3 –3x 2 + x - 2. Estima el intercepto de x y de y. x -10 -3 -2 -1 0 1 2 3 4 10 y -1312 -59 -24 -7 -2 -3 -4 1 18 708 El intercepto de y es –2. Como los valores de x y y van de lo negativo a lo positivo su compor-tamiento es El intercepto de x esta entre 2 y 3.

17. Asignación 6-2 p. 19 Example Ex. 1-24 p.20 Mixed Ex 2-46

18. División de Polinomios

19. Divide : 5 435 8 -40 3 5 7 -35 0 Verificación: 87 x 5 + residuo

20. Divide :

21. Divide : x 4x -4x 2 - 5 0x 2 + 3 - 3x 0x Verificación: x (4x+3) + -5 + 3x R = -5 4x 2 +3x -5

22. Intenta: -2x -6x 2 0x 2 + 1 3x - 3x + 9 R = 9 -3x (-2x + 1) + 9 Verificación: 6x 2 – 3x + 9 0x + 9

23. Divide : 3x 2 -3x 3 + 9x 2 -1 0x 2 +8x 2 + 8x - 8x 2 + 24x 0x+ 26x Verificación: ( x - 3) (3x 3 +8x +26) + 77 + 2x R = 77 + 26 - 26x + 78 77

24. Intenta:

25. Intenta: 2x 2 -2x 4 + 2x 3 – 2x 2 0x 4 - x 3 + 3x 2 – x x 3 – x 2 + x + 2x 0x 3 + 2 x 2 + 3x + 7 + 2 – 2x 2 + 2x - 2 5x + 5

26. Verificación (2x 2 - x + 2) ( x 2 – x + 1) + (5x + 5) 2x 4 - 2x 3 + 2x 2 - x 3 + x 2 - x 2x 2 - 2x + 2 5x + 5 2x 4 - 3x 3 + 5x 2 + 2x + 7

27. Generalización: Dividendo = Cociente x divisor + residuo -2x + 1 dividendo cociente divisor R = 9

28. Generalización: Dividendo = Cociente x divisor + residuo (2x 2 - x + 2) ( x 2 – x + 1) + (5x + 5)

29. Intenta:

30. Intenta:

31. Ejercicios de Práctica 6-5 p. 25 Example Exercises (1-10) p. 26 Mixed Exercises (13-24)

32. División Sintética

33. Divide (2x 4 +3x 3 – x –5) ÷(x + 2)

34. Divide (2x 4 +3x 3 – x –5) ÷(x + 2) 2x 3 -2x 4 - 4x 3 0x 4 - x 3 + 0x 2 - x 2 x 3 + 2x 2 0x 2 + 2x 2 - x + 2x - 2x 2 – 4x 0x 2 – 5x – 5 – 5 5x + 10 0x + 5 R=5

35. Verificación: (2x 3 – x 2 + 2x – 5) (x + 2 ) + 5 2x 4 – x 3 + 2x 2 – 5x + 4x 3 - 2x 2 + 4x - 10 + 5 2x 4 + 3x 3 + 0x 2 – x - 5 Y...

36. Por medio de división sintética Coeficientes del dividendo cero del dividendo 2 3 0 -1 -5 -2 residuo Coeficientes del cociente

37. Por medio de división sintética 2 3 0 -1 -5 -2 -4 2 -1 2 2 -4 -5 10 -5 El cociente es: 2x 3 –x 2 +2x -5

38. Intentemos... -13x + x 3 + 12 ÷ x + 4

39. Intentemos... -13x + x 3 + 12 ÷ x + 4 1 0 -13 12 - 4 1 -4 -4 16 3 -12 0 El cociente es: x 2 – 4x + 3

40. Intenta: Divide cada una de los ejercicios utilizando la división sintética. (4x 5 –30x 3 – 50x –2) ÷( x + 3) (5 + 4x 3 – 3x) ÷(2x – 3) Contestaciones: 4x 4 –12x 3 + 6x 2 –18x +4 R = -14 2x 2 + 3x + 3 R =14

41. Ejercicios: 6.5 Example Exercises 11-18 Mixed Exercises 1-12

42. Teorema del Residuo y del Factor

43. Si se divide 2x 4 – 5x 3 – 4x 2 + 13 entre x – 3 el cociente es: 2x³ + x² – x – 3 + 4 donde x = 3 x - 3 Si R es el residuo después de dividir el polinomio P(x) entre x – r entonces P(r) = R

44. P(x)= 2x 4 – 5x 3 – 4x 2 + 13 entonces P(3) = 4 2(3)4 – 5(3)3 – 4(3)2 + 13 = 4 2(81) – 5(27) – 4(9) + 13 = 4 ? 162 – 135 – 36 + 13 = 4 162 – 135 – 36 + 13 = 4 4 = 4

45. Si P(x) = 4x 4 + 10x 3 + 19x + 5, encuentra P(-3) usando el teorema del residuo y la división sintética y evaluando P(-3) directamente. 4 10 0 19 5 -3

46. Si P(x) = 4x 4 + 10x 3 + 19x + 5, encuentra P(-3) usando el teorema del residuo y la división sintética y evaluando P(-3) directamente. 4 10 0 19 5 -3 4 -12 -2 6 6 -18 1 -3 2

47. Si P(x) = 4x 4 + 10x 3 + 19x + 5, entonces P(-3) Si P(-3) =

48. Si P(x) = 4x 4 + 10x 3 + 19x + 5, entonces P(-3) Si P(-3) = 4(-3)4 + 10(-3)3 + 19(-3) + 5 = 4(81)4 +10(-27)3 +19(-3)+ 5 = 324 + -270 + -57 + 5 P(-3) = 2

49. Haz la gráfica de P(x) = x 3 + 3x 2 –x – 3, -4 < x < 2 1 3 -1 -3 -4 -3 -2 -1 0 1 2

50. Haz la gráfica de P(x) = x 3 + 3x 2 –x – 3 , -4 < x < 2 1 3 -1 -3 -4 1 -1 3 -15 = P (-4) -3 1 0 -1 0 = P (-3) -2 1 1 -3 3 = P(-2) -1 1 2 -3 0 = P(-1) 0 1 3 -1 -3 = P(0) 1 1 4 3 0 = P(1) 2 1 5 9 -15 = P(2)

51. La gráfica de P(x)=x3 + 3x2 –x – 3 , -4 < x < 2 es:

52. Teorema del factor Si r es un cero del polinomio P(x) , entonces x – r es un factor de P(x) ; inversamente si x – r es un factor de P(x) , entonces r es un cero de P(x).

53. Haz la gráfica de P(x) = x 3 + 3x 2 –x – 3 , -4 < x < 2 1 3 -1 -3 -4 1 -1 3 -15 = P (-4) -3 1 0 -1 0 = P (-3) -2 1 1 -3 3 = P(-2) -1 1 2 -3 0 = P(-1) 0 1 3 -1 -3 = P(0) 1 1 4 3 0 = P(1) 2 1 5 9 -15 = P(2)

54. Utiliza el teorema del factor para probar que x +1 es un factor de P(x) = x 25 + 1

55. Utiliza el teorema del factor para probar que x +1 es un factor de P(x) = x 25 + 1 x + 1 = x – (-1) Entonces r = -1 P(-1) = -1 25 + 1 P(-1) = -1 + 1 P(-1) = 0 Entonces –1 es un cero de la función

56. Indica cuáles son los ceros de P(x) = 3(x-5) (x+2) (x-3)

57. Indica cuáles son los ceros de P(x) = 3(x-5) (x+2) (x-3) Los ceros de la función es cuando P(x) = 0... Entonces: 0 = 3( x – 5)(x+2) (x- 3) Entonces los ceros son : 5, –2 y 3

58. Utiliza el teorema del factor para probar que x -1 es un factor de P(x) = x 54 - 1 INTENTA

59. Utiliza el teorema del factor para probar que x -1 es un factor de P(x) = x 54 - 1 P(1) = 1 54 - 1 P(1) = 1 - 1 P(1) = 0 Entonces 1 es un cero de la función INTENTA

60. Indica cuáles son los ceros de P(x) = 2(x+3) (x+7) (x-8)(x + 1) INTENTA

61. Indica cuáles son los ceros de P(x) = 2(x+3) (x+7) (x-8)(x + 1) Los ceros de la función es cuando P(x) = 0... Entonces: Entonces los ceros son : -3,–7, 8 y -1 INTENTA

62. Ejercicios de Práctica Ejercicios 3.3 BARNETT : 7-30 35-38 impares (para entregar) Ejercicios 6.3 Example Exercises: 2-10 13-33 Ejercicios 6.3 Mixed Exercises: 1-47

63. Haciendo gráficas polinómicas

64. Ceros de una función: Def. Son las soluciones o raíces de una función. f(x) = 0

65. Función Lineal f(x) = x - 2

66. Función Lineal f(x) = x - 2 x – 2 = 0 x = 2 El cero o intercepto en x de ésta función es 2

67. Función cuadrática f(x) = x 2 – 4x - 5

68. Función cuadrática f(x) = x 2 – 4x - 5 El cero o intercepto en x de ésta función es 5 y -1 x 2 – 4x - 5 = 0 (x – 5) ( x + 1) = 0 x = 5 ó x = -1

69. Función cúbica f(x) = x 3 + x 2 – x - 1

70. Función cúbica f(x) = x 3 + x 2 – x - 1 El cero o intercepto en x de ésta función es 1 y -1 (x + 1) ( x + 1) ( x – 1) = 0 x = 1 ó x = -1 x 2 ( x + 1) – 1(x + 1) = 0 (x + 1) ( x 2 -1) = 0 Cuando hay dos factores iguales se dice que hay ceros de multiplicidad

71. Haz la gráfica de la función encon-trando algunos puntos. f(x) = (x + 1) ( x + 1) ( x – 1) Los ceros son 1, -1

72. Otros puntos... x y -2 -3 -1 0 0 -1 1 0 2 9 f(x) = (x + 1) ( x + 1) ( x – 1) El comportamiento de la gráfica es:

73. Haz la gráfica de la función encontrando algunos puntos. f(x) = (x + 1) ( x -2) ( x – 3)

74. Haz la gráfica de la función encon-trando algunos puntos. f(x) = (x + 1) ( x -2) ( x – 3) Los ceros son -1, 2, 3 La tabla de valores será: x y -2 -20 -1/2 4 3/8 0 6 1 4 2.5 - 7/8 4 10 El comportamiento de la gráfica es:

75. Ejercicios de Práctica

78. Asignación: p.21 Practice 6.3 Example Exercises p.22 Mixed Exercises