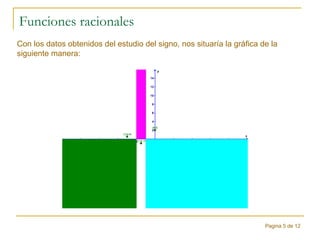
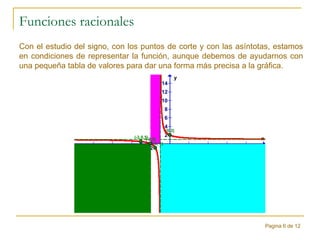
Este documento explica las funciones racionales a través del estudio de la función f(x)=(x+2)/(x+1). Explica cómo calcular el dominio, los puntos de corte con los ejes, las asíntotas verticales y horizontales, y el signo de la función para representarla gráficamente. Muestra cómo la función es positiva para x<-2 y x>-1, y negativa para -2<x<-1. Finalmente, ilustra la representación gráfica de varias funciones racionales.

1. Funciones Racionales Segundo ciclo de ESO

2. Funciones racionales Se conocen con el nombre de funciones racionales aquellas funciones cuya expresión es una fracción algebraica: Un ejemplo de función racional: Vamos a realizar un estudio sencillo de la función que nos permita obtener su representación gráfica: Dominio de definición de la función : D(f)=  – {–1 } Puntos de corte con los ejes : Con el eje X : y = 0 x + 2 = 0 x =– 2 ( – 2,0) Con el eje Y : x = 0 (0,2) Pagina 2 de 12

3. Funciones racionales Asíntotas : Verticales : Para calcularlas igualamos el denominador a cero: x + 1 = 0 x =– 1 Horizontales : Dividimos los coeficientes de la potencia mayor de x : y = 1 Signo de la función: Para el conocimiento de la función a efectos de dibujar su gráfica, es muy importante el estudio del signo de la función. Tenemos que obtener los puntos donde la función cambia de signo: Numerador: x + 2 = 0 x =– 2 Denominador: x +1 = 0 x =–1 Pagina 3 de 12

4. Funciones racionales Damos valores menores que – 2 , entre – 2 y – 1 y mayores que – 1 , para observar como cambia el signo de la función: Para x =– 3 la función es positiva en el intervalo (–  , –2) , podemos tachar la parte negativa dado que ahí no hay función. (Rayado verde de la figura) Para x =– 1,5 la función es negativa en el intervalo (–2, –1) , podemos tachar la parte positiva dado que ahí no hay función. (Rayado fucsia de la figura) Para x =0 la función es positiva en el intervalo (–1,  ) , podemos tachar la parte negativa dado que ahí no hay función. (Rayado azul de la figura) Pagina 4 de 12

5. Funciones racionales Con los datos obtenidos del estudio del signo, nos situaría la gráfica de la siguiente manera: Pagina 5 de 12

6. Funciones racionales Con el estudio del signo, con los puntos de corte y con las asíntotas, estamos en condiciones de representar la función, aunque debemos de ayudarnos con una pequeña tabla de valores para dar una forma más precisa a la gráfica. Pagina 6 de 12

7. Funciones racionales Veamos a continuación la representación gráfica de algunas funciones racionales: Pagina 7 de 12

8. Funciones racionales Pagina 8 de 12

9. Funciones racionales Pagina 9 de 12

10. Funciones racionales Pagina 10 de 12

11. Funciones racionales Pagina 11 de 12

12. Funciones racionales Pagina 12 de 12