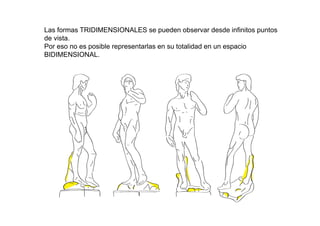
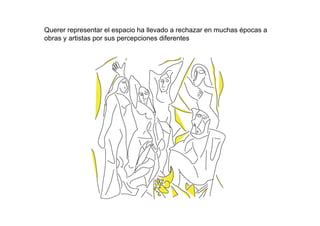
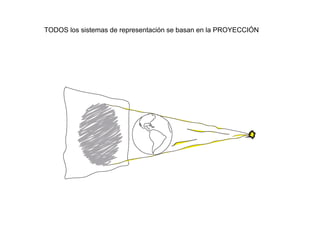
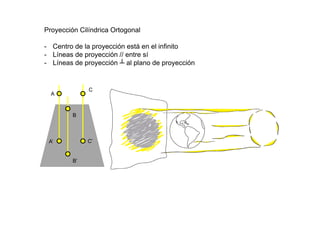
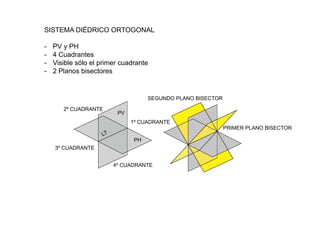
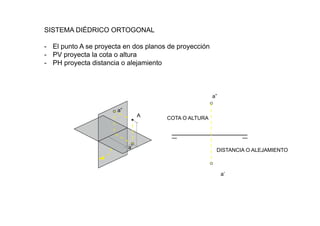
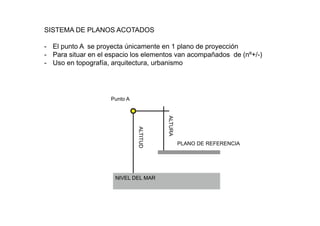
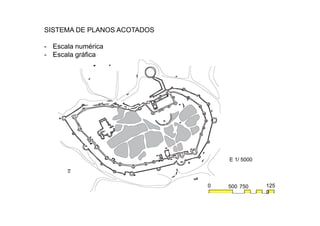
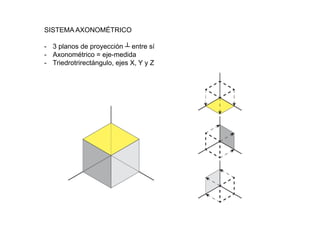
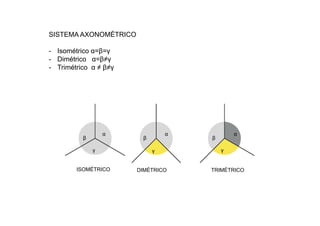
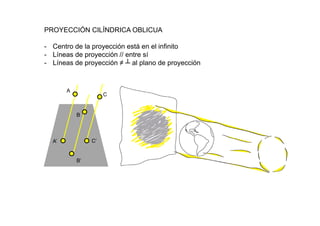
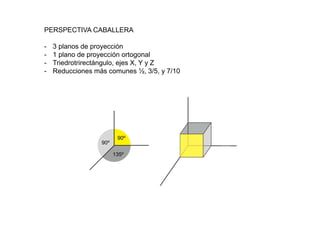
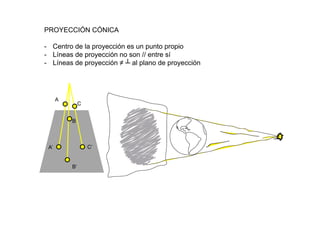
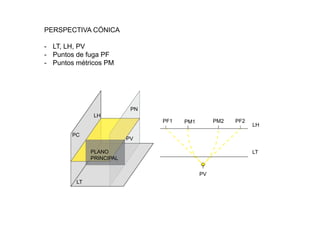
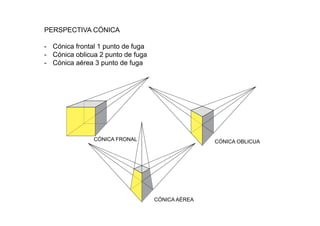
Este documento describe los fundamentos y finalidades de la geometría descriptiva. Explica que debido a que las formas tridimensionales se pueden observar desde múltiples puntos de vista, no es posible representarlas completamente en un espacio bidimensional. Luego, detalla varios sistemas de proyección geométrica como la proyección cilíndrica ortogonal, el sistema diédrico ortogonal, el sistema de planos acotados y el sistema axonométrico, que permiten representar objetos tridimensionales en el plano. Finalmente

1. FUNDAMENTOS Y FINALIDADES DE LA
GEOMETRÍA DESCRIPTIVA
JESÚS JAREÑO ESCUDERO

2. Las formas TRIDIMENSIONALES se pueden observar desde infinitos puntos
de vista.
Por eso no es posible representarlas en su totalidad en un espacio
BIDIMENSIONAL.

3. Dibujar nos sirve para que otros puedan ver, fabricar, aprender…

4. La GEOMETRÍA DESCRIPTIVA tuvo su origen en Caldea y Egipto

5. La GEOMETRÍA DESCRIPTIVA tuvo su origen en Caldea y Egipto

6. La GEOMETRÍA DESCRIPTIVA tuvo su origen en Caldea y Egipto

7. La GEOMETRÍA DESCRIPTIVA tuvo su origen en Caldea y Egipto

8. El arte egipcio evita toda relación con el espacio

9. El Renacimiento evoluciona la representación del espacio pictórico
bidimensional a uno tridimensional gracias a la perspectiva

10. Querer representar el espacio ha llevado a rechazar en muchas épocas a
obras y artistas por sus percepciones diferentes

11. TODOS los sistemas de representación se basan en la PROYECCIÓN

12. Proyección Cilíndrica Ortogonal
- Centro de la proyección está en el infinito
- Líneas de proyección // entre sí
- Líneas de proyección ┴ al plano de proyección
A
A’
B’
C’
B
C

13. SISTEMA DIÉDRICO ORTOGONAL
- PV y PH
- 4 Cuadrantes
- Visible sólo el primer cuadrante
- 2 Planos bisectores
1º CUADRANTE
4º CUADRANTE
2º CUADRANTE
3º CUADRANTE
PV
PH
PRIMER PLANO BISECTOR
SEGUNDO PLANO BISECTOR

14. SISTEMA DIÉDRICO ORTOGONAL
- El punto A se proyecta en dos planos de proyección
- PV proyecta la cota o altura
- PH proyecta distancia o alejamiento
COTA O ALTURA
DISTANCIA O ALEJAMIENTO
a”
a’
a”
a’
A

15. SISTEMA DE PLANOS ACOTADOS
- El punto A se proyecta únicamente en 1 plano de proyección
- Para situar en el espacio los elementos van acompañados de (nº+/-)
- Uso en topografía, arquitectura, urbanismo
Punto A
ALTURA
ALTITUD
PLANO DE REFERENCIA
NIVEL DEL MAR

16. SISTEMA DE PLANOS ACOTADOS
- Escala numérica
- Escala gráfica
E 1/ 5000
0 500 750 125
0

17. SISTEMA AXONOMÉTRICO
- 3 planos de proyección ┴ entre sí
- Axonométrico = eje-medida
- Triedrotrirectángulo, ejes X, Y y Z

18. α
SISTEMA AXONOMÉTRICO
- Isométrico α=β=ү
- Dimétrico α=β≠ү
- Trimétrico α ≠ β≠ү
α α
β β β
ү ү ү
ISOMÉTRICO DIMÉTRICO TRIMÉTRICO

19. PROYECCIÓN CILÍNDRICA OBLICUA
- Centro de la proyección está en el infinito
- Líneas de proyección // entre sí
- Líneas de proyección ≠ ┴ al plano de proyección
A
A’
B’
C’
B
C

20. PERSPECTIVA CABALLERA
- 3 planos de proyección
- 1 plano de proyección ortogonal
- Triedrotrirectángulo, ejes X, Y y Z
- Reducciones más comunes ½, 3/5, y 7/10
90º
135º
90º

21. PROYECCIÓN CÓNICA
- Centro de la proyección es un punto propio
- Líneas de proyección no son // entre sí
- Líneas de proyección ≠ ┴ al plano de proyección
A
A’
B’
C’
B
C

22. PERSPECTIVA CÓNICA
- LT, LH, PV
- Puntos de fuga PF
- Puntos métricos PM
PV
LH
LT
PLANO
PRINCIPAL
PC
PN
LT
LH
PV
PF1 PF2PM1 PM2

23. PERSPECTIVA CÓNICA
- Cónica frontal 1 punto de fuga
- Cónica oblicua 2 punto de fuga
- Cónica aérea 3 punto de fuga
CÓNICA FRONAL CÓNICA OBLICUA
CÓNICA AÉREA