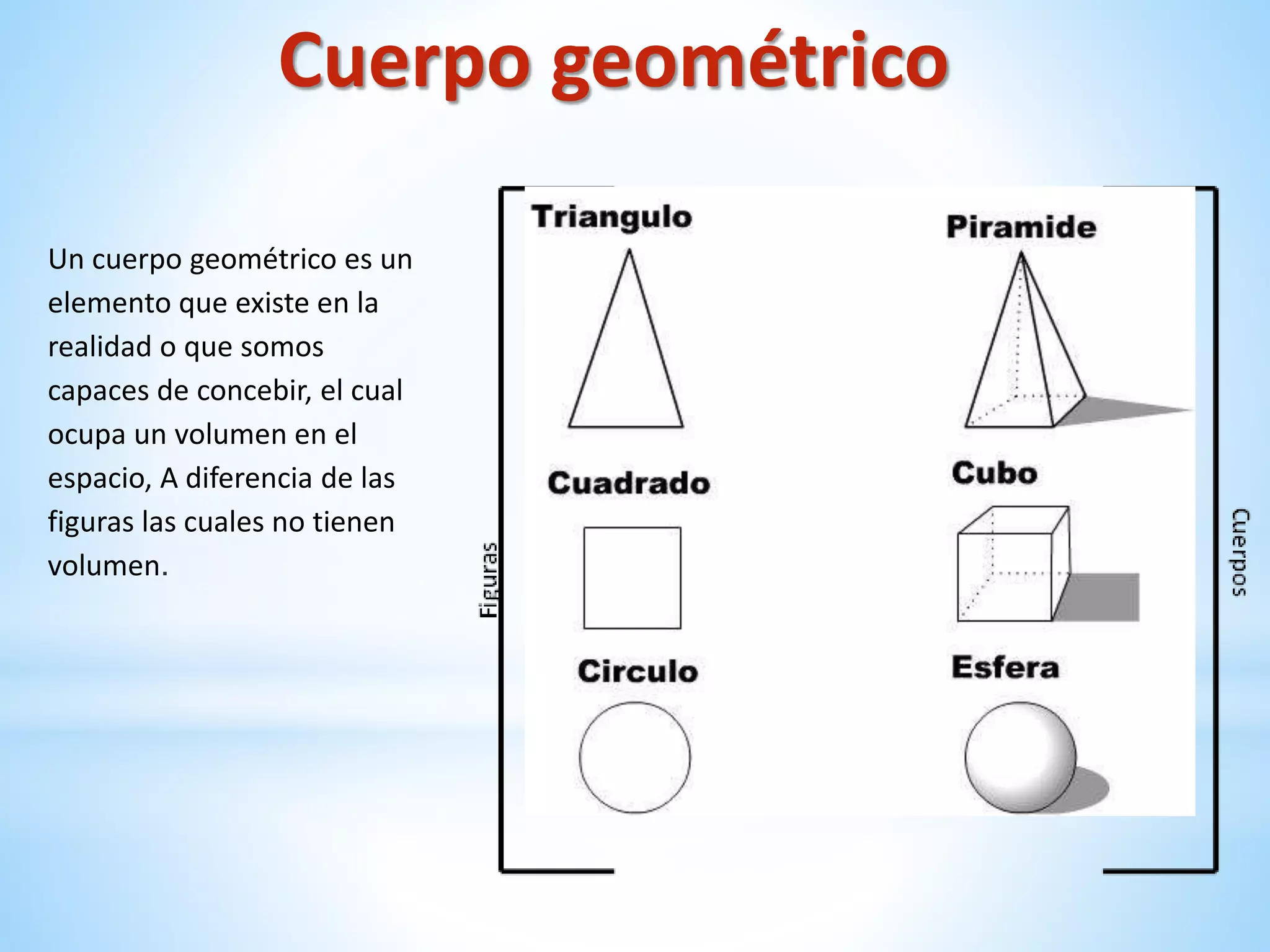
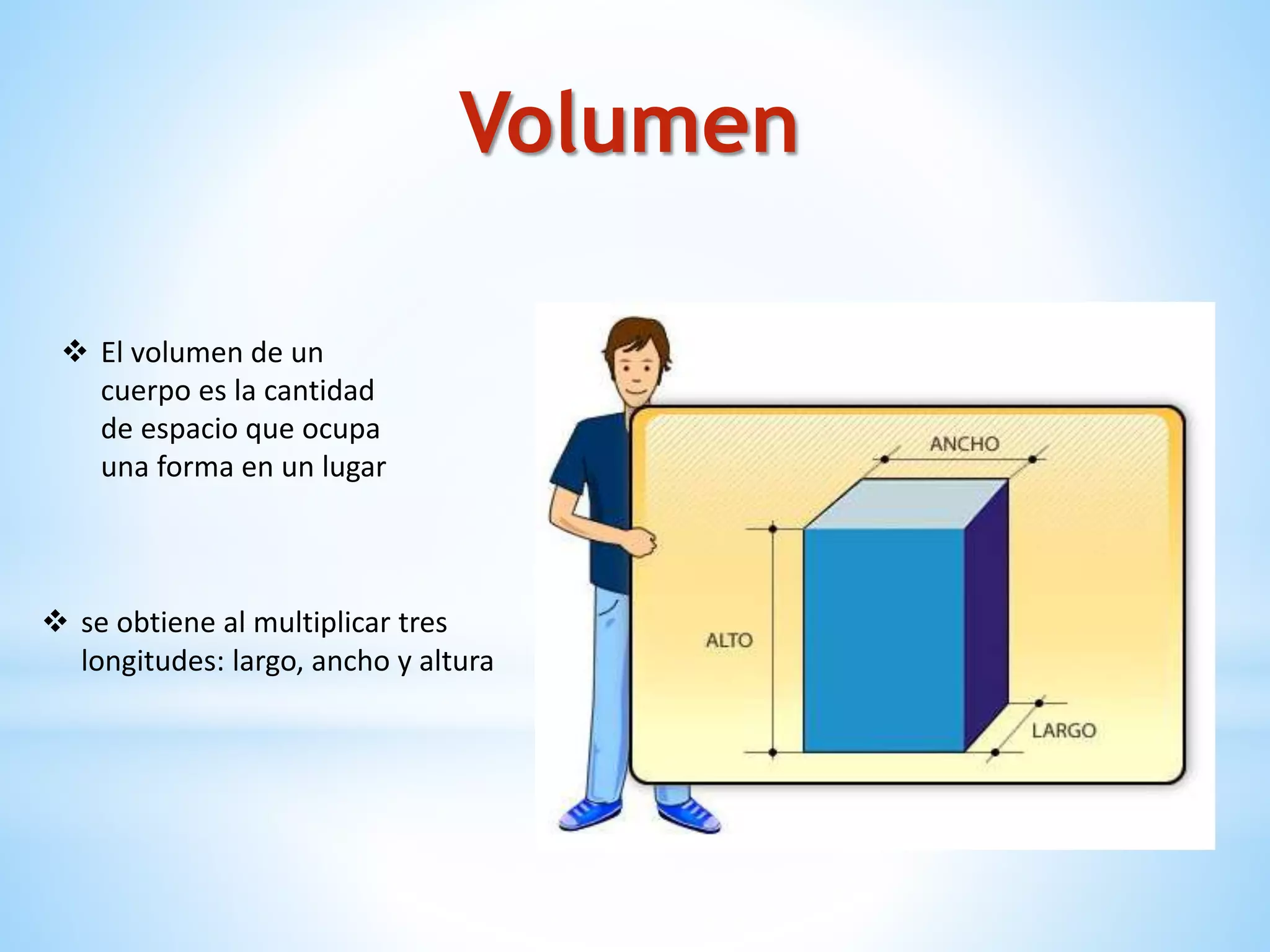
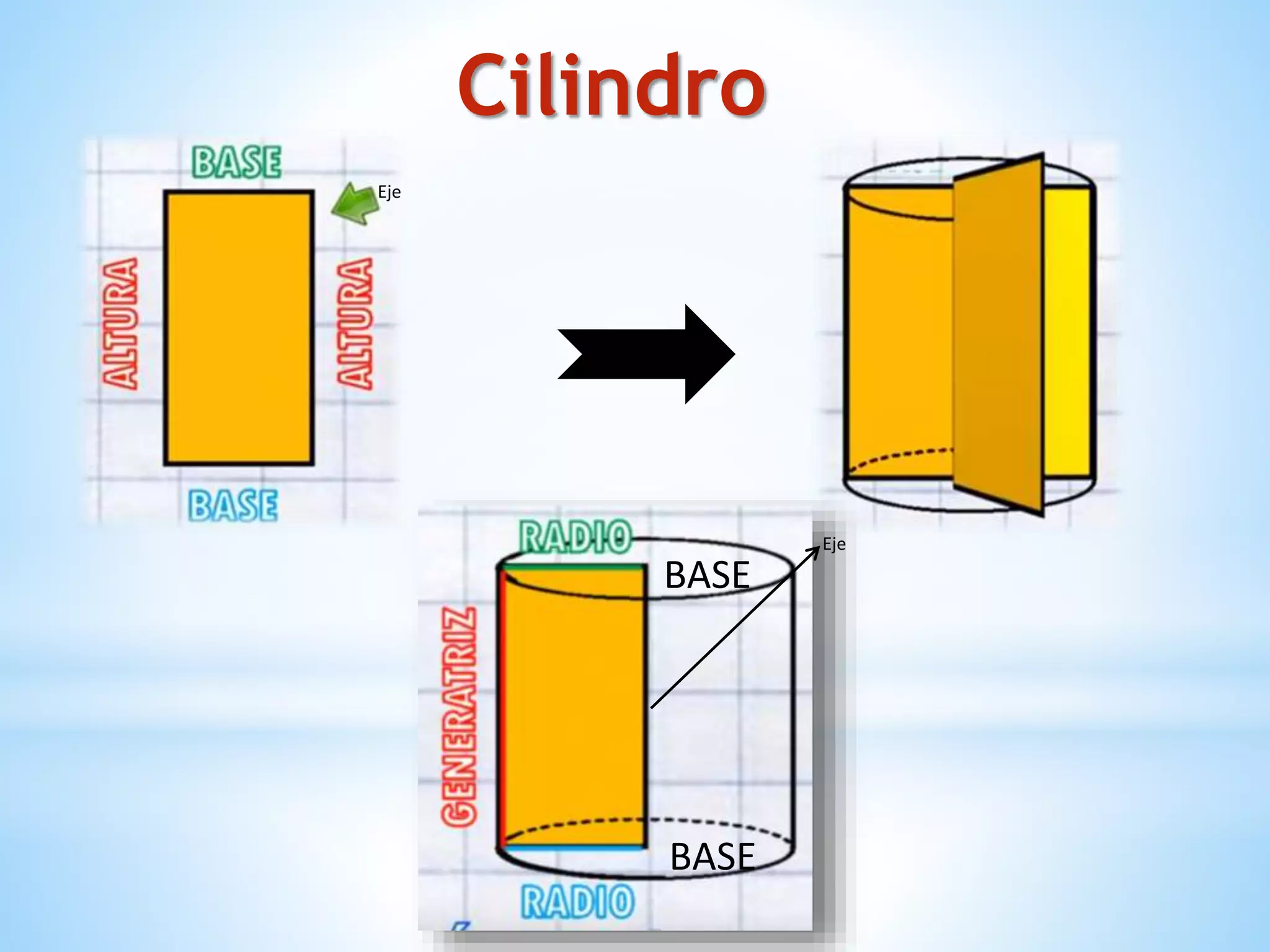
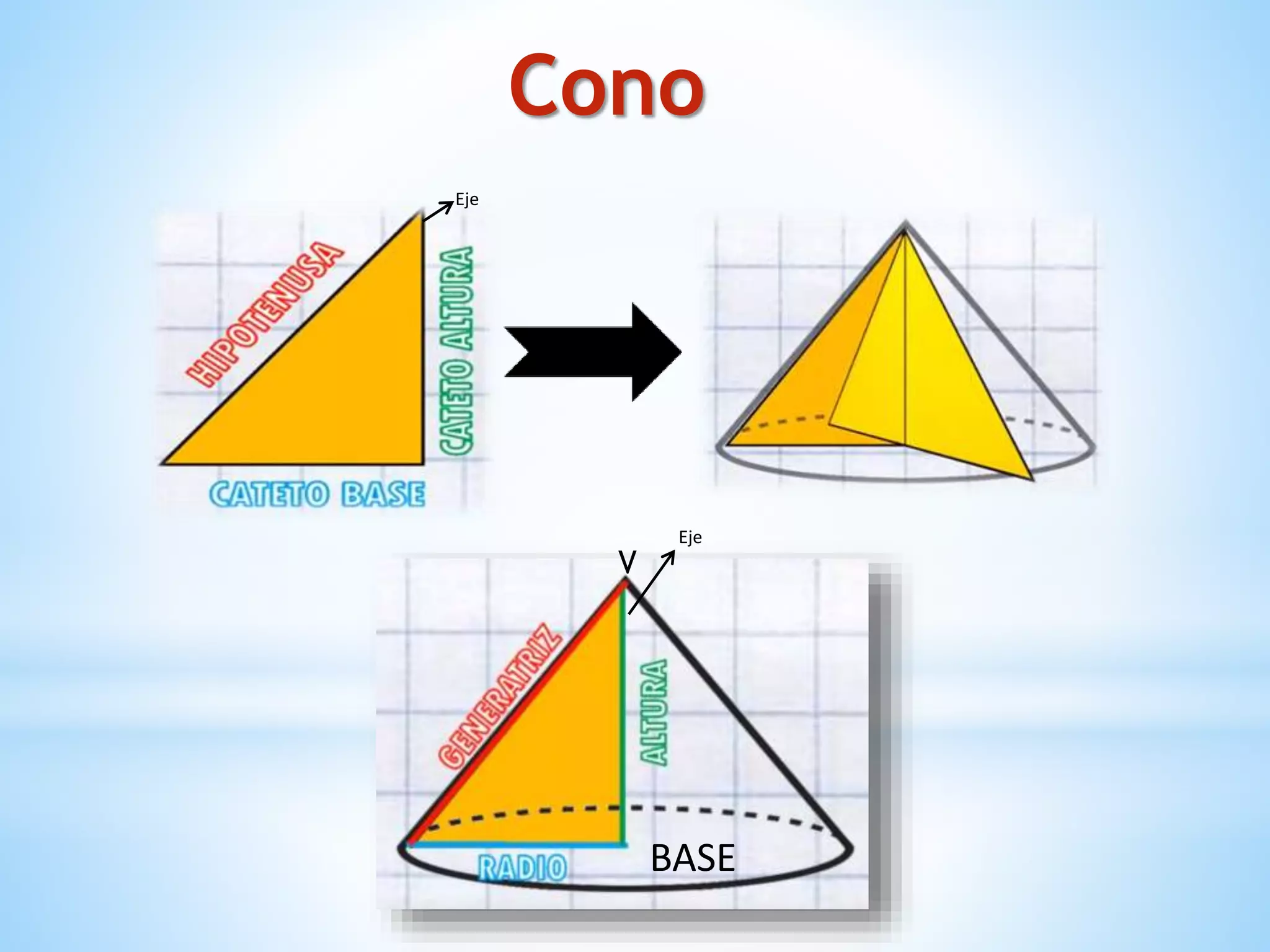
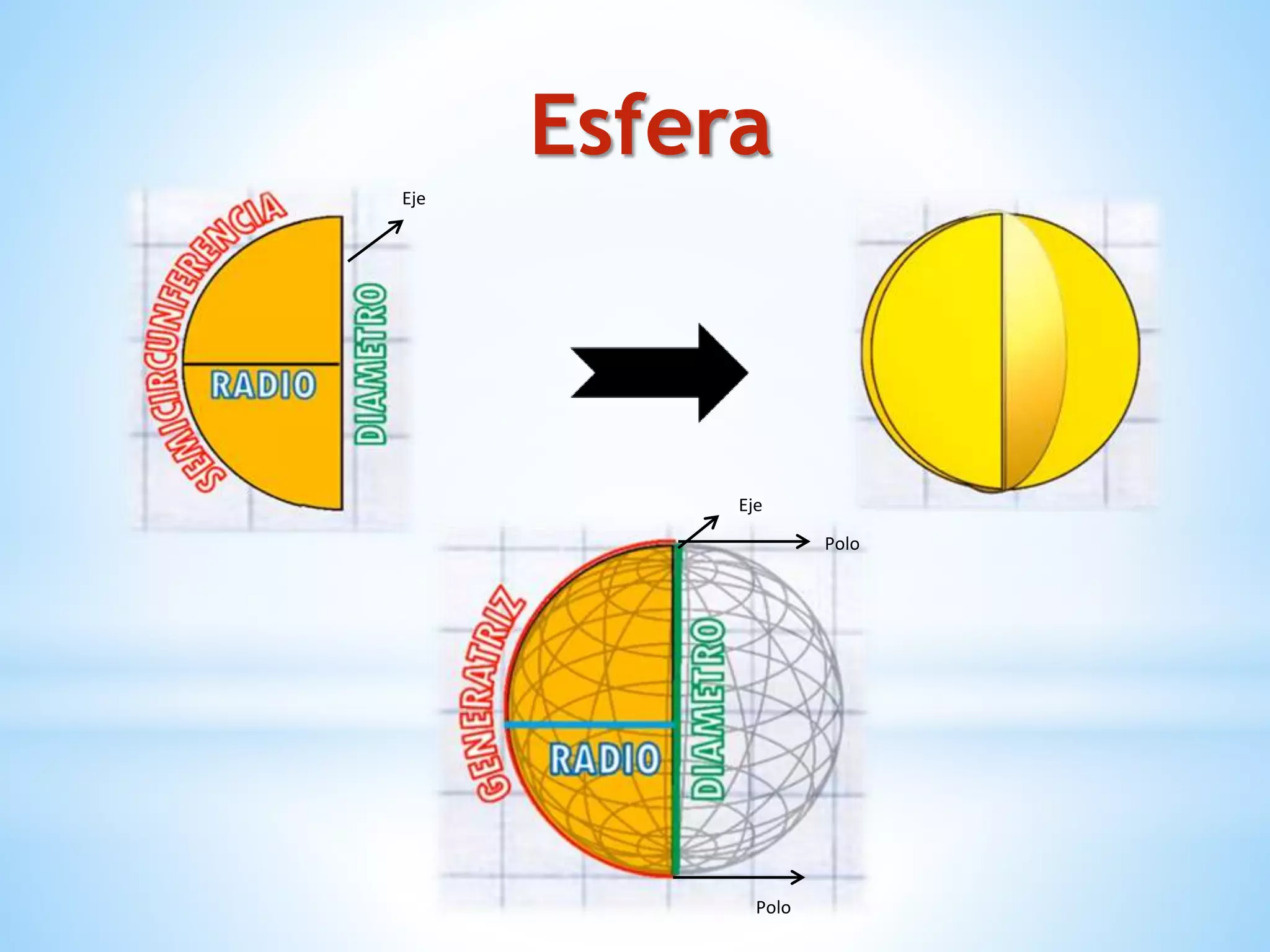
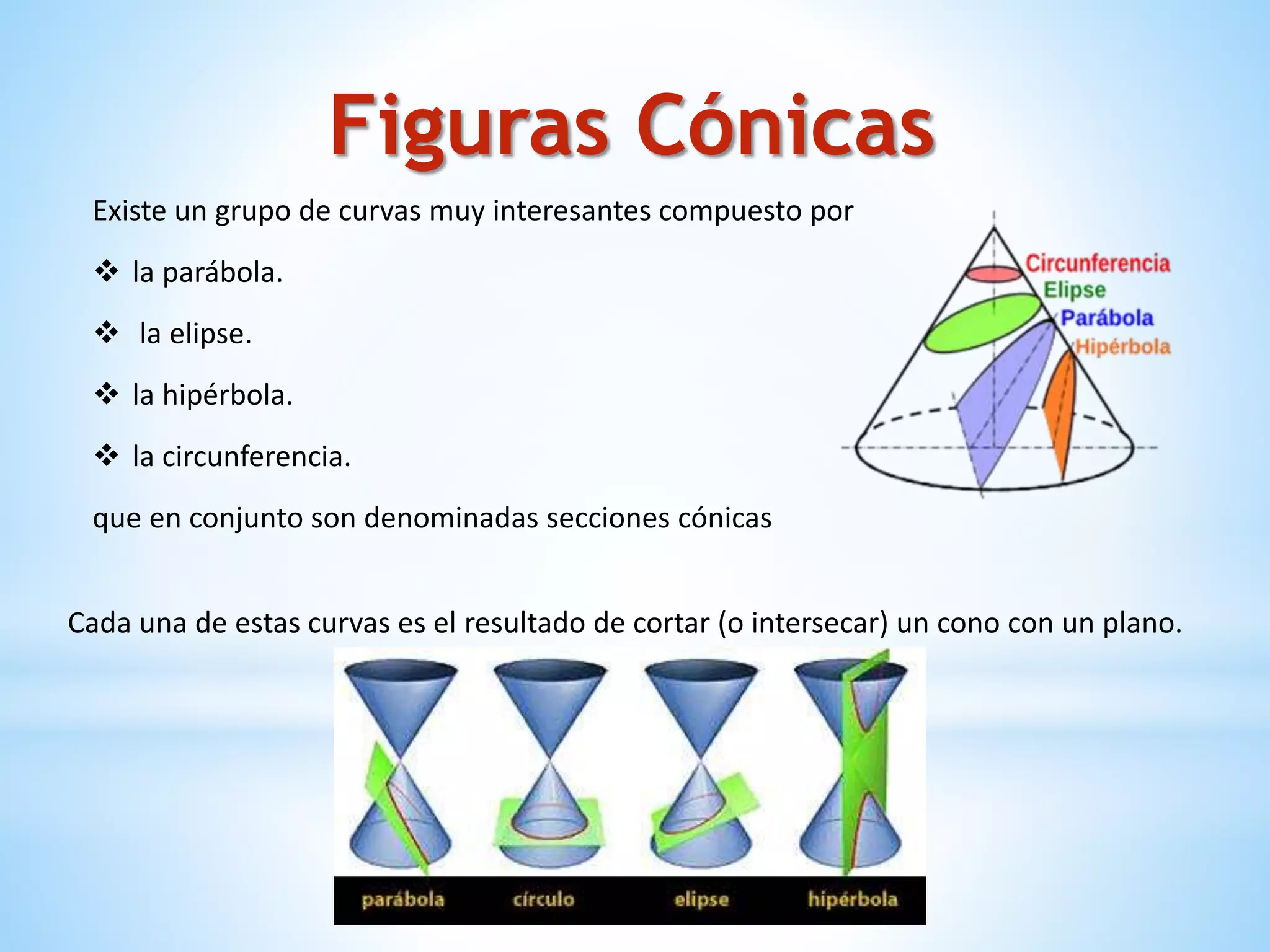
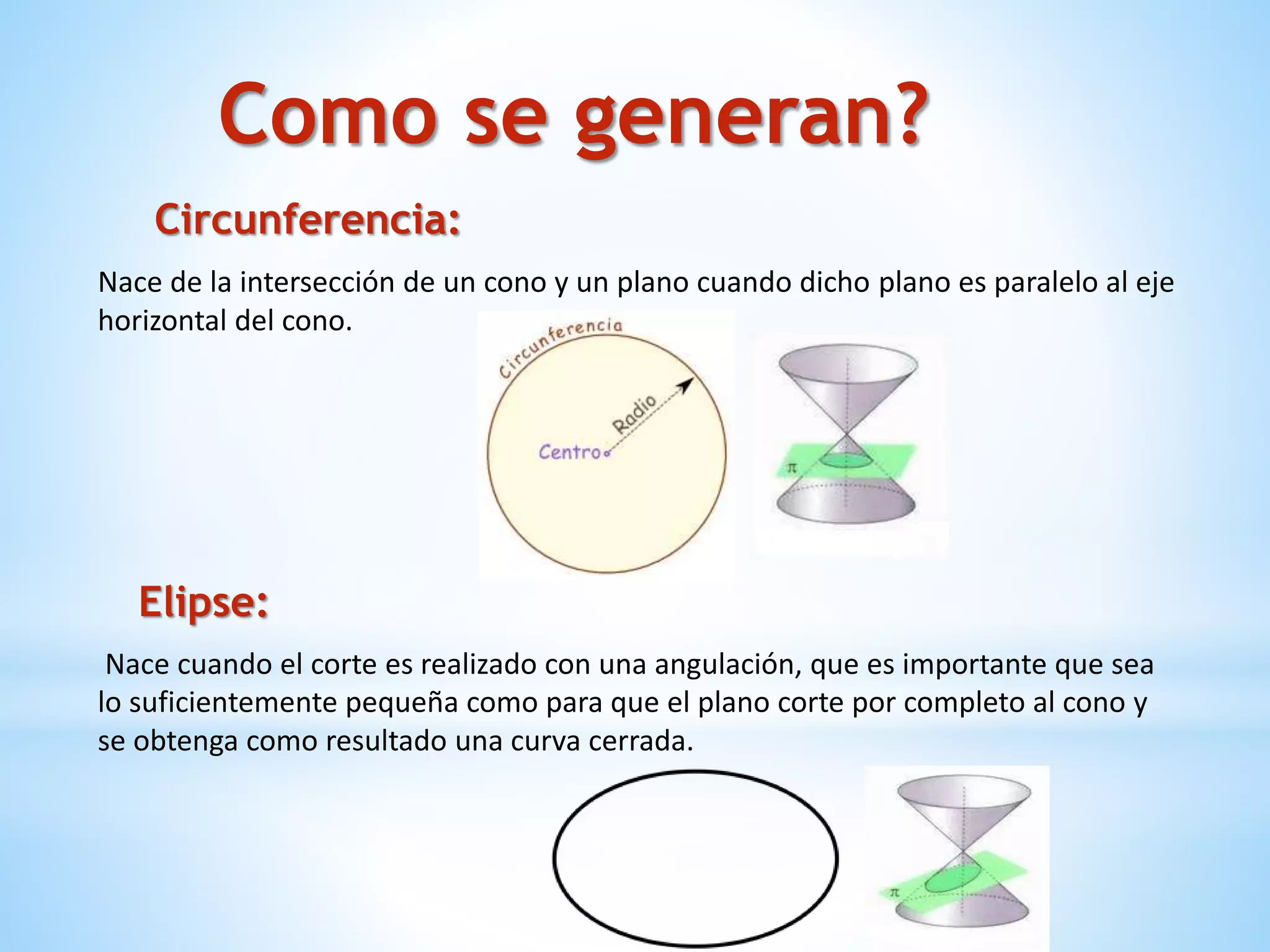
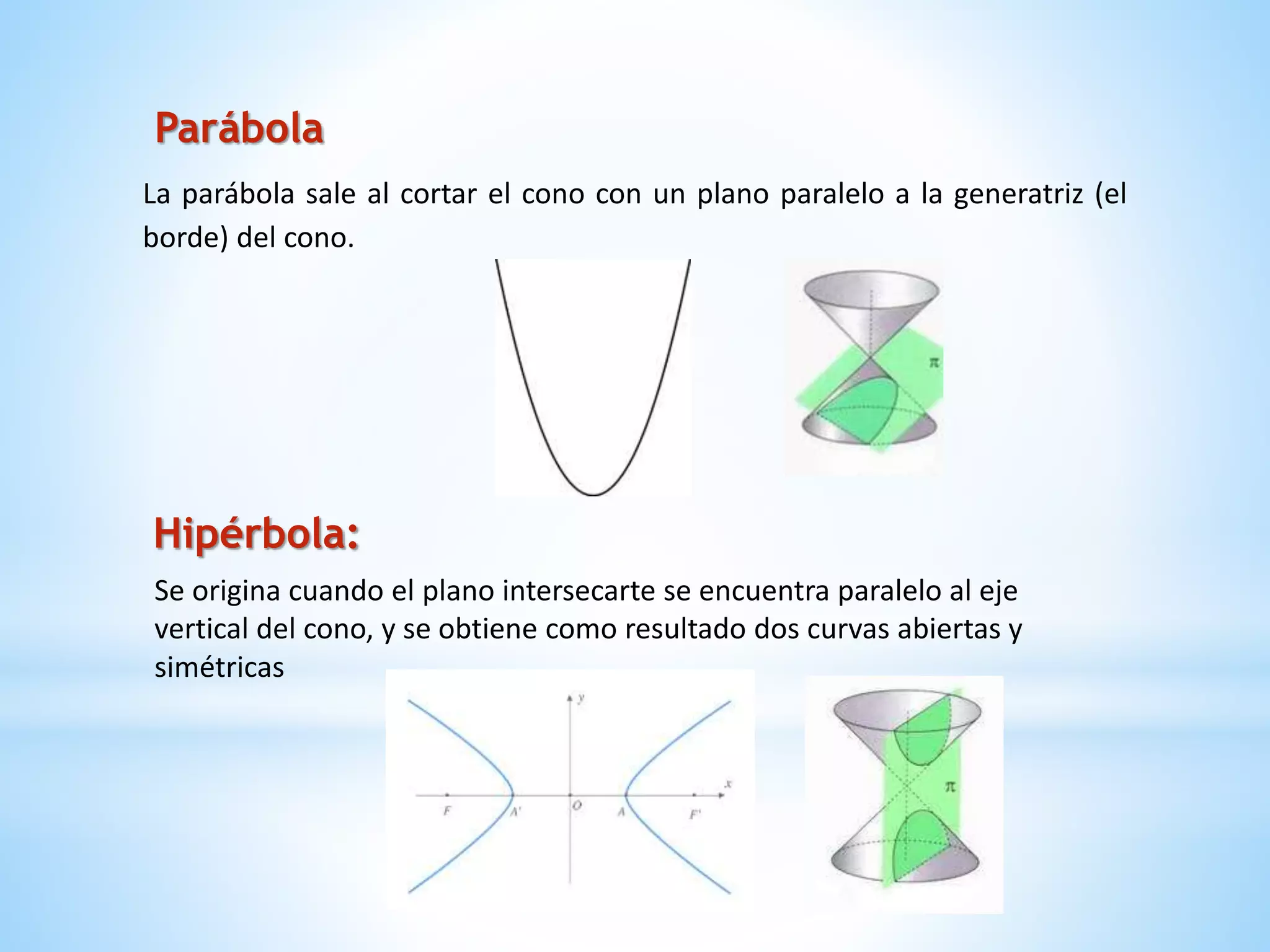
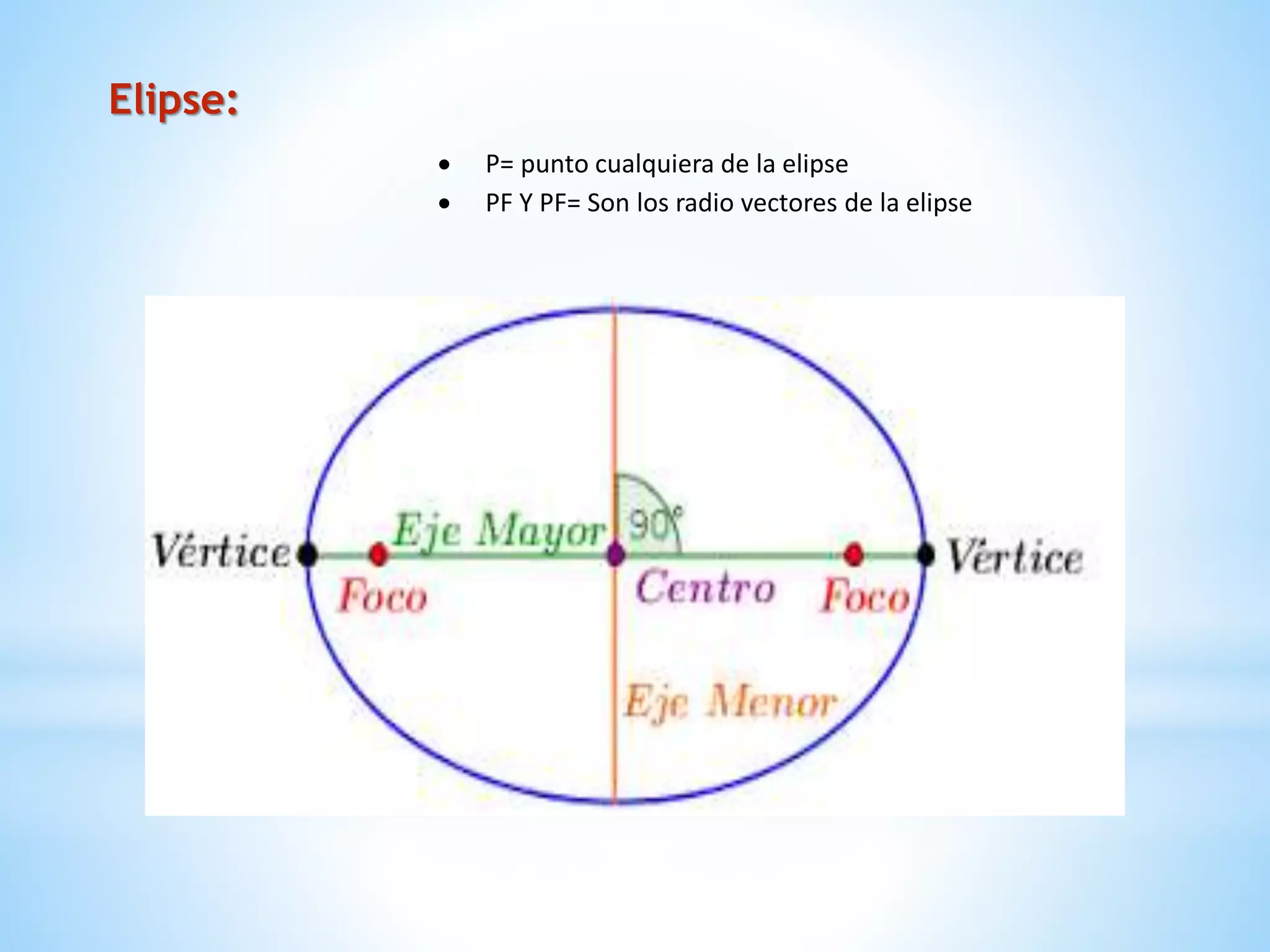
El documento describe los cuerpos geométricos, incluyendo su definición como formas tridimensionales que ocupan un volumen, y cómo se calcula el volumen. Explica que los cuerpos de revolución más importantes son el cilindro, el cono y la esfera. También describe las figuras cónicas como curvas planas generadas por la intersección de un cono con un plano, incluyendo la circunferencia, elipse, parábola e hipérbola.

2. Un cuerpo geométrico es un
elemento que existe en la
realidad o que somos
capaces de concebir, el cual
ocupa un volumen en el
espacio, A diferencia de las
figuras las cuales no tienen
volumen.
Cuerpo geométrico

3.  El volumen de un
cuerpo es la cantidad
de espacio que ocupa
una forma en un lugar
 se obtiene al multiplicar tres
longitudes: largo, ancho y altura
Volumen

4. Diferencia entre
cuerpo y volumen
Entre cuerpo geométrico y volumen no hay ninguna diferencia por que para que uno
exista necesita del otro, es decir no puede haber un cuerpo si no hay volumen.
Utilidad de calcular volumen

5. Solidos de revolución
Los cuerpos de revolución son los cuerpos geométricos que se forman al
girar una figura plana alrededor de un eje.
Los tres cuerpos de revolución más importantes son:
 el cilindro.
 el cono
 la esfera

6. Cilindro
Eje
Eje
BASE
BASE

7. Cono
Eje
Eje
BASE
V

8. Esfera
Eje
Polo
Polo
Eje

9. Figuras Cónicas
Existe un grupo de curvas muy interesantes compuesto por
 la parábola.
 la elipse.
 la hipérbola.
 la circunferencia.
que en conjunto son denominadas secciones cónicas
Cada una de estas curvas es el resultado de cortar (o intersecar) un cono con un plano.

10. Como se generan?
Nace de la intersección de un cono y un plano cuando dicho plano es paralelo al eje
horizontal del cono.
Circunferencia:
Elipse:
Nace cuando el corte es realizado con una angulación, que es importante que sea
lo suficientemente pequeña como para que el plano corte por completo al cono y
se obtenga como resultado una curva cerrada.

11. Parábola
La parábola sale al cortar el cono con un plano paralelo a la generatriz (el
borde) del cono.
Hipérbola:
Se origina cuando el plano intersecarte se encuentra paralelo al eje
vertical del cono, y se obtiene como resultado dos curvas abiertas y
simétricas

12. Elementos de las figuras cónicas
Circunferencia:

13. Elipse:
 P= punto cualquiera de la elipse
 PF Y PF= Son los radio vectores de la elipse

14. Parábola
F= Foco
P= Parámetro
V= Vértice
AB= longitud del lado recto

15. Hipérbola:
Y: Es el eje secundario de la hipérbola y
es la matriz del deje focal.
X: es el eje focal de la hipérbola
F Y F’: Son los focos de la hipérbola
O: Es el centro de la hipérbola
P: es un punto de la hipérbola
PF Y PF: son los radio vectores de la
hipérbola
A Y A: son los vértices de la hipérbola

16. Alumnos: Perrone Sol, Agustina Montaldo,
Luna Ana Luz.
Profesor/a: Charras Mariana.
Institución: I.D.A.M.
Curso: 5to.
Materia: Matemática.
Tema: Geometría.
FIN