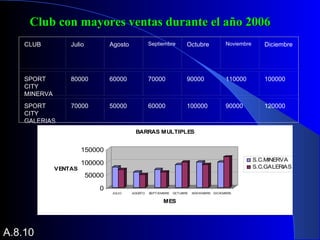
Este documento define qué es una gráfica y sus funciones principales como representar datos estadísticos y relaciones entre variables. Luego describe varios tipos de gráficas como barras, sectores, dispersión e histograma. Finalmente, explica los pasos para crear una gráfica como seleccionar los datos, elegir un tipo de gráfica e incluir títulos y etiquetas en los ejes.

1. ¿QUE ES UNA GRAFICA?
Un grafico o diafragma en estadística, es una especie de
esquemático, formado por líneas, figuras, mapas, utilizado para
representar datos estadísticos a escala o según una cierta pro-
porción, o bien los elementos de un sistema, las etapas de un
proceso y las divisiones o subdivisiones de una clasificación.
A.8.1

2. FUNCIONES DE LAS GRAFICAS:
Pueden evidenciar las relaciones entre los diversos ele-
mentos de un sistema o de un proceso y representar la
correlación entre dos o más variables.
Sistematizan y sintetizan los datos, sistemas y procesos.
Aclaran y complementan las tablas y las exposiciones
teóricas o cuantitativas.
El estudio de su disposición y de las relaciones que
muestran pueden sugerir hipótesis nuevas.
A.8.2

3. ESTADISTICAS PRINCIPALES:
 Gráfica en árbol.
 Gráfica de áreas o
superficies.
 Gráfica de bandas.
 Gráfica de barras.
 Gráfica de bloques.
 Gráfica circular.
 Gráfica circular polar.
A.8.3

4.  Gráfica de puntos ó polígono de frecuencia.
 Gráfica de tallo y hoja diagrama
 Histogramas y gráficos de caja y bigote o boxplots.
 Gráficos univariados.
A.8.4

5. Gráficos de puntos ó polígono de frecuencias: Es una
variación del diagrama líneal simple el cual esta formado
por líneas rectas o curvas, que resultan de la representación,
en un eje de coordenadas, de distribuciones de frecuencias.
Ejemplo: La siguiente distribución de frecuencia muestra los
valores acerca del porcentaje de grasa corporal de 520
deportistas.
A.8.5
INTERVALOS P.M. FRECUENCIA
5 - 9.99 7,5 12
10 - 14.9 12,5 120
15 - 19.9 17,5 180
20 - 24.9 22,5 140
25 - 29.9 27,5 50
30 - 34.9 32,5 18
POLIGONO DE FRECUENCIA
0
100
200
1 2 3 4 5 6
INTERVALOS
DEPORTISTAS
FRECUENCIA

6. Gráficos de tallo y hoja diagrama: es una forma rápida
de obtener una representación visual ilustrativa del conjunto
de datos, se debe seleccionar uno ó más dígitos iniciales para
los valores de tallo, el dígito o dígitos finales se convierten en
hojas, luego se hace una lista de valores de tallo en una
columna vertical.
A.8.6

7. Ejemplo: realice un diagrama de tallo y hoja para los
siguientes datos de las 10 mejores marcas de decatlón
hombres hasta Enero de 2006.
A.8.7
90 26
89 94
88 91 47 32 20 15
87 92 84 62

8. Diagramas de barras: nombre que recibe el diagrama
utilizado para representar gráficamente distribuciones
discretas de frecuencias no agrupadas.
Existen tres principales clases de gráficos de barras:
1. Barra simple. se emplean para graficar hechos únicos.
2. Barras múltiples. es muy recomendable para comprar
una serie estadística con otra.
3. Barras compuestas. en este método de graficación las
barras de la segunda serie se colocan encima de las
barras de la primera serie en forma respectiva.
A.8.8

9. El diagrama de barras proporciona información
comparativa principalmente y este es su uso principal,
este diagrama también muestra la información referente
a las frecuencias.
Ejemplo:
A.8.9
0
2
4
6
8
10
12
TITULOS
EQUIPOS
GUADALAJARA
AMERICA
CRUZ AZUL
TOLUCA
EQUIPOS TITULOS
GUADALAJARA 11
AMERICA 10
CRUZ AZUL 8
TOLUCA 8

10. CLUB Julio Agosto Septiembre Octubre Noviembre Diciembre
SPORT
CITY
MINERVA
80000 60000 70000 90000 110000 100000
SPORT
CITY
GALERIAS
70000 50000 60000 100000 90000 120000
A.8.10
Club con mayores ventas durante el año 2006Club con mayores ventas durante el año 2006
0
50000
100000
150000
VENTAS
JULIO AGOSTO SEPTIEMBRE OCTUBRE NOVIEMBRE DICIEMBRE
MES
BARRAS MULTIPLES
S.C.MINERVA
S.C.GALERIAS

11. BARRAS COMPUESTAS
0
50000
100000
150000
200000
250000
JULIO
AGOSTO
SEPTIEMBRE
OCTUBRE
NOVIEMBRE
DICIEM
BRE
MES
VENTAS
S.C.GALERIAS
S.C.MINERVA
A.8.11

12. Histograma: Se usa para representar variables
cuantitativas continuas que han sido agrupadas en
intervalos de clase.
Ejemplo: Estaturas de los socios de la alberca SC
Minerva.
A.8.12
INTERVALOS P.M. FREC
1.55 - 1.59 157,5 10
1.60 - 1.64 162,5 35
1.65 - 1.69 167,5 60
1.70 - 1.74 172,5 110
1.75 - 1.79 177,5 95
1.80 - 1.84 182,5 45
1.84 - 1.89 187,5 5
Atletas 360
ESTATURAS
0
20
40
60
80
100
120
1.55 -
1.59
1.60 -
1.64
1.65 -
1.69
1.70 -
1.74
1.75 -
1.79
1.80 -
1.84
1.84 -
1.89
ATLETAS

13. Diagramas de caja o boxplots: se usa cuando se
necesita la mayor información acerca de la distribución
de los datos.
Ejemplo:
Para los siguientes datos realice un diagrama de caja:
2.68 3.06 4.31 4.71 5.71 5.99 6.06 7.04 7.17 7.46 7.50 8.27
8.42 8.73 8.84 9.14 9.19 9.21 9.39 11.28 15.19 21.06
A.8.13

14. Gráficos de sectores (pastel): Es un gráfico que se basa
en una proporcionalidad entre la frecuencia y el ángulo
central de una circunferencia, de tal manera que a la
frecuencia total le corresponde el ángulo central de 360°.
Para construir se aplica la siguiente formula:
X = frecuencia relativa * 360°/S frecuencia relativa
A.8.14

15. Frecuencia 1 4 3 5 4
Deporte Atletism
o
Fútbol Béisbol Karate Natació
n
Tenis
Ejemplo: Representar mediante un gráfico de sectores la
frecuencia con que aparece cada disciplina deportiva que
eligieron 23 alumnos. Lo anterior se describe en la siguiente
distribución de frecuencias para datos cualitativos:
6
A.8.15
Deportes
1
2
3
4
5
6
Atletismo Fútbol
Beisbol
Karate
Natación
Tenis

16. Diagrama de dispersión: es un diagrama que
representa gráficamente, en un espacio de ordenadas,
este también se utiliza para el análisis de regresión.
Ejemplo:
X Y
A 2 3
B 4 1
C 5 4
D 3 6
E 2 8
A.8.16

17. Pasos a seguir para la realización de una grafica.
Selecciona los datos que quieres representar
•Haz clic en el botón para insertar la grafica.
•Has clic en la grafica que quieras insertar en tu
hoja (tipos de graficas mas adelante).
•Has clic en siguiente.
•En el siguiente paso, omítelo (2/4).
A.8.17

18. •En el paso 3 de 4 puedes incluir un titulo y ponerle
etiquetas a los ejes X e Y.
•En el ultimo paso solamente tienes que especificar
si quieres poner la grafica en la misma hoja o en una
nueva.
A.8.18