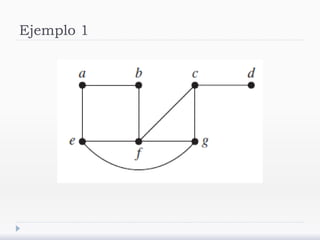
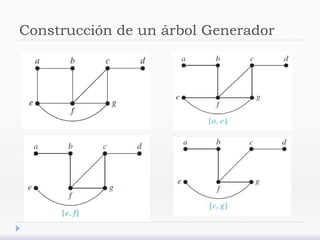
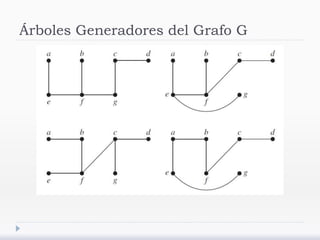
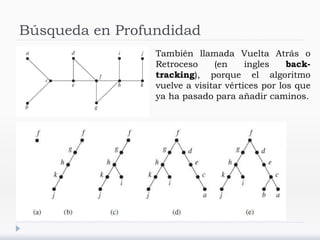
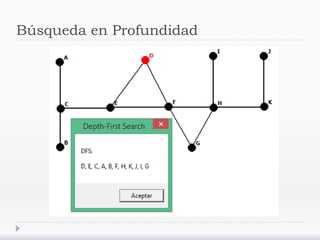
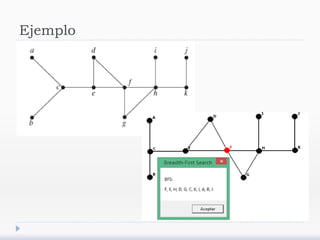
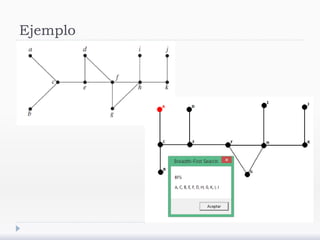
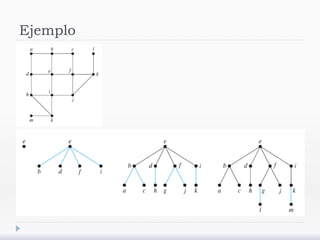
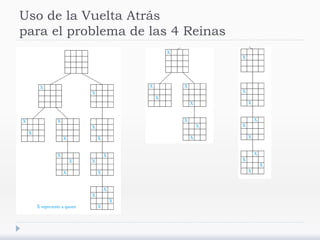
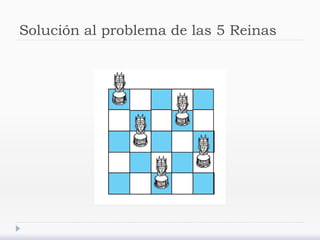
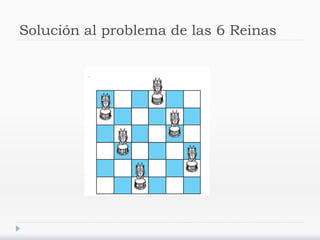
El documento describe árboles generadores y algoritmos para construirlos. Define un árbol generador como un subgrafo de un grafo simple que es un árbol y contiene cada vértice del grafo. Explica que los grafos deben ser conexos para admitir árboles generadores y presenta algoritmos de búsqueda en profundidad y anchura para construirlos.

1. Sección 9.4
Árboles Generadores
Tomado de Matemáticas Discretas y sus Aplicaciones. Rosen
Esteban Andrés Díaz Mina

2. Definición 1
 Sea G un grafo simple. Un árbol generador de G
es un subgrafo de G que es un árbol y contiene
cada vértice de G.
 Un grafo simple que admite un árbol generador
necesariamente debe ser conexo, puesto debe
existir un camino entre cualquier par de
vértices del árbol generador.

3. Ejemplo 1

4. Construcción de un árbol Generador

5. Árboles Generadores del Grafo G

6. Algoritmos para Construir
Árboles Generadores
 El algoritmo para obtener árboles generadores
mediante la supresión de aristas de los
circuitos simples de un grafo no es eficiente,
puesto que requiere identificar los circuitos
simples de algún modo.
 En lugar de construir árboles generadores
eliminando aristas, los árboles generadores se
pueden obtener añadiendo aristas.
 Presentamos dos algoritmos basados en esta
estrategia.

7. Búsqueda en Profundidad
 Podemos construir un árbol generador para un
grafo simple conexo utilizando una búsqueda
en profundidad.
 Se enuncia el procedimiento a través de un
ejemplo.

8. Búsqueda en Profundidad
También llamada Vuelta Atrás o
Retroceso (en ingles back-
tracking), porque el algoritmo
vuelve a visitar vértices por los que
ya ha pasado para añadir caminos.

9. Búsqueda en Profundidad

10. Búsqueda en Anchura
 También podemos generar un árbol generador
de un grafo simple mediante la búsqueda en
anchura o por niveles.
 Se enuncia el procedimiento a través de un
ejemplo.

11. Ejemplo

12. Ejemplo

13. Ejemplo

14. Aplicaciones de la Vuelta Atrás
Hay problemas que se pueden resolver realizando
una búsqueda exhaustiva de todas las soluciones
posibles. Un método de búsqueda sistemática de una
solución es utilizar un árbol de decisión, donde cada
vértice interno representa una decisión y cada hoja
una posible solución. Para encontrar una solución
mediante la Vuelta atrás, primero construimos una
secuencia de decisiones intentando alcanzar una
solución mientras sea posible.

15. Aplicaciones de la Vuelta Atrás
Esta serie de decisiones se puede representar por un
camino en el árbol de decisión. Una vez que se sabe
que no existe solución en las hojas que son
descendientes del vértice que se está procesando, se
vuelve atrás hacia el padre del vértice en curso y se
trabaja en la búsqueda de soluciones realizando otra
serie de decisiones.
El procedimiento continúa hasta que se consigue una
solución o se establece que tal solución no existe.

16. El problema de la n Reinas
El problema de las n reinas consiste en determinar
cómo se pueden colocar n reinas en el tablero de
ajedrez n x n de manera que dos reinas cualesquiera
no puedan amenazarse mutuamente. ¿Cómo se
puede utilizar la vuelta atrás para resolver el
problema de las n reinas?.
Ver descripción de la solución en el libro. Pagina 635.

17. Uso de la Vuelta Atrás
para el problema de las 4 Reinas

18. Solución al problema de las 5 Reinas

19. Solución al problema de las 6 Reinas

20. Solución al problema de las 8 Reinas
Consulte
http://es.wikipedia.org/wiki/Problema_de_las_ocho_reinas

21. Problemas Propuestos
Problemas Sección 9.4
4 7 14
16 17 18