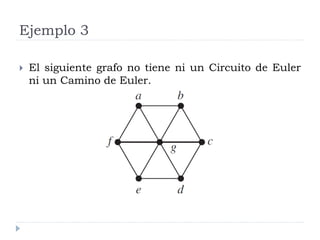
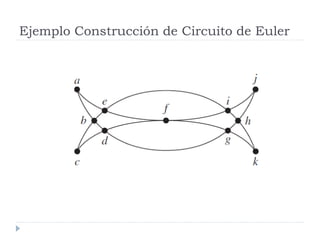
Este documento discute caminos Eulerianos y Hamiltonianos en grafos. Explica que un camino Euleriano visita cada arista exactamente una vez mientras que un camino Hamiltoniano visita cada vértice exactamente una vez. Mientras que la existencia de un camino Euleriano depende de que todos los vértices tengan grado par, determinar si un grafo tiene un camino Hamiltoniano es mucho más difícil. El documento también provee ejemplos y algoritmos para identificar estos caminos.

1. Caminos Eulerianos y Hamiltonianos
Tomado de Matemáticas Discretas y sus Aplicaciones. Rosen
Esteban Andrés Díaz Mina

2. Introducción
 ¿Podemos movernos por las aristas de un grafo
comenzando en un vértice y volviendo a él después
de haber pasado por cada arista del grafo
exactamente una vez?
 Análogamente, ¿podemos desplazarnos por las
aristas de un grafo comenzando en un vértice y
volviendo a él después de haber visitado cada
vértice del grafo exactamente una vez?

3. Introducción
 Aunque estas preguntas parecen similares, la
primera de ellas, que pregunta si el grafo tiene lo
que se llama un circuito euleriano, puede
resolverse fácilmente para cualquier grafo, mientras
que la segunda cuestión, la de si el grafo tiene o no
lo que se llama un circuito hamiltoniano, es
bastante difícil de resolver.

4. Introducción
 En esta sesión analizaremos ambas preguntas y
estudiaremos las dificultades que se presentan a la
hora de resolverlas.
 Aunque ambas preguntas tienen muchas
aplicaciones practicas en diferentes áreas, ambas
surgieron a partir de antiguos pasatiempos.

5. Caminos y Circuitos de Euler
 Reseña histórica: la ciudad de Konigsberg (Prusia) fue
dividida en cuatro partes por los riachuelos del río
Praga. Esas cuatro secciones fueron unidas por siete
puentes. Los ciudadanos tomaban largas caminatas los
domingos. Ellos se preguntaron si era posible iniciar en
un sitio, cruzar por todos los puentes una sola vez, y
regresar al punto de partida.

6. Teoremas
 Esta inquietud fue resuelta por el matemático suizo
Leonard Euler en el siglo XVIII.
Teorema 1
Un multigrafo conectado tiene un circuito Euler si y
solo si cada vértice tiene grado par.
Teorema 2
Un multigrafo conectado tiene un camino Euler pero
no un circuito Euler si y solo si tiene exactamente 2
vértices de grado impar.

7. Definición 1
 Un circuito Euler en un grafo G es un circuito simple
que contiene cada arista de G.
 Un camino Euler en G es un camino simple que
contiene cada arista en G.

8. Ejemplo 1
 El siguiente grafo tiene un Circuito de Euler.

9. Ejemplo 2
 El siguiente grafo tiene un Camino de Euler pero no
un Circuito de Euler

10. Ejemplo 3
 El siguiente grafo no tiene ni un Circuito de Euler
ni un Camino de Euler.

11. Ejemplo 4
 El siguiente grafo no tiene ni un Circuito de Euler
ni un Camino de Euler.

12. Algoritmo 1

13. Ejemplo Construcción de Circuito de Euler

14.  Reseña histórica: Todo inicia en un acertijo
inventado por el matemático irlandés William
Hamilton. Consistía de un dodecaedro (poliedro con
12 pentágonos regulares como caras) de madera
con alfileres con nombres de ciudades en cada
vértice. Los 20 vértices se marcaron con 20
ciudades del mundo. El objetivo era iniciar en una
ciudad y viajar a través de las aristas visitando
cada una de las otras 19 ciudades solo una vez, y
regresar a la primera ciudad.
Caminos y Circuitos de Hamilton

15. Definición 1

16. Definición 1
 Un camino x0, x1,...., xn-1, xn en el grafo G=(V,E) es
llamado un camino Hamilton si V={x0, x1,...., xn-1, xn} y
xi≠xj para 0≤i<j≤n.
 Un circuito x0, x1,...., xn-1, xn , x0 (con n>1) en un grafo
G=(V,E) es llamado un circuito Hamilton si
x0, x1,...., xn-1, xn es un camino Hamilton.

17. Ejemplo 1
 Grafica con Circuito de Hamilton

18. Ejemplo 2
 Grafica con Camino de Hamilton

19. Ejemplo 3
 Grafica sin camino Hamiltoniano

20. Ejemplo 3
Dos de las condiciones suficientes más importantes para que un
grafo sea un circuito de Hamilton son:
Teorema 1 (Teorema de DIRAC’S)
Si G es un grafo simple con n vértices con n≥3 tal que el grado
de cada vértice en G es al menos n/2, entonces G tiene un
circuito Hamilton.
Teorema 2 (Teorema de ORE’S)
Si G es un grafo simple con n vértices con n≥3 tal que
g(u)+g(v)≥n para cada par de vértices no adyacentes u y v en G,
entonces G tiene un circuito Hamilton.


21. Finalizamos
Caminos
Eulerianos y Hamiltonianos
Hasta pronto