El documento describe los operadores lógicos y cómo se usan para unir proposiciones. Explica los conectivos lógicos como "y", "o", "si...entonces", etc. y provee ejemplos de cómo se usan. También distingue entre proposiciones atómicas y moleculares, y describe tablas de verdad y cómo determinar el valor de verdad de proposiciones compuestas.

1. Gregory Cordero
C.I. 14.879.114
SAIA B
Noviembre 2012
Cabudare-Edo. Lara

6. Operaciones Veritativas:
Los Conectivos u Operadores Lógicos son símbolos o
conectivos que nos permiten construir otras proposiciones; o
simplemente unir dos o más proposiciones, a partir de
proposiciones dadas. Se le llama conectivos lógicos a los
conectivos: y; o; o…o; si,.. Entonces; sí y sólo si; no ;
Ejemplo: p: Marte es un planeta ; q: el sol es una estrella.
1)Marte es un planeta y el sol es una estrella.
2)O Marte es un planeta o el sol es una estrella.
3)Marte es una estrella sí y sólo si el sol es una estrella.

7. NOTA IMPORTANTE: Cuando una proposición no contiene
conectivos lógicos diremos que es una proposición atómica o
simple; y en el caso contrario, diremos que es una proposición
molecular o compuesta.
Proposición atómica o simple:
1) Marte es un planeta
2) El sol es una estrella
proposición molecular o compuesta:
1)Marte es un planeta y el sol es una estrella.
2)O Marte es un planeta o el sol es una estrella.
3)Marte es una estrella sí y sólo si el sol es una estrella.

8. TABLA SIMBOLICA

9. La negación
Sea p una proposición, la negación de p es otra
proposición identificada por: ~ p, que se lee "no p", "no es
cierto que p", "es falso que p", y cuyo valor lógico está
dado por la siguiente tabla de verdad.
Ejemplo: p: Barcelona es un estado Oriental.
~ p: Es falso que Barcelona es un estado Oriental.
~ p: No es cierto que Barcelona sea un estado Oriental.
~ p: Barcelona no es un estado Oriental.

10. La conjunción
Sean p y q dos proposiciones. La conjunción de p y q es
la proposición p ^ q, que se lee "p y q", y cuyo valor lógico
está dado con la tabla o igualdad siguiente:
Ejemplo:
p: el negro primero peleo en Carabobo.
q: Bolívar murió en Colombia.
p ^ q: El Negro Primero peleó en Carabobo y Bolívar murió en
Colombia.
Además, VL(p ^ q) = 1, ya que VL(p)= 1 y VL(q)= 1.

11. La disyunción inclusiva
Sean p y q dos proposiciones. La disyunción de p y q es
la proposición p v q, que se lee "p o q", y cuyo valor lógico
está dado por la tabla siguiente:
Ejemplo:
p: La estatua de la Divina Pastora está en Barquisimeto
q: La estatua de Miranda está en Caracas.
p v q: La estatua de la Divina Pastora está en Barquisimeto o La
estatua de Miranda está en Caracas.
VL(pvq)=1, ya que VL(p)=1 y VL(q) = 0.

12. La disyunción exclusiva
Sean p y q dos proposiciones. La disyunción
exclusiva de p y q es la proposición pvq, que se lee "o p o
q", y cuyo valor lógico está dado por la tabla.
Ejemplo: p: 17 es un número primo; q: 17 es un número par
p v q: ó 17 es un número primo ó 17 es un número par.
VL(p v q) = 1, ya que VL(p) = 1 y VL(q) = 0.

13. El condicional
Sean p y q dos proposiciones. El condicional con
antecedente p y consecuente q es la proposición p →q, que se
lee "si p, entonces q", y cuyo valor lógico está dado por la
siguiente tabla:
Ejemplo:
Observe las proposiciones condicionales siguientes:
1. Si 5 es primo, entonces 2 + 1 = 3 (Verdadera).
2. Si 5 es primo, entonces 2 + 1 = 4 (Falsa).

14. Condicionales Asociados
Dado un condicional p→q podemos asociarles los
siguientes condicionales:
1. Directo: p →q
2. Recíproco: q →p
3. Contrarrecíproco: ~ q → ~ p
4. Contrario: ~ p → ~ q

15. Ejemplo
Escribir el recíproco, contrarrecíproco y contrario del
siguiente condicional: Si 5 es primo entonces 7 es impar.
Solución
* Recíproco: Si 7 es impar entonces 5 es primo.
* Contrario: Si 5 no es primo entonces 7 no es impar.
* Contrarrecíproco: Si 7 no es impar entonces 5 no es primo.

16. El Bicondicional
Sean p y q dos proposiciones. Se llama Bicondicional
de p y q a la proposición p↔q, que se lee "p si sólo si q", o "p
es condición necesaria y suficiente para q", y cuyo valor lógico
es dado por la siguiente tabla.
La tabla nos dice que p↔q es verdadero cuando VL(p) = VL(q),
y esa falsa cuando VL(p) ≠VL(q)
Ejemplo: p: 2 + 1 = 3 ; q: 2< 3
p↔q : 2 + 1 = 3 si y sólo si 2< 3

17. Formas Proposicionales
A las nuevas expresiones que se obtienen al aplicar los
conectivos lógicos a las variables proposicionales p, q, r, s, t,
entre otros., se les llaman formas proposicionales, por
ejemplo: t→ (q ^ ~ r) ~ [(p↔ s)^ (r↔ q)] son formas
proposicionales y podemos decir, para ser más preciso que las
variables proposicionales también son formas proposicionales.

18. Tablas de Verdad de las Formas Proposicionales
Las tablas de verdad permiten determinar el valor de verdad
de una proposición compuesta y depende de las proposiciones
simples y de los operadores que contengan.
Las posibilidades de combinar valores de verdad dependen del
número de proposiciones dadas.
Para una proposición (n = 1), tenemos 21 = 2 combinaciones
Para dos proposiciones (n = 2), tenemos 22 = 4 combinaciones
Para tres proposiciones (n = 3), tenemos 2 3 = 8 combinaciones
Para n proposiciones tenemos 2n combinaciones

19. Tautologías y Contradicciones
Proposición Tautológica o Tautología
Es aquella proposición molecular que es verdadera (es decir,
todos los valores en su conectivo principal de su tabla de verdad son
(1) independientemente de los valores de sus variables.
Ejemplo:
Probar que P v ~ P es una tautología
P v ~P
1 1 0
0 1 1

20. Contradicción
Es aquella proposición molecular que siempre es falsa (es decir
cuando los valores de su conectivo principal son todos 0)
independientemente de los valores de sus variables proposicionales que la
forman.
Por ejemplo, la proposición molecular del ejemplo siguiente es una
contradicción, p ^ ~ p, para chequearlo recurrimos al método de las tablas
de verdad.
Ejemplo: Probar que p ^ ~ p es una contradicción
pÙ~p
100
001

21. Leyes del Algebra de Proposiciones
Leyes Idempotentes
1.1. p ^ p =p
1.2. p v p = p
2.Leyes Asociativas
2.1. (P v q) v r =p v (q v r)
2.2. (P ^ q) ^r = p ^(q ^ r)
3. Leyes Conmutativas
3.1. P ^q = q ^p
3.2. P v q = q v p
4. Leyes Distributivas
4.1. P v ( q ^ r ) = ( p v q ) ^ (p v r)
4.2. P ^ ( q v r ) = ( p ^q ) v (p ^ r)
5. Leyes de Identidad
5.1. P v F =P
5.2. P ^ F = F
5.3. P v V = V
5.4. P ^ V =P

22. 6. Leyes de Complementación
6.1. P v ~ P = V (tercio excluido)
6.2. P ^ ~ P = F (contradicción)
6.3. ~ ~ P = P (doble negación)
6.4. ~ V = F, ~ F = V
Otras Equivalencias Notables
a. p→ q = ~ p v q (Ley del condicional)
b. p↔ q = (p→ q) ^ (q→ p) (Ley del bicondicional)
c. p v q = ( p ^ ~ q ) v ( q ^ ~ p ) (Ley de disyunción exclusiva)
d. p→ q = ~ q→ ~ p (Ley del contrarrecíproco)
e. p^q=~(~pv~q)
f. (p v q ) → r ) = ( p → r ) ^ (q → r ) (Ley de demostración por casos)
g. g. (p→ q) = (p ^ ~ q →F) (Ley de reducción al absurdo)

23. IMPORTANTE
Una de las grandes utilidades de las leyes dadas
anteriormente es que nos permiten simplificar proposiciones.
El procedimiento de probar que una proposición es
equivalente a otra usando las leyes del álgebra proposicional,
es llamada prueba deductiva.

24. Ejemplo
Probar deductivamente la ley de exportación
( p ^ q ) → r ) = ( p → (q → r )
Solución
( p ^ q ) → r = ~ ( p ^ q ) v r ( Ley condicional )
= (~ p v ~ q) v r ( Ley de De Morgan)
= ~ p v (~ q v r ) ( Ley asociativa )
= ~ p v (q → r) ( Ley condicional)
= p → (q → r) ( Ley condicional)

25. Circuitos Lógicos
Los circuitos lógicos o redes de conmutación los
podemos identificar con una forma proposicional. Es decir,
dada una forma proposicional, podemos asociarle un
circuito; o dado un circuito podemos asociarle la forma
proposicional correspondiente. Además, usando las leyes
del álgebra proposicional podemos simplificar los circuitos
en otros más sencillos, pero que cumplen la misma función
que el original.

26. Veamos los siguientes interruptores en conexión:
La conexión en serie: p^q
La conexión en paralelo: pvq

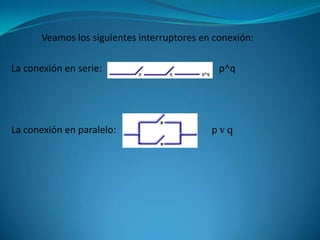
27. Ejemplo
Construir el circuito correspondiente a la siguiente
expresión:
(p ^ q) v [( p ^ r) v ~ s)]
Solución:

28. Ejemplo: Simplificar el siguiente circuito:
(p v q)^ (~ p v q)^ (~ p v ~ q)
= [(p v q)^ (~ p v q)] ^ (~ p v ~ q)
= [(p ^ ~ p) v q] ^ (~ p v ~ q)
= [F v q] ^ (~ p v ~ q)
= q ^ (~ p v ~ q)
= ( q ^ ~ p) v (q ^ ~ q)
= ( q ^ ~ p) v F
= ( q ^ ~ p) ; esto es equivalente a: