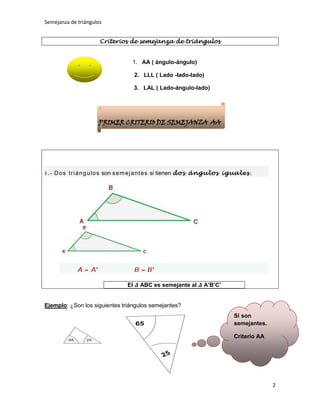
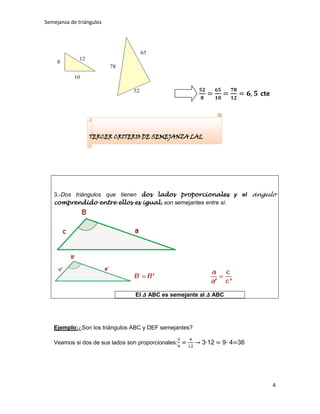
Este documento presenta los conceptos clave de la semejanza de triángulos. Explica que dos figuras son semejantes si tienen la misma forma pero no necesariamente el mismo tamaño. Detalla que para que dos triángulos sean semejantes, deben tener ángulos correspondientes iguales y lados correspondientes proporcionales. Finalmente, introduce tres criterios para determinar si dos triángulos son semejantes: criterio AA (ángulo-ángulo), criterio LLL (lado-lado-lado) y criterio LAL (l

1. Semejanza de triángulos
GUIA DE ESTUDIO
SEMEJANZA
Matemáticas - Primer Ciclo
Mónica Morales M. tutitapo@hotmail.com 19 de Octubre 2011
Nombre:……………………………………………………………………………………
I.- Concepto: dos figuras son semejantes cuando tienen la misma forma pero no
necesariamente el mismo tamaño.
II.-Definición geométrica: Dos figuras son semejantes cuando la razón entre las medidas
de sus lados homólogos (correspondientes) es constante, es decir son
proporcionales y sus ángulos correspondientes son congruentes.
Ejemplo: ¿Los siguientes rectángulos son semejantes?
6cm
8cm 4cm
12cm
¿Tiene sus lados respectivos proporcionales?.
II.- Triángulos semejante: Dos triángulos son semejantes si sus ángulos homólogos
son iguales y sus lados homólogos son proporcionales.
III.-Criterios de semejanza de triángulos. Existen algunos principios que nos permiten
determinar si dos triángulos son semejantes sin necesidad de medir y comparar todos
sus lados y todos sus ángulos. Estos principios se conocen con el nombre de criterios de
semejanza de triángulos
1

2. Semejanza de triángulos
Criterios de semejanza de triángulos
1. AA ( ángulo-ángulo)
2. LLL ( Lado -lado-lado)
3. LAL ( Lado-ángulo-lado)
PRIMER CRITERIO DE SEMEJANZA AA
1 . - D o s t r i á n g u l o s son s e m ej a nt e s si tienen d o s á n gu l o s i gua l e s .
El ABC es semejante al A’B’C’
Ejemplo: ¿Son los siguientes triángulos semejantes?
Si son
semejantes.
Criterio AA
2

3. Semejanza de triángulos
SEGUNDO CRITERIO DE SEMEJANZA LLl
2 . - D o s t r i á ng u l o s son s e m ej a nt e s si tienen los l a d o s p ro p o rc i o n a l e s .
El ABC es semejante al A’B’C’
E j e m p l o : C o n o c em o s l a s d i m e n s i o n e s d e l o s l a d o s d e d o s t r i á ng u l o s.
C o m p r u e b a s i s o n se m e j a nt e s y h a l l a l a r a zó n d e s em ej a n za .
a ) 8 c m , 1 0c m y 1 2 c m . b) 5 2c m , 65 c m y 7 8 c m .
Si son semejantes por
criterio LLL
Representemos el ejercicio:
3

4. Semejanza de triángulos
cte
TERCER CRITERIO DE SEMEJANZA LAL
3.-Dos triángulos que tienen dos lados proporcionales y el ángulo
comprendido entre ellos es igual, son semejantes entre sí.
El ABC es semejante al ABC
Ejemplo:¿Son los triángulos ABC y DEF semejantes?
Veamos si dos de sus lados son proporcionales: 3∙12 9∙ 4 36
4

5. Semejanza de triángulos
Si son semejantes
por criterio LAL
Bibliografía:
http://www.vitutor.com/geo/eso/ss_3.html
PPT de semejanza
5