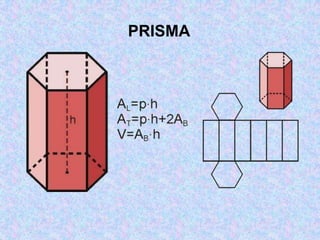
El documento clasifica diferentes tipos de triángulos y cuadriláteros según sus lados y ángulos. También describe elementos como las medianas, alturas y bisectrices de los triángulos, así como propiedades de figuras como paralelogramos, trapecios y el teorema de Pitágoras. Finalmente, introduce conceptos sobre polígonos, circunferencias, cuerpos geométricos en el plano y en el espacio.

2. TRIÁNGULOS
CLASIFICACIÓN DE TRIÁNGULOS SEGÚN SUS LADOS
Triángulo Equilátero: Tiene sus tres lados de igual medida.
Triángulo Isósceles: Tiene dos lados de igual medida.
Triángulo Escaleno: Tiene sus tres lados de distinta medida.

3. CLASIFICACIÓN DE TRIÁNGULOS SEGÚN SUS ÁNGULOS
Triángulo Acutángulo: Tiene sus tres ángulos agudos.
Triángulo Rectángulo: Tiene un ángulo recto.
Triángulo Obtusángulo: Tiene un ángulo obtuso.

4. Propiedad
La suma de los ángulos de un triángulo vale 180º
A + B + C = 180°

5. RECTAS Y PUNTOS NOTABLES DE LOS TRIÁNGULOS
MEDIANAS ALTURAS

6. MEDIATRICES BISECTRICES
Circunferencia
inscrita
ncentro

7. TRIÁNGULO RECTÁNGULO.
ELEMENTOS:
Hipotenusa: Lado mayor
Catetos: Lados menores

8. TEOREMA DE PITÁGORAS
En un triángulo rectángulo, el cuadrado de la hipotenusa
es igual a la suma de los cuadrados de los catetos.
a2 + b2 = c2

9. DEMOSTRACIÓN
c2 = a2 + b2

10. APLICACIONES DEL
TEOREMA DE PITÁGORAS
A) Calcular un lado de un triángulo rectángulo conocidos los otros dos
x = 6,71 m y = 8,66 cm z = 36,05 dm
B) Averiguar si un triángulo es rectángulo
62 + 72 ≠ 112 62 + 82 = 102

11. CUADRILÁTEROS
PARALELOGRAMOS
Lados paralelos dos a dos
TRAPECIOS:
Dos de sus lados,
(normalmente
NO PARALELOGRAMOS llamados bases) son paralelos.
TRAPEZOIDES:
Cuadriláteros que no
tienen lados paralelos.

12. PROPIEDADES
RECTÁNGULO: • Lados iguales dos a dos.
Paralelogramo que tiene
los cuatro ángulos rectos. • Las diagonales son iguales y
P se cortan en el punto medio
de cada una.
A
R
A • Los ángulos opuestos son iguales.
ROMBO:
L Paralelogramo que tiene • Diagonales perpendiculares que
E los cuatro lados iguales. se cortan en el punto medio
L de ambas, y son ejes de simetría.
O
G CUADRADO:
Tiene cuatro ángulos rectos, • Diagonales iguales y
R perpendiculares.
y cuatro lados iguales,
A en consecuencia es un
M • Las diagonales son
rectángulo y un rombo.
bisectrices de sus ángulos.
O
S
ROMBOIDE:
Paralelogramo que sus • Las diagonales no son iguales
ángulos no son rectos y se cortan en sus puntos
ni sus lados son iguales medios.
• Lados y ángulos iguales dos a
dos.

13. TRAPECIOS RECTÁNGULOS
Dos ángulos rectos
N TRAPECIOS
O • Los lados paralelos se
llaman bases y la distancia
entre ellos, altura.
P
A
R
A TRAPECIOS ISÓSCELES
L Los lados no paralelos iguales
E
L
O
G
R
A
M
O TRAPEZOIDES
S • Son de formas muy variadas,
la más común es en forma de COMETA

14. CLASIFICAR LOS SIGUIENTES CUADRILÁTEROS

15. PERÍMETROS Y
ÁREAS DE
FIGURAS PLANAS

16. LONGITUDES Y
ÁREAS EN LA
CIRCUNFERENCIA
Y EN EL CÍRCULO

17. CIRCUNFERENCIAS Y RECTAS: posición relativa
No tienen ningún Se cortan Se cortan
punto en común en un punto en dos puntos

18. El radio r, la mitad de la cuerda, c/2, y
la distancia del centro a la cuerda, d,
forman un triángulo rectángulo.
Por tanto , se cumple que:
2
c
r2 d2
2
Desde un punto exterior se pueden
Trazar dos tangentes a una
circunferencia. Cada una de ellas es
perpendicular al radio en el punto de
tangencia. Por tanto, el triángulo de
lados d, r y t es rectángulo.
d2 r2 t2

19. ACTIVIDADES
1. Observando la figura y sabiendo
que la cuerda AB mide 18 cm.
¿Cuál es la distancia del centro
de la circunferencia a la recta?
AB = 12 cm
2. Halla la longitud del segmento PT
PT = 36 cm

20. ÁNGULOS EN LA CIRCUNFERENCIA
ÁNGULO CENTRAL
La medida angular de un arco PQ
es el ángulo central
correspondiente POQ
PQ = POQ
ÁNGULO INSCRITO
La medida de un ángulo inscrito
en una circunferencia es igual a
la mitad del arco que abarca,
es decir, a la mitad del
ángulo central correspondiente

21. ACTIVIDADES
ˆ ˆ ˆ
1. ¿Cuánto miden los ángulos P , Q y R
si AOB es un ángulo recto?
2. El triángulo ABC es isósceles,
¿cuánto miden los ángulos de ese triángulo?

22. 3. Halla el valor de los ángulos señalados en cada figura:
“ “ “

23. ACTIVIDADES
Calcula el área de la parte coloreada en las siguientes figuras
c)
a)
AB 10 cm
CD 16 cm
AC BD 5 cm
b)
r = 2 cm
R = 5 cm

24. ELEMENTOS DE UN POLÍGONO

26. FIGURAS EN EL ESPACIO
FIGURAS POLIÉDRICAS FIGURAS DE REVOLUCIÓN
Son cuerpos geométricos Son cuerpos que se engendran al
limitados por polígonos hacer girar figuras planas alrededor
de un eje.

27. POLIEDROS
Un poliedro es la región del espacio limitada por polígonos.
ELEMENTOS DE UN POLIEDRO

28. Caras
Las caras de un poliedro son cada uno de los polígonos que limitan al poliedro.
Aristas
Las aristas de un poliedro son los lados de las caras del poliedro. Dos
caras consecutivas tienen una arista en común.
Vértices
Los vértices de un poliedro son los vértices de cada una de las caras del
poliedro. Tres caras coinciden en un mismo vértice.
Ángulos diedros
Los ángulos diedros están formados por cada dos caras y tienen una arista
en común.
Ángulos poliédricos
Los ángulos poliédricos están formados por tres o más caras del poliedro y
tienen un vértice común.
Diagonales
Las diagonales de un poliedro son los segmentos que unen dos vértices no
pertenecientes a la misma cara.

29. PRISMAS
Tienen dos caras iguales y paralelas, BASES.
Caras laterales que son paralelogramos.

30. Otros elementos importantes de los prismas
ARISTA BÁSICA
ARISTA LATERAL
ALTURA
APOTEMA BASE

31. PRISMAS
Sus caras son romboides
OBLICUOS o rombos
RECTOS
REGULARES IRREGULARES
Sus bases son Sus bases son
polígonos regulares polígonos irregulares
Sus caras laterales son rectángulos o cuadrados

32. PIRÁMIDES
Tienen una sola base.
Caras laterales son triángulos.
BASE
CARAS LATERALES

33. Otros elementos importantes de las pirámides
APOTEMA LATERAL O
ALTURA DE LA CARA
ARISTA LATERAL
ALTURA DE LA PIRÁMIDE
APOTEMA BASE
a´
ARISTA BÁSICA
BASE

34. PIRÁMIDES
Alguna de sus caras
OBLICUAS no es triángulo isósceles
RECTAS
REGULARES IRREGULARES
Su base es un Su base es un
polígono regular polígono irregular
Sus caras son triángulos isósceles

35. Pirámides rectas y oblicuas
El nombre te dice dónde está la punta (ápice) de la pirámide.
Si el ápice está directamente sobre el centro de la base, es una pirámide
recta, si no es una pirámide oblicua
Centro de la base
Pirámide Recta Pirámide Oblicua

36. ALGUNAS FIGURAS POLIÉDRICAS: ELEMENTOS

37. PARALELEPÍPEDO ORTOEDRO:
Prisma cuyas bases Paralelepípedo cuyas caras
son paralelogramos. son rectángulos
Tiene 6 caras y todas
son paralelogramos.
CUBO:
Paralelepípedo cuyas
6 caras son cuadrados

38. Clasifica los siguientes cuerpos geométricos:
¿Qué tienen en común todos estos cuerpos geométricos?

39. Poliedros Regulares
Un poliedro regular tiene todos sus ángulos diedros y todos sus
ángulos poliedros iguales y sus caras son polígonos regulares
iguales.
Sólo existen cinco poliedros regulares:
Tetraedro: cuatro caras que son triángulos equiláteros
Hexaedro o cubo: seis caras que son cuadrados
Octaedro: ocho caras que son triángulos equiláteros
Dodecaedro: doce caras que son pentágonos regulares
Icosaedro: veinte caras que son triángulos equiláteros

40. Poliedros Regulares
Icosaedro
Tetraedro Octaedro
Hexaedro
Dodecaedro

41. TEOREMA DE EULER
Siempre en un poliedro simple o convexo (poliedro que no
tiene orificios), al contar sus caras (c), sus vértices (v) y sus
aristas (a), se cumple la siguiente relación:
A=C+V–2 Fórmula de Euler
Caras = 8
Vértices = 12 8 + 12 – 2 = 18
Aristas = 18

42. DIAGONALES DE UN POLIEDRO

43. CUERPOS DE REVOLUCIÓN
ESFERA CONO
CILINDRO

44. CILINDRO
Se obtiene al girar un rectángulo alrededor
de uno de sus lados.
EJE GIRO
RADIO
generatriz
altura
GENERATRIZ
BASE
radio

45. CONO
Se obtiene al girar un triángulo rectángulo
alrededor de uno de sus catetos.
EJE GIRO
GENERATRIZ
altura
eje giro
RADIO
BASE
radio

46. ESFERA
Se obtiene al girar un semicírculo alrededor
de su diámetro.
GENERATRIZ
CENTRO
diámetro
eje giro
RADIO
EJE DE GIRO

47. ALGUNAS FIGURAS DE REVOLUCIÓN: ELEMENTOS

49. Esfera solar de Knoxville

50. Vista nocturna del monumento en recuerdo y
homenaje a las víctimas del atentado del 11-M,
erigido en las proximidades de la estación de
Atocha, en Madrid

53. A continuación tienes dibujados algunos cuerpos
a. ¿Qué características comunes ves a todos ellos?.
b. Clasifica cada uno de ellos.
c. Indica número de vértices, caras y aristas de cada uno de ellos.
d. Piensa objetos reales en los que aparezcan poliedros.

54. De las siguientes figuras indica cuáles son poliedros y cuáles cuerpos de
Revolución.
Indica también el nombre de cada uno de ellos.

55. Áreas y Volúmenes
de cuerpos en el
espacio

56. PRISMA

57. CILINDRO

58. PIRÁMIDE

59. CONO

60. ESFERA

61. ACTIVIDADES
1. Indica, razonando tu respuesta, cuáles de las siguientes
figuras son poliedros. ¿Alguno de los poliedros que hay es regular?
2. Halla el volumen y el área total de cada una de estas figuras:

62. SÓLIDOS PLATÓNICOS
Polígonos que lo forman:
V A C Nombre (Procede del...)
Tr Cu Pe Ex Oc De
12 18 8 Tetraedro truncado (T) 4 4
24 36 14 Cubo truncado (C) 8 6
24 36 14 Octaedro truncado (O) 6 8
60 90 32 Dodecaedro truncado (D) 20 12
60 90 32 Icosaedro truncado (I) 12 20
12 24 14 Cuboctaedro (C,O) 8 6
24 48 26 Rombicuboctaedro (C,O) 8 18
48 72 26 Gran rombicuboctaedro (C,O) 12 8 6
24 60 38 Cubo doblemente truncado (C) 32 6
30 60 32 Icosidodecaedro (D,I) 20 12
60 120 62 Rombicosidodecaedro (D,I) 20 30 12
120 180 62 Gran rombicosidodecaedro (D,I) 30 20 12
60 150 92 Dodecaedro doblemente truncado (D) 80 12

63. TETRAEDRO TRUNCADO CUBOTRUNCADO
OCTAEDRO TRUNCADO
ICOSAEDRO TRUNCADO DODECAEDRO TRUNCADO

64. ICOSIDODECAEDRO CUBOCTAEDRO ROMBICUBOCTAEDRO
CUBO ACHATADO DODECAEDRO ACHATADO

65. GRAN ROMBICUBOCTAEDRO
ROMBICOSIDODECAEDRO
GRAN ROMBICOSIDODECAEDRO