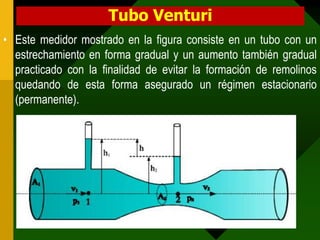
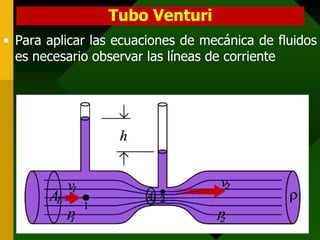
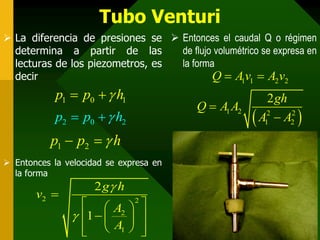
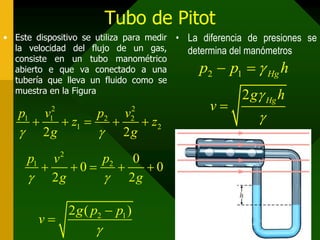
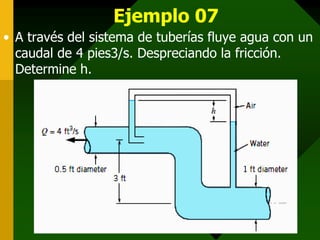
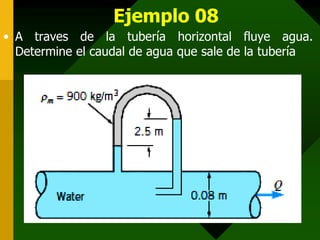
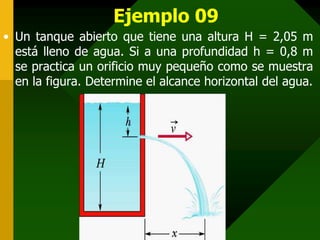
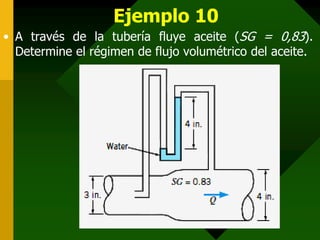
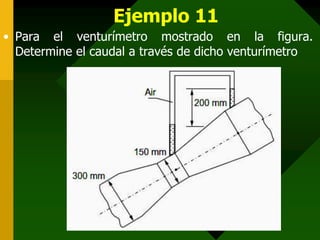
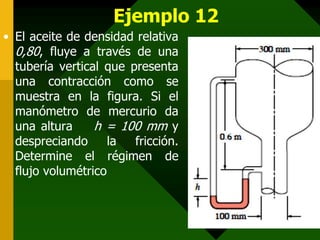
Este documento presenta conceptos fundamentales de hidrodinámica como el movimiento de fluidos, viscosidad, tipos de flujo, líneas de corriente, tubos de corriente, ecuación de continuidad, ecuación de Bernoulli, aplicaciones como la ecuación de la hidrostática, teorema de Torricelli, tubo de Venturi y tubo de Pitot, y resuelve varios ejemplos numéricos aplicando estas ecuaciones.

1. HIDRODINAMICA
PRESENTADO POR
Emma vera
Samuel Santamaría
Juan carlós Martínez
Dixon Flores
Nicol Moreno

2. Caida de agua en el
parque Nacional de
Yellowstone.
El agua en la parte
superior de la catarata
pasa por un
estrechamiento en
donde su velocidad se
incrementa.
En este Capitulo
estudiaremos el
movimiento de fluidos
Movimiento de fluidos

3. HIDRODINÁMICA
Estudia el movimientos de los fluidos, es
decir, el flujo de los fluidos

4. VISCOCIDAD
• Aparece como producto de la interacción de las moléculas
del fluido cuando éste se mueve a través de ductos en los
flujos laminares y turbulentos. Es decir la viscosidad se
debe al rozamiento interno del fluido
• La viscosidad en los líquidos disminuye con el aumento de
la temperatura mientras que en los gases sucede lo
contrario

5. Flujo de fluidos
• Llamase flujo de fluidos al movimiento de fluidos.
Pueden ser:
• (a) Permanente y no permanente
• (b) Uniforme y no uniforme
• (c) laminar o turbulunto
• (d) Real o Ideal
• (e) Rotacional e irrotacional
• (f) Viscoso y no viscoso
• (g) Compresible e incompresible

6. LINEA DE CORRIENTE
 Las líneas de corriente son líneas imaginarias dibujadas a
través de un fluido en movimiento y que indican la dirección de
éste en los diversos puntos del flujo de fluidos.
 Debe observarse que la tangente en un punto a la línea de
corriente nos da la dirección instantánea de la velocidad de las
partículas del fluido, en dicho punto.

7. TUBO DE CORRIENTE
Es la parte de un fluido limitado por un haz de líneas de corriente.
Todas las partículas que se hallan en una sección de un tubo de
corriente, al desplazarse continúan moviéndose por su sección sin
salirse del mismo. De igual forma ninguna partícula exterior al
tubo de corriente puede ingresar al interior del tubo.

8. ECUACIÓN DE CONTINUIDAD
La masa no se crea
ni se destruye. Es
decir siempre se
conserva

9. ECUACIÓN DE CONTINUIDAD
De acuerdo a la conservación de la
masa, la cantidad de masa que fluye
a través de la tubería es la misma
1 2
1 1 1 2 2 2
1 1 2 2
m
Av
t
m m
Av t A v t
Av A v
Q Av

 


  
  


Si el flujo es incompresible,
la densidad es constante
Ecuación de continuidad
A esta ecuación se llama caudal o gasto

10. Ecuación de Bernoulli
 Es una ecuación de importancia en la mecánica de los fluidos ideales (se
desprecia las fuerzas de rozamiento, el flujo debe ser estable e incompresible) y
constituye una expresión del principio de conservación de la energía. Se
considera que en el flujo existen tres tipos de energía: la energía cinética
debida al movimiento, la energía debida a la presión y la energía potencial
gravitatoria debida a la elevación. Matemáticamente se escribe
2 2
1 1 2 2
1 2
2 2
p v p v
y y
g g 
    
2
2
p v
y H Cte
g
   

11. IX. APLICACIONES DE LA ECUACION DE BERNOULLI.
1. La ecuación de la hidrostática.
Para determinar la ecuación
hidrostática se aplica la ecuación de
Bernoulli entre los puntos 1 y 2 de la
Como el depósito está abierto sobre
la superficie libre del fluido actúa la
presión atmosférica p0. Así mismo,
debido a que el fluido está en reposo,
v1 y v2 son nulas, con lo que la
ecuación anterior se escribe
2 2
1 1 2 2
1 2
2 2
p v p v
z z
g g 
    
 
01
1 2
1 0 2 1
1 0
0 0
pp
z z
p p z z
p p h
 


    
  
 

12. APLICACIONES DE LA ECUACION DE BERNOULLI.
2. Teorema de Torricelli.
 Permite determinar la velocidad de
salida de un fluido a través de una
boquilla. Se aplica la ecuación de la
continuidad
 La ecuación de Bernoulli nos da
 Debido a que las presiones en los
puntos 1 y 2 son las mismas esto es la
presión atmosférica p0, la ecuación
anterior se escribe.
2 2
1 1 2 2
1 2
2 2
p v p v
z z
g g 
    
1 1 2 2Av A v
 
2 2
0 01 2
1 2
2 2
2 1 2 1
2 2
2 1
2 2
2
2
p pv v
z z
g g
v v g z z
v v gh
 
    
  
 

13. APLICACIONES DE LA ECUACION DE BERNOULLI.
2. Teorema de Torricelli..
 De las ecuaciones anteriores se
tiene
 En general el área de la tobera A2
es mucho menor que el área de la
sección transversal del depósito A1,
de tal forma que
 Esta ecuación indica que la
velocidad de descarga es igual a
la velocidad que alcanzaría una
partícula cayendo libremente sin
fricción desde el punto 1 hasta el
punto 2. En otras palabras la
energía potencial de la superficie
libre se convierte en energía
cinética del chorro.
 
2
2 2
2
1
2 2
1 2
1 2
2
1 /
A
v gh
A
gh
v
A A
  
   
   

 
 
2 2v gh

14. Tubo Venturi
• Este medidor mostrado en la figura consiste en un tubo con un
estrechamiento en forma gradual y un aumento también gradual
practicado con la finalidad de evitar la formación de remolinos
quedando de esta forma asegurado un régimen estacionario
(permanente).

15. Tubo Venturi
• Para aplicar las ecuaciones de mecánica de fluidos
es necesario observar las líneas de corriente

16. Tubo Venturi
 Para determinar el caudal en primer
lugar se determina la velocidad de
flujo del fluido aplicando la ecuación
de continuidad entre los punto 1 y 2
 Por otro lado aplicando la ecuación de
Bernoulli entre los puntos 1 y 2 se
tiene
• Observando la figura se ve que
z1 y z2 se encuentran en un
mismo nivel horizontal por lo
que
• Combinando las ecuaciones 1 y 2
1 1 2 2
2
2 2
1
Av A v
A
v v
A


2 2
1 1 2 2
1 2
2 2
p v p v
z z
g g 
    
2 2
1 1 2 2
2 2
p v p v
g g 
  
 2 2
2 1 1 2
2g
v v p p

  
 1 2
2 2
2
1
2
1
g p p
v
A
A



  
  
   

17. Tubo Venturi
 La diferencia de presiones se
determina a partir de las
lecturas de los piezometros, es
decir
 Entonces la velocidad se expresa en
la forma
 Entonces el caudal Q o régimen
de flujo volumétrico se expresa en
la forma
1 0 1p p h 
2 0 2p p h 
1 2p p h 
2 2
2
1
2
1
g h
v
A
A



  
  
   
 
1 1 2 2
1 2 2 2
1 2
2
Q Av A v
gh
Q A A
A A
 



18. Tubo de Venturi

19. Tubo de Pitot
• Este dispositivo se utiliza para medir
la velocidad del flujo de un gas,
consiste en un tubo manométrico
abierto e que va conectado a una
tubería que lleva un fluido como se
muestra en la Figura
• La diferencia de presiones se
determina del manómetros
2 12 ( )g p p
v



2 1 Hgp p h 
2 Hgg h
v


2 2
1 1 2 2
1 2
2 2
p v p v
z z
g g 
    
2
1 2 0
0 0
2 2
p pv
g g 
    

20. Tubo de Pitot

21. EJEMPLO 01
En la figura, los diámetros interiores del conducto en las
secciones 1 y 2 son de 50 mm y 100 mm,
respectivamente. En la sección 1 fluye agua a 70°C con
velocidad promedio de 8 m/s. Determine: (a) la
velocidad en la sección 2, (b) el caudal

22. EJEMPLO 02
En la figura, los diámetros
interiores del conducto en
las secciones 1 y 2 son de
50 mm y 100 mm,
respectivamente. En la
sección 1 fluye agua a
70°C con velocidad
promedio de 8 m/s.
Determine: (a) la
velocidad en la sección 2,
(b) el caudal

23. Ejemplo 03
• Un tanque abierto grande contiene una capa de aceite
flotando sobre el agua como se muestra en la figura.
El flujo es estable y carece de viscosidad. Determine:
(a) la velocidad del agua en la salida de la boquilla (b)
la altura h a la cual se elevará el agua que sale de una
boquilla de 0,1 m de diámetro.

24. Ejemplo 04
• Fluye agua continuamente de un tanque abierto como se
muestra en la figura. La altura del punto 1 es de 10 m, y la de
los puntos 2 y 3 es de 2 m. El área transversal en el punto 2 es
de 0,03 m2, en el punto 3 es de 0,015 m2. El área del tanque es
muy grande en comparación con el área transversal del tubo.
Determine: (a) el flujo volumétrico y (b) la presión
manométrica del punto 2.

25. Ejemplo 05
• Para el sifón mostrado en la figura, calcular: (a) el
caudal de aceite que sale del tanque, y (b) las
presiones en los puntos B y C.

26. Ejemplo 06
• ¿Qué presión p1 se
requiere para obtener un
gasto de 0,09 pies3/s del
depósito que se muestra
en la figura?. Considere
que el peso específico de
la gasolina es γ = 42,5
lb/pie3.

27. Ejemplo 07
• A través del sistema de tuberías fluye agua con un
caudal de 4 pies3/s. Despreciando la fricción.
Determine h.

28. Ejemplo 08
• A traves de la tubería horizontal fluye agua.
Determine el caudal de agua que sale de la tubería

29. Ejemplo 09
• Un tanque abierto que tiene una altura H = 2,05 m
está lleno de agua. Si a una profundidad h = 0,8 m
se practica un orificio muy pequeño como se muestra
en la figura. Determine el alcance horizontal del agua.

30. Ejemplo 10
• A través de la tubería fluye aceite (SG = 0,83).
Determine el régimen de flujo volumétrico del aceite.

31. Ejemplo 11
• Para el venturímetro mostrado en la figura.
Determine el caudal a través de dicho venturímetro

32. Ejemplo 12
• El aceite de densidad relativa
0,80, fluye a través de una
tubería vertical que presenta
una contracción como se
muestra en la figura. Si el
manómetro de mercurio da
una altura h = 100 mm y
despreciando la fricción.
Determine el régimen de
flujo volumétrico