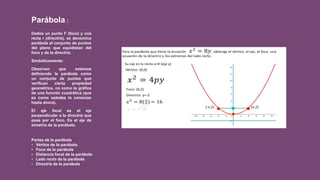
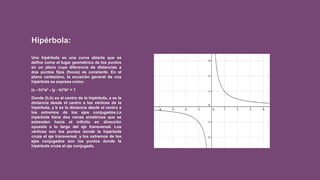
El documento presenta información sobre el plano numérico y diferentes conceptos matemáticos relacionados. Explica que el plano numérico es un sistema de coordenadas bidimensional que utiliza números para ubicar puntos, y describe elementos como el origen, coordenadas, distancia entre puntos, y ecuaciones que representan líneas y curvas. También define conceptos como circunferencias, elipses, parábolas, hipérbolas y cónicas, y sus características geométricas.

1. Republica Bolivariana De Venezuela
Ministerio Del Poder Popular Para La Educación Superior
Universidad Politécnica Territorial Andrés Eloy Blanco
Programa Nacional De Distribución Y Logística
Barquisimeto Edo Lara
PLANO
NUMÉRICO
Integrantes:
Ivor Azuaje. C.I: 28021184
Pierina Contreras. C.I: 31466927
Angely Sivira. C.I: 31926422
Luisana Rojas. C.I: 31558788
Sección: 0202
13 de diciembre del 2023

2. Plano numérico:
En matemáticas, un plano numérico es un sistema de coordenadas
bidimensional que utiliza números para ubicar puntos en un plano. En
este sistema, se utilizan dos ejes perpendiculares, uno horizontal y otro
vertical, para representar las coordenadas x e y de un punto. La
intersección de los dos ejes se conoce como el origen y se representa
por el punto (0,0). Los puntos en el plano se representan mediante pares
ordenados de números, donde el primer número representa la
coordenada x y el segundo número representa la coordenada y. Por
ejemplo, el punto (2,3) se encuentra a dos unidades a la derecha del
origen y tres unidades hacia arriba. El plano numérico es una
herramienta fundamental en muchas áreas de las matemáticas,
incluyendo la geometría, el álgebra y el cálculo.

3. Distancia:
La distancia entre dos puntos
no es más que la longitud del
segmento de la recta que los
conecta, el segmento de recta
es el pedacito de recta de un
punto a otro, puede ser de
manera horizontal, vertical u
oblicua (significa inclinada).
Para conocer la distancia entre
dos puntos se utilizará el
teorema de Pitágoras que
explica que: en todo triangulo
rectángulo el cuadrado de la
hipotenusa es igual a la suma
de los cuadrados de los
catetos.
Sean (a, b) e (x, y) dos puntos de R2, se define la
distancia de (a, b) a (x, y) como:
Es decir, la distancia es la raíz cuadrada de la
suma de los cuadrados de la diferencia de las
coordenadas de los puntos.
Ejemplo
La distancia entre los
puntos (2,2)(2,2) y (2,4)(2,4) es 22:
Representación

4. Punto Medio:
Es el punto que se
encuentra a la
misma distancia de
otros dos puntos
cualquiera o
extremos de un
segmento. Punto
medio de un
segmento, hallado
mediante regla y
compás: el punto
medio es la
intersección de la
recta roja con el
segmento en
negro.
Ejemplo
Encuentre el punto medio entre (–2, 5) y (7, 7).
Use la fórmula. Las coordenadas del punto
medio son:
Simplifique.
Representación

5. Ecuaciones en el
plano numérico:
En el plano numérico, las ecuaciones se utilizan para
representar gráficamente relaciones entre variables.
Por ejemplo, la ecuación y = 2x + 1 representa una
línea recta en el plano numérico, donde cada punto en
la línea satisface la relación entre x e y dada por la
ecuación. Para graficar la línea, se pueden encontrar
dos puntos que satisfagan la ecuación (por ejemplo,
cuando x = 0, y = 1 y cuando x = 1, y = 3) y trazar una
línea recta que los conecte. Otra forma de graficar la
línea es utilizar la pendiente-intercepto, que es la
forma y = mx + b, donde m es la pendiente de la línea y
b es el punto donde la línea cruza el eje y (también
conocido como el término constante). En este caso, la
pendiente es 2 y el punto de intersección con el eje y
es 1, por lo que se puede graficar la línea trazando una
línea recta con una pendiente de 2 que pase por el
punto (0,1). Las ecuaciones también se utilizan para
representar curvas en el plano numérico, como
círculos, elipses y parábolas.

6. Trazado de
circunferencias
Para trazar una circunferencia en el plano
numérico, se necesitan dos datos: el centro de
la circunferencia y su radio. El centro se
representa por un punto (h,k) y el radio por una
línea recta que une el centro con cualquier
punto de la circunferencia. Para dibujar la
circunferencia, se puede marcar el centro en el
plano numérico y luego trazar una línea recta
de longitud igual al radio en cualquier
dirección. A continuación, se puede girar esta
línea alrededor del centro, marcando puntos a
lo largo de ella para formar la circunferencia.
Repitiendo este proceso en diferentes
direcciones, se pueden marcar más puntos y
trazar una curva suave que los conecte para
obtener la circunferencia completa.

7. Dados un punto F (foco) y una
recta r (directriz), se denomina
parábola al conjunto de puntos
del plano que equidistan del
foco y de la directriz.
Simbólicamente:
Observen que estamos
definiendo la parábola como
un conjunto de puntos que
verifican cierta propiedad
geométrica, no como la gráfica
de una función cuadrática (que
es como ustedes la conocían
hasta ahora).
El eje focal es el eje
perpendicular a la directriz que
pasa por el foco. Es el eje de
simetría de la parábola.
Parábola :
Partes de la parábola
• Vértice de la parábola
• Foco de la parábola
• Distancia focal de la parábola
• Lado recto de la parábola
• Directriz de la parábola

8. Elipses:
La elipse es el lugar
geométrico de los puntos
del plano cuya suma de
distancias a dos puntos fijos
llamados focos es
constante.
La elipse es el lugar
geométrico de los puntos
del plano cuya suma de sus
distancias a dos puntos fijos
denominados focos es
constante.
ELEMENTOS DE LA ELIPSE
Focos
Eje focal
Eje secundario
Centro
Radio vectores
Distancia focal
Vértice
Eje mayor
Eje menor
Eje de simetría
Centro de simetría
A partir de estos
elementos, podemos
construir las relaciones
fundamentales de la elipse;
así como calcular su
excentricidad, tal como
veremos a continuación.

9. Hipérbola:
Una hipérbola es una curva abierta que se
define como el lugar geométrico de los puntos
en un plano cuya diferencia de distancias a
dos puntos fijos (focos) es constante. En el
plano cartesiano, la ecuación general de una
hipérbola se expresa como:
(x - h)²/a² - (y - k)²/b² = 1
Donde (h,k) es el centro de la hipérbola, a es la
distancia desde el centro a los vértices de la
hipérbola, y b es la distancia desde el centro a
los extremos de los ejes conjugados.La
hipérbola tiene dos ramas simétricas que se
extienden hacia el infinito en dirección
opuesta a lo largo del eje transversal. Los
vértices son los puntos donde la hipérbola
cruza el eje transversal, y los extremos de los
ejes conjugados son los puntos donde la
hipérbola cruza el eje conjugado.

10. Cónica:
Una ecuación cónica es una ecuación algebraica
que describe una curva cónica en un plano. Las
cónicas más comunes son la elipse, la parábola y
la hipérbola, y cada una de ellas tiene una forma
específica de ecuación. Estas ecuaciones se
utilizan en matemáticas, física, ingeniería y otras
áreas para modelar situaciones en las que se
producen curvas cónicas.
Una superficie cónica esta engendrada por el giro
de una recta , que llamamos generatriz, alrededor
de otra recta , eje, con el cual se corta en un punto
, vértice.
= la generatriz
= el eje
= el vértice

11. Bibliografía:
https://www.todamateria.com/plano-cartesiano/
https://todosistemaspro.com/10-ejercicios-practicos-de-ecuaciones-en-el-plano-cartesiano/
https://www.superprof.es/apuntes/escolar/matematicas/algebra/ecuaciones/ejercicios-de-sistemas-de-ecuaciones-por-
metodo-grafico.html
https://www.profesorenlinea.cl/geometria/Ecuacion_Circunferencia.html
https://aga.frba.utn.edu.ar/parabola/
(2) cs 1.6 no se inicia al haber cambiado los akins de armas,personajes,etc (solucion) - YouTube
https://www.superprof.es/diccionario/matematicas/analitica/elipses.html
uruguayeduca.anep.edu.uy/recursoseducativos/4521#:~:text=Una%20hipérbola%20es%20también%20un,%27)%
https://aga.frba.utn.edu.ar/hiperbola/20es%20constante%20(2a).