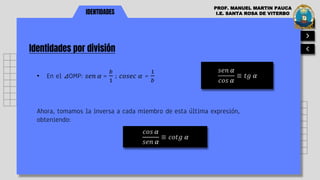
El documento presenta las identidades trigonométricas fundamentales y auxiliares. Introduce las identidades recíprocas, por división y pitagóricas. Luego explica identidades auxiliares como sen4α + cos4α = 1 - 2sen2αcos2α. Finalmente, muestra ejemplos de demostración y simplificación de identidades trigonométricas.