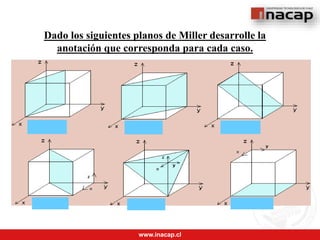
Este documento explica los índices de Miller, que se utilizan para identificar los planos cristalinos y las direcciones en una celda unitaria. Describe cómo se calculan los índices de Miller para planos y direcciones, usando sistemas de coordenadas y restas vectoriales. También cubre aspectos especiales de los índices de Miller para celdas hexagonales y ejemplos numéricos de cómo determinar índices para diferentes planos y direcciones dadas.

1. www.inacap.cl
Índices de Miller
Ciencia y Tecnología de los materiales.
Cristhopfer Castro Guerra.
Índices de Dirección

2. www.inacap.cl
Índices de Miller
• Estos se utilizan para identificar los planos cristalinos por donde es
susceptible de deslizar unos átomos sobre otros átomos en la celda
cristalina.
• Para poder identificar unívocamente un sistema de planos
cristalográficos se les asigna un juego de tres números que reciben
el nombre de índices de Miller. Los índices de un sistema de planos
se indican genéricamente con las letras (h k l)
• Los índices de Miller son números enteros, que pueden ser
negativos o positivos, y son primos entre sí. El signo negativo de un
índice de Miller debe ser colocado sobre dicho número.

3. www.inacap.cl
Ejes y celdas unitarias
A. Eje X positivo se usa saliendo
del papel.
B. Eje Y positivo hacia la
derecha y
C. Eje Z positivo hacia la parte
superior.
En sentidos opuestos se encuentran sus respectivas
zonas y cuadrantes negativos

4. www.inacap.cl
Direcciones en la celda unitaria
Procedimiento para hallar los Índices De Miller de las direcciones:
• Usar sistema de ejes coordenados completamente definidos (zonas positivas y
zonas negativas).
• Restar las coordenadas de los puntos a direccionar (cabeza menos cola),
generando el vector dirección y la cantidad de parámetros de red recorridos
• Eliminar o reducir de la resta de puntos las fracciones hasta su mínima expresión
• Encerrar los números resultantes entre corchetes , sin comas, si el resultado es
negativo en cualquier eje (X, Y, Z) debe situarse una barra o raya encima de dicho
numero, o números.
Existen direcciones y posiciones en una celda unitaria de gran interés,
dichas direcciones son los denominados Índices De Miller y son
particularmente las posiciones o lugares por donde es más susceptible un
elemento en sufrir dislocaciones y movimientos en su interior cristalino.

5. www.inacap.cl
Ejemplo de dirección en celdas cubicas
Determinar los índices de Miller de las siguientes direcciones.
Marque direcciones en la celda.
a) Punto de inicio, origen, punto
final (1,0,0)
b) Punto de inicio, origen, punto
final (1,1,1)
c) Punto de inicio, (½,-1,0) , punto
final (0,0,1)

6. www.inacap.cl
Importancia en el análisis y creación de las
direcciones en los Índices De Miller
• Las direcciones de Miller son vectores, por ende este puede ser positivo o
negativo, y con ello poseer la misma línea de acción pero diferente sentido.
• Una dirección y sus múltiplos son idénticos solo que estos aun no han sido
reducidos.
• Ciertos grupos de direcciones poseen equivalentes, esto en un sistema
cubico es ocasionado por el orden y el sentido de los vectores, ya que, es
posible redefinir el sistema coordenado para una misma combinación de
coordenadas.
Estos grupos reciben el nombre de direcciones de una forma o familia, y se
denota entre paréntesis especiales <>. Es importante resaltar que un material
posee las mismas propiedades en todas y cada una de las diferentes
direcciones de una familia.

7. www.inacap.cl
Direcciones de forma o Familia
• Dirección Planos.
<<100>> (1 0 0) (0 0 1) (0 0 1) (1 0 0) (0 1 0) (0 0 1)
6 planos
<<110>> (1 1 0) (1 0 1) (0 1 1) (1 1 0) (1 1 0) (1 0 1)
(1 1 0) (1 0 1) (0 1 1) (0 1 1) (0 1 1) (1 0 1)
12 planos
<<111>> (1 1 1) (1 1 1) (1 1 1) (1 1 1) (1 1 1) (1 1 1)
(1 1 1) (1 1 1)
08 planos

8. www.inacap.cl
Importancia de las direcciones cristalográficas
• Si son conocidas las direcciones cristalográficas, se asegura la orientación
de un solo cristal o de un material poli cristalino.
Dicha orientación nos ayudará a determinar en un material, por ejemplo en
que dirección es más fácil deformarlo.
En la dirección a lo largo de la cual los átomos están en mayor contacto.
En la industria esto es de vital importancia para el uso, deformación y
construcción de nuevos elementos y materiales.
En general es necesario encontrar o tener en cuenta la posición y dirección
cristalográfica de los elementos, ya que, así podrá aprovecharse al máximo
sus propiedades mecánicas.

9. www.inacap.cl
Planos en la celda unitaria
Los planos cristalinos son con mayor precisión los lugares por donde un
material facilita su deslizamiento y transformación física.
En los planos existe la mayor posibilidad de que el elemento sufra una
dislocación.
Los metales se deforman con mayor facilidad a lo largo de los planos en los
cuales los átomos están compactados de manera más estrecha o cercana en la
celda unitaria.
Es importante resaltar la orientación y forma en la que puede crecer el cristal,
para ello es necesario analizar las tensiones superficiales producidas en los
principales planos de una celda unitaria.
Los Índices de Miller para planos se representan equivalentemente al sistema cartesiano
(X, Y, Z) = (h, k, l)

10. www.inacap.cl
Procedimiento para identificar los planos de
importancia:
Identificar los puntos donde cruza al plano de coordenadas X,Y,Z en función de
los parámetros de red (si el plano pasa por el origen se debe trasladar el
origen del sistema de coordenadas).
Los Índices de Miller para los planos cristalinos son el inverso a los puntos de
un plano cartesiano.
Se calculan los recíprocos o inversos de los puntos o intersecciones.
Si el reciproco es N/∞, donde N es cualquier numero entero real, esto
significara en el plano que para este eje el plano quedara paralelo a él sin
tocarlo.
La cantidad obtenida siempre es menor a la unidad, caso que no ocurre en el
estudio de las direcciones de los Índices de Miller.

11. www.inacap.cl
Ejemplo de planos en celdas unitarias
• Determine los índices de Miller de los planos
Desarrollo:
Paso 1) Identificar los puntos por
donde pasa el plano.
H, k, l
Paso 2) Calcular el reciproco
Paso 3) Simplificar fracciones o
eliminar fracciones
Paso 4) Determinar valor del plano
2a

12. www.inacap.cl
Aspectos importantes para los planos en los Índices de Miller
Los planos positivos y negativos son idénticos.
• los planos y sus múltiplos no son idénticos. Esto se demuestra por
medio de la densidad planar y el factor de empaquetamiento.
• Los planos de forma o familia de planos son equivalentes. Se
representan con llaves << >>
• En los sistemas cúbicos, una dirección es perpendicular a un plano
si tiene los mismos Índices de Miller que dicho plano.

13. www.inacap.cl
Índices de Miller para celdas hexagonales
• Para este tipo de estructura se ha desarrollado un especial conjunto de índices
de Miller-Bravais, debido a la simetría de la estructura.
Se utilizan cuatro ejes, aunque es de tenerse en cuenta que el eje a3 es
redundante.
• En esta nueva estructura se tomaran los índices (h, k, i, l), se asignara un eje
respectivo (a1=h, a2=k, a3=i, c=l), el eje a3 radica su existencia en la relación h
+ k = -i

14. www.inacap.cl
Ejemplo
Determine los índices de Miller-Bravais para los planos A
Desarrollo:
Paso 1) Identificar los puntos por donde
pasa el plano.
(h k i l )
a1=a2=a3= ∞ ; c = 1
Paso 2) Calcular el reciproco
(∞ ∞ ∞1)
Reciproco (1/ ∞ 1/ ∞ 1/ ∞ 1/1)
Paso 3) Simplificar fracciones
Paso 4) Determinar valor del plano
(0 0 0 1)

15. www.inacap.cl
Desarrollo:
Paso 1) Identificar los puntos por donde
pasa el plano.
(h k i l )
a1= 1 a2= ∞ a3= -1 ; c = L
Paso 2) Calcular el reciproco L unitario
distinto de a
(1 ∞ -1 1 )
Reciproco (1/ 1 1/ ∞ 1/ -1 1/1)
Paso 3) Simplificar fracciones
Paso 4) Determinar valor del plano
(1 0 1 1)
Ejemplo

16. www.inacap.cl
Ejemplo
Determine los índices de Miller-Bravais para los planos B
Desarrollo:
Paso 1) Identificar los puntos por donde
pasa el plano.
a1=a2=1 ; a3= -1/2 ; c = 1
Paso 2) Calcular el reciproco
(1 1 -2 1)
Reciproco (1/ 1 , 1/ 1, -1/ 2, 1/1)
Paso 3) Simplificar fracciones
Paso 4) Determinar valor del plano
(1 1 2 1)
-a3=1/2

17. www.inacap.cl
Dirección en la celda hexagonal.
• Dados los siguientes puntos 0,0,1 «cabeza» y 1,0,0 «cola», Calcule
indice de Miller
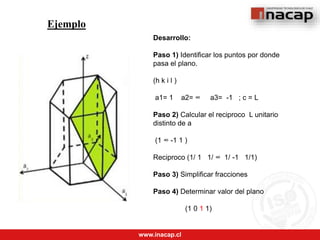
Desarrollo:
Paso 1) Identificar puntos.
Los puntos son: 0,0,1 y 1,0,0
Paso 2) Restar cabeza – cola
Cabeza - Cola: 0,0,0 – 1,0,0 = -1,-1,0
Paso 3) Eliminar fracciones y reducir enteros.
¡No existen!
Paso 4) Indicar dirección con corchete
Valorares negativos, con sombrero
[1 1 0]

18. www.inacap.cl
Dirección en la celda hexagonal.
• Dados los siguientes puntos 0,1,0 «cabeza» y 1,0,0 «cola», Calcule
indice de Miller
Desarrollo:
Paso 1) Identificar puntos.
Los puntos son: 0,1,0 y 1,0,0
Paso 2) Restar cabeza – cola
Cabeza - Cola: 0,1,0 – 1,0,0 = -1,1,0
Paso 3) Eliminar fracciones y reducir enteros.
¡No existen!
Paso 4) Indicar dirección con corchete
Valorares negativos, con sombrero
[1 1 0]

19. www.inacap.cl
Ejercicios en clases:
A. Determine los índices de las siguientes direcciones y planos
B. Dibuje las direcciones y Los planos
Obs: plano C en el origen.

20. www.inacap.cl
Dado los siguientes planos de Miller desarrolle la
anotación que corresponda para cada caso.