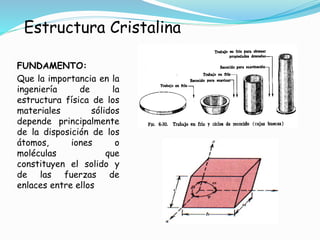
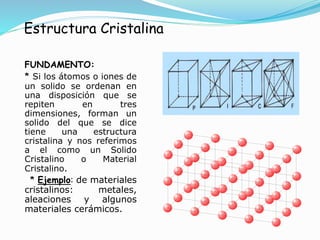
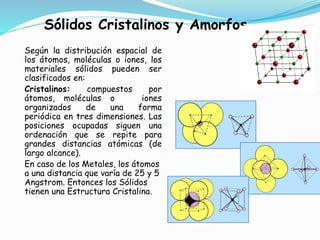
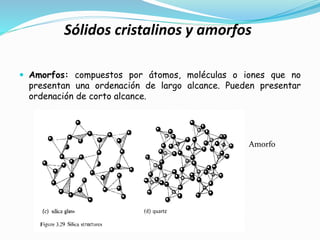
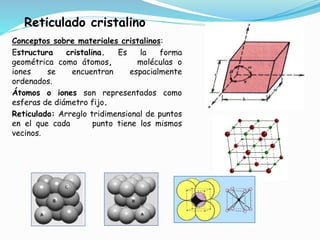
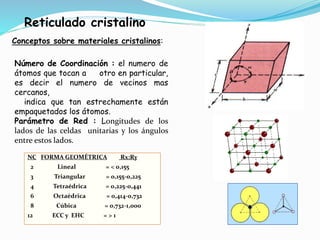
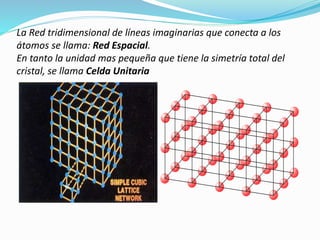
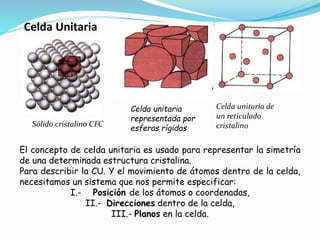
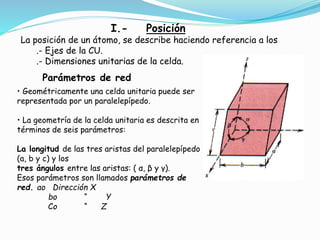
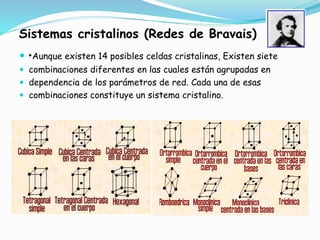
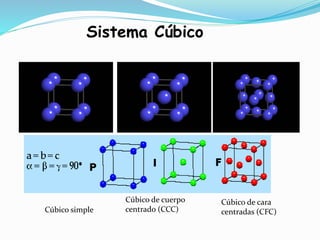
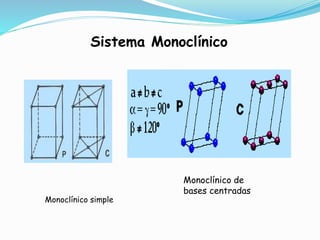
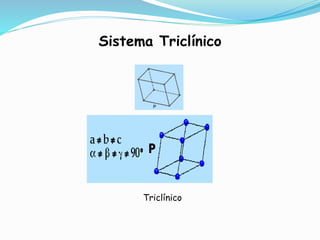
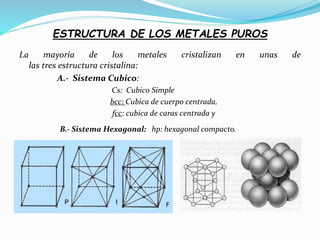
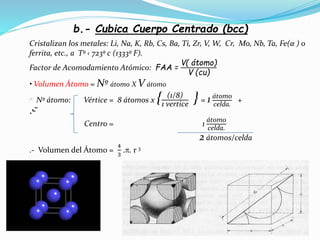
El documento describe conceptos fundamentales sobre estructuras cristalinas de materiales. Explica que los materiales sólidos pueden ser cristalinos u amorfos dependiendo del ordenamiento de los átomos que los componen. Los materiales cristalinos se caracterizan por tener una estructura cristalina donde los átomos se ordenan de forma periódica en tres dimensiones. También define conceptos como celda unitaria, sistemas cristalinos, índices de Miller y las principales estructuras cristalinas de los metales puros como cúbica simple

1. Cristalografía y
sistema CRISTALINO
cristalino
UNIVERSIDAD NACIONAL JOSE FAUSTINO
SANCHEZ CARRION
CURSO: ESTRUCTURA DE LOS METALES
Profesor: ING. Juan Manuel Ipanaqué Roña

2. Estructura Cristalina
FUNDAMENTO:
Que la importancia en la
ingeniería de la
estructura física de los
materiales sólidos
depende principalmente
de la disposición de los
átomos, iones o
moléculas que
constituyen el solido y
de las fuerzas de
enlaces entre ellos

3. Estructura Cristalina
FUNDAMENTO:
* Si los átomos o iones de
un solido se ordenan en
una disposición que se
repiten en tres
dimensiones, forman un
solido del que se dice
tiene una estructura
cristalina y nos referimos
a el como un Solido
Cristalino o Material
Cristalino.
* Ejemplo: de materiales
cristalinos: metales,
aleaciones y algunos
materiales cerámicos.

4. Estructura Cristalina
 Objetivo:
Diferenciar un material solido cristalino y un material no
cristalino.
La importancia en ingeniería de la estructura física de los
materiales.
Metales Cerámicos Polímeros Compuestos

5. Contenido
 • Definir: Sólidos Cristalinos y Amorfos
 • Describir las Diferentes Estructuras Cristalinas:
de materiales metálicos (Cfc, Ccc y Hp)
 • Sistemas Cristalinos
 • Índices de Miller: Direcciones y Planos Cristalográficos
 • Definir: Alotropía y Polimorfismo
 • Materiales mono cristalinos y poli cristalinos

6. Sólidos Cristalinos y Amorfos
Según la distribución espacial de los átomos, moléculas o
iones, los materiales sólidos pueden ser clasificados en:
 Cristalinos: compuestos por átomos, moléculas o iones
organizados de una forma periódica en tres dimensiones. Las
posiciones ocupadas siguen una ordenación que se repite para
grandes distancias atómicas (de largo alcance).
 En caso de los Metales, los átomos a una distancia que varía de
25 y 5 Angstrom. Entonces los Sólidos tienen una Estructura
Cristalina.
 Amorfos: compuestos por átomos, moléculas o iones que no
presentan una ordenación de largo alcance. Pueden presentar
ordenación de corto alcance.

7. Sólidos Cristalinos y Amorfos
Según la distribución espacial de
los átomos, moléculas o iones, los
materiales sólidos pueden ser
clasificados en:
Cristalinos: compuestos por
átomos, moléculas o iones
organizados de una forma
periódica en tres dimensiones. Las
posiciones ocupadas siguen una
ordenación que se repite para
grandes distancias atómicas (de
largo alcance).
En caso de los Metales, los átomos
a una distancia que varía de 25 y 5
Angstrom. Entonces los Sólidos
tienen una Estructura Cristalina.

8. Sólidos cristalinos y amorfos
Amorfo
 Amorfos: compuestos por átomos, moléculas o iones que no
presentan una ordenación de largo alcance. Pueden presentar
ordenación de corto alcance.

9. Reticulado cristalino
Conceptos sobre materiales cristalinos:
Estructura cristalina. Es la forma
geométrica como átomos, moléculas o
iones se encuentran espacialmente
ordenados.
Átomos o iones son representados como
esferas de diámetro fijo.
Reticulado: Arreglo tridimensional de puntos
en el que cada punto tiene los mismos
vecinos.

10. Reticulado cristalino
Conceptos sobre materiales cristalinos:
Número de Coordinación : el numero de
átomos que tocan a otro en particular,
es decir el numero de vecinos mas
cercanos,
indica que tan estrechamente están
empaquetados los átomos.
Parámetro de Red : Longitudes de los
lados de las celdas unitarias y los ángulos
entre estos lados.
NC FORMA GEOMÉTRICA Rx:Ry
2 Lineal = < 0,155
3 Triangular = 0,155-0,225
4 Tetraédrica = 0,225-0,441
6 Octaédrica = 0,414-0,732
8 Cúbica = 0,732-1,000
12 ECC y EHC = > 1

11. DEFINICIÓN:
Estructura cristalina
Es la ordenación espacial de los átomos, perfectamente
prefijada formando una Red Regular.

12. La Red tridimensional de líneas imaginarias que conecta a los
átomos se llama: Red Espacial.
En tanto la unidad mas pequeña que tiene la simetría total del
cristal, se llama Celda Unitaria

14. Celda Unitaria
Sólido cristalino CFC
Celda unitaria
representada por
esferas rígidas
Celda unitaria de
un reticulado
cristalino
El concepto de celda unitaria es usado para representar la simetría
de una determinada estructura cristalina.
Para describir la CU. Y el movimiento de átomos dentro de la celda,
necesitamos un sistema que nos permite especificar:
I.- Posición de los átomos o coordenadas,
II.- Direcciones dentro de la celda,
III.- Planos en la celda.

15. Parámetros de red
• Geométricamente una celda unitaria puede ser
representada por un paralelepípedo.
• La geometría de la celda unitaria es descrita en
términos de seis parámetros:
La longitud de las tres aristas del paralelepípedo
(a, b y c) y los
tres ángulos entre las aristas: ( α, β y γ).
Esos parámetros son llamados parámetros de
red. ao Dirección X
bo “ Y
Co “ Z
I.- Posición
La posición de un átomo, se describe haciendo referencia a los
.- Ejes de la CU.
.- Dimensiones unitarias de la celda.

16. Sistemas cristalinos (Redes de Bravais)
 •Aunque existen 14 posibles celdas cristalinas, Existen siete
 combinaciones diferentes en las cuales están agrupadas en
 dependencia de los parámetros de red. Cada una de esas
 combinaciones constituye un sistema cristalino.

17. Sistema Cúbico
Cúbico simple
Cúbico de cuerpo
centrado (CCC)
Cúbico de cara
centradas (CFC)

18. Sistema Hexagonal
Hexagonal Simple: H
Hexagonal Compacto: Hc
a = b ≠ c
α = β = 90º y γ = 120º

19. Sistema Tetragonal
Tetragonal simple
Tetragonal de
cuerpo centrado

20. Sistema Rombohédrico
a = b = c: α = β = γ ≠ 90 º
Rombohédrico (R)

21. a ≠ b ≠ c y α = β = γ = 90°
Sistema Ortorrómbico
cara
centradascuerpo centradoO simple bases centradas

22. Sistema Monoclínico
Monoclínico simple
Monoclínico de
bases centradas

23. Sistema Triclínico
Triclínico

24. ESTRUCTURA DE LOS METALES PUROS
La mayoría de los metales cristalizan en unas de
las tres estructura cristalina:
A.- Sistema Cubico:
Cs: Cubico Simple
bcc: Cubica de cuerpo centrada,
fcc: cubica de caras centrada y
B.- Sistema Hexagonal: hp: hexagonal compacto.

25. a.- Estructura Cubica Simple: Cs
Factor de Acomodamiento Atómico:
FAA =
V( átomo)
V (cu)
• Volumen Átomo = Nº átomo x V átomo
Nº átomo = 8 átomos x { (1/8)
1 vertice
} = 1 átomo
celda.
Volumen del Átomo = Volumen del Átomo =
4
3
.. r 3
• Volumen Celda unidad : a3 = (2r)3 = 8r3
FAA =
V (átomo
V (cu)
) =
Nº átomo x V átomo
V(cu)
=
1 . 𝟒
𝟑
. π . r 3
8r3 = 0.5236 = 52,36% espacio ocupado.
Es una característica de los metales puros. Ejemplo: Mn, Ge, P. etc.
Factor de Acomodamiento Atómico:
FAA =
V( átomo)
V (cu)
• Volumen Átomo = Nº átomo x V átomo
Nº átomo = 8 átomos x { (1/8)
1 vertice
} = 1 átomo
celda.
Volumen del Átomo = Volumen del Átomo =
4
3
.. r 3
• Volumen Celda unidad : a3 = (2r)3 = 8r3
FAA =
V (átomo
V (cu)
) =
Nº átomo x V átomo
V(cu)
=
1 . 𝟒
𝟑
. π . r 3
8r3 = 0.5236 = 52,36% espacio ocupado.
Es una característica de los metales puros. Ejemplo: Mn, Ge, P. etc.

26. b.- Cubica Cuerpo Centrado (bcc)
.-.-
Cristalizan los metales: Li, Na, K, Rb, Cs, Ba, Ti, Zr, V, W, Cr, Mo, Nb, Ta, Fe(α ) o
ferrita, etc., a Tº ‹ 723º c (1333º F).
Factor de Acomodamiento Atómico: FAA =
V( átomo)
V (cu)
• Volumen Átomo = Nº átomo X V átomo
.- Nº átomo: Vértice = 8 átomos x { (1/8)
1 vertice
} = 1 átomo
celda.
+
Centro = 1
átomo
celda.
2 átomos/celda
.- Volumen del Átomo =
4
3
.. r 3

27. Cubica Cuerpo Centrado (bcc)
• Volumen Celda unidad: a3 = (
4𝑟
3
) ³
* FAA =
V (átomo
V (cu)
) =
Nº átomo x V átomo
V(cu)
=
(2 . 𝟒
𝟑
. π . r 3 )
(4𝑟
3
)³ = 0.68 = 68% Vol. espacio ocupado

28. NUMERO DE COORDINACION (Nc) de bcc
Es el número de átomos vecinos equidistantes a cualquier átomo en la
red.
Cuanto mayor es el Nc, tanto mas compacto, es decir, mas densamente
empaquetado esta la red.
En bcc: cada átomo tiene 8 vecinos próximos, por lo tanto el Nc = 8

29. c. Estructura de Caras Centradas: fcc
Cristalizan: Pt, Ni, Cu, Ag, Au, Pb, Al, Ca, Fe(γ).
a).- Los átomos están localizados en:
vértice = 8 átomos x {
(1/8)
1 vertice
} = 1
átomo
celda.
+
Caras = 6 caras x (
1/2 átomo
1cara /)  3 átomo
4 átomos

30. Estructura de Caras Centradas: fcc
b).- Relación Entre Parámetro de Red y Radio Atómico: ¿a?
a .  4r a 
4r
2
.- Volumen del Átomo =
4
3
.. r 3
* Remplazando: FAA =
V (átomo
V (cu)
) =
Nº átomo x V átomo
V(cu)
=
4 . 𝟒
𝟑
π r 3
(4𝑟
2
)³ = 0.74 vol.
74% Celda ocupada es el mas compacta.

31. Numero de Coordinación del f.c.c
Nc = 12 :
.- Vértice: 4 átomos vecinos
.- Caras: 4 átomos vecinos
.- Otra celdilla: 4 átomos vecinos,
equidistan a este último pero pertenecen
a la celdilla siguiente.

32. B. Sistema Hexagonal:
Estructura Cristalina Hexagonal Compacta
En la CU de Hexagonal Simple los metales no cristalizan debido FAA es
muy bajo. Cristalizan : Ti, Mg, Zn, Be, Co, Zr, Cd.
Estructura Hp. Compacta se caracteriza, 2 planos basales, en forma de
hexágono regulares, átomos en el vértice (6) y centro de cada plano.
Además, 3 átomo capa bajo en forma de triangulo a la mitad de las
distancias entre los dos planos basales.
6 átomo propio plano
3 átomo capa superior.
NC = 12

33. Estructura Cristalina Hexagonal Compacta
FAA =
V (átomo
V (cu)
) =
Nº átomo x V átomo
V(cu)
.- Nº átomo = 3 at. centro + 2 at. plano basal(
1/2 at
1plano
)+ 12 vert (
1/6 at
1 vert
)= 6 atom
.- Volumen del Átomo =
4
3
.. r 3 y .- Volumen Celda Unidad = B x h …(ᾳ)
Donde: B =
3 a2
2
x 3 = 6r2 . 3 y
h
a
= 1,68
donde: h = 1,68 x a = 1,68 x 2r = 3,66 r
Remplazando (ᾳ) : Vcu = B.h = 6r2. 3 x (3,66 r) = 33,8 r3
FAA =
( 6 átomo x 𝟒
𝟑
.. r 3 )
33,8 r3 = 0,74vol Celda ocupada es el mas compacto.

34. Numero de Coordinación del Hc
Hp. Compacta se caracteriza:
El átomo del plano basal superior
esta rodeado:
 En el mismo planos basales= 6
átomos,
 Además, 3 átomo en capa bajo en
forma de triangulo,
 Otra celda superior, 3 átomo en
forma de triangulo
 Nc = 12

35. Índices de Miller
Notación empleada para localizar: Direcciones y
Planos en una Celda Unitaria Cubica y Hexagonal
Coordenadas Celda Unitaria : se pueden localizar puntos en una
celda estableciendo un sistema de coordenadas, con un eje 0,0,0
que sirva de referencia. Un punto cualquiera se designa (x,y,z).

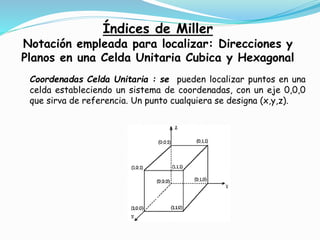
36. Índices de Miller:
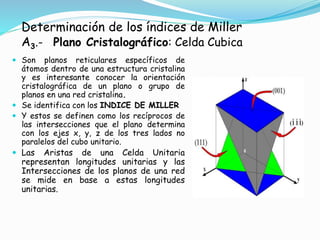
II.- Direcciones Cristalográficas
Dirección cristalográfica: vector que une dos puntos de la red
cristalina.
Procedimiento para determinación de los índices de Miller de una
Dirección Cristalográfica:
 Trasladar el “vector dirección” de manera que pase por el
origen del sistema de coordenadas.
 Determinar la proyección del vector en cada uno de los tres
ejes coordenados. Esas proyecciones deben ser medidas en
términos de los parámetros de red (a,b,c)
 Multiplicar o dividir esos tres números por un factor común,
de tal forma tal que los tres números resultantes sean los
menores enteros posibles.
 Representar la dirección escribiendo los tres números entre
corchetes: [u v w].

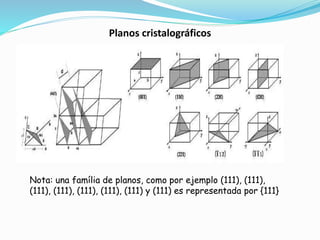
37. Direcciones Cristalográficas de un CUBO: Ejemplo
Nota: una familia de direcciones, por ejemplo [100], [100],
[010], [010], [001] y [001] es representada por <100>
X Y Z
Proyecciones en
Termino a. b y c
½ x a 1 x b 0 x c
Proyecciones 1/2 1 0
Reducción a
Mínimos Enteros
1 2 0
Notación [120]

38. Determinación de los índices de Miller
III.- Plano Cristalográfico:
 Es necesario referirnos a planos reticulares
específicos de átomos dentro de una estructura
cristalina o puede ser interesante conocer la
orientación cristalográfica de un plano o grupo de
planos en una red cristalina.
 Para identificar planos cristalográficos en una
estructura cristalina cubica se usa la notación de
INDICE DE MILLER

39. Determinación de los índices de Miller
A3.- Plano Cristalográfico: Celda Cubica
 Son planos reticulares específicos de
átomos dentro de una estructura cristalina
y es interesante conocer la orientación
cristalográfica de un plano o grupo de
planos en una red cristalina.
 Se identifica con los INDICE DE MILLER
 Y estos se definen como los recíprocos de
las intersecciones que el plano determina
con los ejes x, y, z de los tres lados no
paralelos del cubo unitario.
 Las Aristas de una Celda Unitaria
representan longitudes unitarias y las
Intersecciones de los planos de una red
se mide en base a estas longitudes
unitarias.

40. Determinación de los Índices de Miller
A3.- Plano Cristalográfico: Celda Cubica
Procedimiento para determinar Índice de Miller de un Plano en un
Cristal Cubico:
 Determinar las intersecciones del plano con los ejes del sistema de
coordenadas en términos de los parámetros: de red a, b y c.
Si el plano pasa por el origen, se debe trasladar el plano a una nueva
posición en el sistema de coordenadas.
 Obtener los recíprocos de estas tres intersecciones. Si el plano es paralelo
a uno de los ejes, la intersección se considera en el infinito y su recíproco
será cero.
 Despejar las fracciones y determinar el conjunto mas pequeño de números
enteros y estos números enteros
 Representar los índices de Miller en la forma ( h k l )
 Nota: A veces es necesario multiplicar o dividir esos tres recíprocos por un
factor común, tal que los tres números resultantes sean los menores
enteros posibles.

41. Planos cristalográficos
Nota: una família de planos, como por ejemplo (111), (111),
(111), (111), (111), (111), (111) y (111) es representada por {111}

42. B3.- Índices de Miller: Plano de celda Hcp.
Los planos en esta celda se identifican con cuatro
índices en vez de tres, llamados índices Miller-
Bravais, y
Representados por las letras h, k, i, l encerrados
entre paréntesis (h, k, i, l).
Estos índices hexagonales están basados en un
sistema coordenado de cuatro ejes:
3 ejes básicos a1, a2, a3 que forman ángulos
de120° entre sí, el cuarto eje o eje c es el eje
vertical y está localizado en el centro de la
celdilla unidad.
Los índices de esta celda se obtienen de igual
forma que para las celdas cúbicas.
Donde los recíprocos de las intersecciones que un
plano determina con los ejes a1, a2, a3
proporcionan los índices h, k e i mientras que el
reciproco de la intersección con el eje c da el índice l.

43. Espaciado Interplanar
 En ocasiones es útil
conocer la distancia
interplanar de una
misma familia de planos,
Esta distancia se halla así:
Estructuras cúbicas:
 d = a

44. Sistema de Deslizamiento
 Un sistema de deslizamiento es la combinación de un plano y una
dirección que se halla sobre el plano a lo largo del cual se produce
el deslizamiento.
 El Mecanismo de deslizamiento puede definirse como el
movimiento paralelo de dos regiones cristalinas adyacentes, una
respecto a la otra, a través de algún plano (o planos).
 Los cristales FCC poseen 12 sistemas de deslizamiento debido a
que tienen cuatro grupos {111} y con tres direcciones <110> en
cada una.

45. Observaciones generales de gran importancia en
sistemas de deslizamiento:
1.Las direcciones de deslizamiento se presentan siempre en la
dirección de empaquetamiento compacto. Existen
excepciones, por ejemplo, mercurio sólido.
2.El deslizamiento ocurre usualmente sobre la mayoría de los
planos compactos. Esta observación esta relacionada con el
hecho de que los planos empaquetados más densamente
también son el grupo de planos (hkl) ocupados, que tienen el
espaciamiento más amplio.
3.El deslizamiento se produce primero sobre el sistema de
deslizamiento que tiene el mayor esfuerzo de corte a lo largo
de su dirección de deslizamiento.

46. Alotropía o polimorfismo
 Alotropía: fenómeno en el cual un sólido (metálico o no metálico) puede
presentar más de una estructura cristalina, dependiendo de la temperatura
y de la presión (por ejemplo, Al2O3 como alúmina -α y alúmina -γ).
· Ejemplos:
 · Superconductor 123: YBa2Cu3O7-x
 · Carbono: el diamante y el grafito son constituidos por átomos de carbono
organizados en diferentes estructuras cristalinas.
GRAFITO
· Negro
· Blando
· Excelente lubricante
DIAMANTE
· Transparente
· Tenaz
. Duros Diamante Grafito

47. .
Isotropía vs. Anisotropía
i) Materiales isótropos: policristales orientados
aleatoriamente: propiedades físicas similares en todas
las direcciones.
ii) Materiales anisótropos: orientación no aleatoria de los
ejes cristalográficos: propiedades físicas pueden variar
en función de la dirección en el material.

48. Materiales Monocristalinos y Policristalinos
 Monocristalinos: presentan la
misma estructura cristalina en toda
la extensión del material sin
interrupciones. Algunos materiales
pueden existir como
monocristales grandes
(macroscópicos)
 Policristalinos: constituidos de
varios cristales o granos.
 Los límites de grano son regiones
que separan cristales de diferentes
orientaciones en un material
policristalino.
Material policristalino

49. FIN