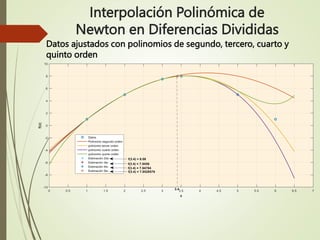
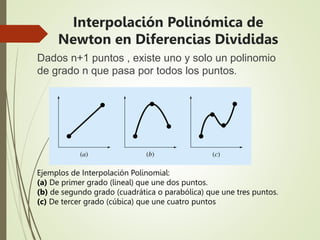
Este documento describe el método de interpolación polinómica de Newton en diferencias divididas. Explica que dado un conjunto de puntos (x, f(x)), existe un único polinomio de grado n que pasa por todos los puntos. Luego detalla cómo calcular los coeficientes del polinomio de interpolación usando diferencias divididas finitas de los valores de la función en los puntos de datos. Finalmente, muestra un ejemplo numérico donde se aplica el método para diferentes grados de polinomios e interpolar un valor intermedio.

1. INTERPOLACIÓN POLINÓMICA
DE NEWTON EN DIFERENCIAS DIVIDIDAS

2. Interpolación Polinómica de
Newton en Diferencias Divididas
Con frecuencia se encontrará que se tiene que estimar
valores intermedios entre datos definidos por puntos.
El método más común es la Interpolación Polinomial
de Newton en Diferencia Divididas. Para un
polinomio de n-enésimo grado
𝑓 𝑥 = 𝑎0 + 𝑎1𝑥 + 𝑎2𝑥2
+ ⋯ 𝑎𝑛𝑥𝑛
(ec. 1)

3. Dados n+1 puntos , existe uno y solo un polinomio
de grado n que pasa por todos los puntos.
Ejemplos de Interpolación Polinomial:
(a) De primer grado (lineal) que une dos puntos.
(b) de segundo grado (cuadrática o parabólica) que une tres puntos.
(c) De tercer grado (cúbica) que une cuatro puntos
Interpolación Polinómica de
Newton en Diferencias Divididas

4.  Interpolación Lineal: forma más simple de interpolación que
consiste en unir dos puntos es mediante una línea recta.
La notación 𝒇𝟏 𝒙 designa que este es un polinomio de
interpolación de primer grado.
Representa la pendiente de la línea que une los puntos. Es
una aproximación en diferencia dividida finita a la primera
derivada
𝑓1 𝑥 − 𝑓 𝑥0
𝑥 − 𝑥0
=
𝑓 𝑥1 − 𝑓 𝑥0
𝑥1 − 𝑥0
𝑓1 𝑥 = 𝑓 𝑥0 +
𝑓 𝑥1 − 𝑓 𝑥0
𝑥1 − 𝑥0
𝑥 − 𝑥0 ec.2
Interpolación Polinómica de
Newton en Diferencias Divididas

5.  Interpolación Cuadrática: Si se tienen tres puntos como datos, estos
pueden ajustarse en un polinomio de segundo grado. La forma
general queda expresada:
 𝑓2 𝑥 = 𝑏0 + 𝑏1 𝑥 − 𝑥0 + 𝑏2 𝑥 − 𝑥0 𝑥 − 𝑥1 ec.3
 Esta ecuación es similar a la primera
 𝑓2 𝑥 = 𝑏0 + 𝑏1𝑥 − 𝑏1𝑥0 + 𝑏2𝑥2 + 𝑏2𝑥0𝑥1 − 𝑏2𝑥𝑥0 − 𝑏2𝑥𝑥1
 Agrupando términos:
 𝑓2 𝑥 = 𝑎0 + 𝑎1𝑥 + 𝑎2𝑥2
 Donde
 𝑎0 = 𝑏0 − 𝑏1𝑥0 + 𝑏2𝑥0𝑥1
 𝑎1 = 𝑏1 − 𝑏2𝑥0 − 𝑏2𝑥1
 𝑎2 = 𝑏2
Interpolación Polinómica de
Newton en Diferencias Divididas

6.  Interpolación Cuadrática:
Para encontrar los valores de los coeficientes se evalúa en la
ecuación (3) en su orden 𝑥 = 𝑥0, 𝑥 = 𝑥1, 𝑥 = 𝑥2 para obtener:
 𝑏0 = 𝑓 𝑥0
 𝑏1 =
𝑓 𝑥1 −𝑓 𝑥0
𝑥1−𝑥0
𝑏2 =
𝑓 𝑥2 −𝑓 𝑥1
𝑥2−𝑥1
−
𝑓 𝑥1 −𝑓 𝑥0
𝑥1−𝑥0
𝑥2−𝑥0
ec.5
ec.6
ec.4
Interpolación Polinómica de
Newton en Diferencias Divididas

7.  Forma general de los polinomios de interpolación de Newton:
Se puede generalizar para ajustar a un polinomio de n-enésimo grado a
n+1 datos:
𝑓𝑛 𝑥 = 𝑏0 + 𝑏1 𝑥 − 𝑥0 + ⋯ 𝑏𝑛 𝑥 − 𝑥0 𝑥 − 𝑥1 … 𝑥 − 𝑥𝑛−1
Para un polinomio de n-enésimo grado se requieren n + 1 puntos.
Los coeficientes resultantes serán:
 𝑏0 = 𝑓 𝑥0 .
 𝑏1 = 𝑓 𝑥1, 𝑥0
 𝑏2 = 𝑓 𝑥2, 𝑥1, 𝑥0 .
 𝑏𝑛 = 𝑓 𝑥𝑛, 𝑥𝑛−1, … . , 𝑥1, 𝑥0
ec.7
ec.8
ec.9
ec.10
ec.11
Interpolación Polinómica de
Newton en Diferencias Divididas

8.  Forma general de los polinomios de interpolación de Newton:
Donde la evaluaciones de la función colocadas entre paréntesis son
diferencias divididas finitas. La primera diferencia dividida finita se
representa por:
 𝑓 𝑥𝑖, 𝑥𝑗 =
𝑓 𝑥𝑖 −𝑓 𝑥𝑗
𝑥𝑖−𝑥𝑗
La segunda diferencia dividida finita , que representa la diferencia de
las dos primeras diferencias divididas, se expresa
 𝑓 𝑥𝑖, 𝑥𝑗, 𝑥𝑘 =
𝑓 𝑥𝑖,𝑥𝑗 −𝑓 𝑥𝑗,𝑥𝑘
𝑥𝑖−𝑥𝑘
ec.12
ec.13
Interpolación Polinómica de
Newton en Diferencias Divididas

9.  Forma general de los polinomios de interpolación de Newton:
En forma similar, la enésima diferencia dividida es
 𝑓 𝑥𝑛, 𝑥𝑛−1 … . , 𝑥1, 𝑥0 =
𝑓 𝑥𝑛,𝑥𝑛−1….,𝑥1 −𝑓 𝑥𝑛−1….,𝑥1,𝑥0
𝑥𝑛−𝑥0
Estas diferencias sirven para evaluar los coeficientes en las ecuaciones
(ec.8) a (ec.11), los cuales se sustituirán en la ecuación (ec.7) para obtener
el polinomio de interpolación de Newton en diferencias divididas
 𝑓𝑛 𝑥 = 𝑓 𝑥0 + 𝑥 − 𝑥0 𝑓 𝑥1, 𝑥0 + 𝑥 − 𝑥0 𝑥 − 𝑥1 𝑓 𝑥2, 𝑥1, 𝑥0
 + … + 𝑥 − 𝑥0 𝑥 − 𝑥1 … 𝑥 − 𝑥𝑛−1 𝑓 𝑥𝑛, 𝑥𝑛−1 … . , 𝑥0
Representación gráfica de la naturaleza recursiva de las diferencias
divididas finitas.
ec.14
ec.15
Interpolación Polinómica de
Newton en Diferencias Divididas

10. Problema
 1_ Dado los datos:
x 1 2 3 3.5 5 6
f(x) 1 5 7.5 8 5 1
Calcule f(3.4) mediante polinomio de interpolación de Newton de orden 2 a 4. Escoja
la secuencia de puntos para su estimación con el fin de obtener la mejor exactitud
posible.
Construya en papel milimetrado la gráfica correspondiente a los datos y la curva de
cada polinomio obtenido. Emplee colores diferentes para cada una.
i x f(x) Primero Segundo tercero cuarto
0 1 1
1 2 5
2 3 7.5
3 3.5 8
4 5 5
5 6 1
𝟒
𝑏1 = 𝑓 𝑥1 , 𝑥0 =
𝑓 𝑥1 − 𝑓 𝑥0
𝑥1 − 𝑥0
𝑏1 = 𝑓 𝑥2 , 𝑥1 =
𝑓 𝑥2 − 𝑓 𝑥1
𝑥2 − 𝑥1
2. 𝟓
𝑏1 = 𝑓 𝑥3 , 𝑥2 =
𝑓 𝑥3 − 𝑓 𝑥2
𝑥3 − 𝑥2
𝟏. 𝟎
𝑏1 = 𝑓 𝑥4 , 𝑥3 =
𝑓 𝑥4 − 𝑓 𝑥3
𝑥4 − 𝑥3
−𝟐
𝑏1 = 𝑓 𝑥5 , 𝑥4 =
𝑓 𝑥5 − 𝑓 𝑥4
𝑥5 − 𝑥4
−𝟒
𝑏2 = 𝑓 𝑥2, 𝑥1, 𝑥0 =
𝑓 𝑥2 − 𝑓 𝑥1
𝑥2 − 𝑥1
−
𝑓 𝑥1 − 𝑓 𝑥0
𝑥1 − 𝑥0
𝑥2 − 𝑥0
−𝟎. 𝟕𝟓
𝑏2 = 𝑓 𝑥3, 𝑥2, 𝑥1 =
𝑓 𝑥3 − 𝑓 𝑥2
𝑥3 − 𝑥2
−
𝑓 𝑥2 − 𝑓 𝑥1
𝑥2 − 𝑥1
𝑥3 − 𝑥3
−𝟏
𝑏2 = 𝑓 𝑥4, 𝑥3, 𝑥2 =
𝑓 𝑥4 − 𝑓 𝑥3
𝑥4 − 𝑥3
−
𝑓 𝑥3 − 𝑓 𝑥2
𝑥3 − 𝑥2
𝑥4 − 𝑥2
−𝟏. 𝟓
𝑏2 = 𝑓 𝑥5, 𝑥4, 𝑥3 =
𝑓 𝑥5 − 𝑓 𝑥4
𝑥5 − 𝑥4
−
𝑓 𝑥4 − 𝑓 𝑥3
𝑥4 − 𝑥3
𝑥5 − 𝑥3
−𝟎. 𝟖
𝑏3 = 𝑓 𝑥3, 𝑥2, 𝑥1, 𝑥0
−𝟎. 𝟏
𝑏3 = 𝑓 𝑥4, 𝑥3, 𝑥2, 𝑥1
−𝟎. 𝟏𝟔𝟔𝟔𝟔𝟕
𝑏3 = 𝑓 𝑥5, 𝑥4, 𝑥3, 𝑥2
𝟎. 𝟐𝟑𝟑𝟑𝟑𝟑
𝑏4 = 𝑓 𝑥5, 𝑥4, 𝑥3, 𝑥2, 𝑥1, 𝑥0
−𝟎. 𝟎𝟏𝟔𝟔𝟔𝟔𝟔

11. Continuación del problema
Polinomios generados de :
Segundo orden:
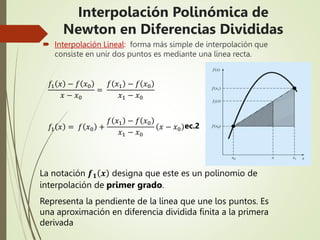
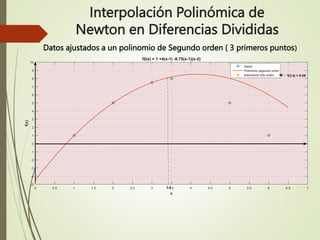
f2(x) = f(x0) +f[x1x0](x-x0) + f[x2x1x0](x-x0)(x-x1)
f2(3.4) = 1 + 4(3.4 - 1) - 0.75(3.4 - 1)(3.4 - 2) = 8.08
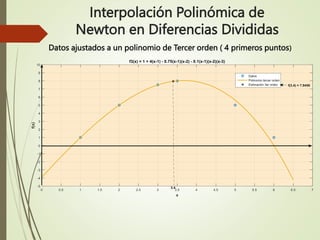
Tercer orden:
f3(x) = f(x0) +f[x1x0](x-x0) + f[x2x1x0](x-x0)(x-x1) + f[x3x2x1x0](x-x0)(x-x1)(x-x2)
f3(3.4) = 1 + 4(3.4 - 1) - 0.75(3.4 - 1)(3.4 - 2) - 0.1(3.4 - 1)(3.4 – 2)(3.4 - 3) = 7.9456
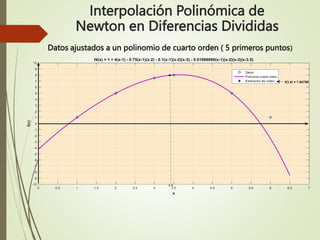
Cuarto orden:
f4(x) = f(x0) +f[x1x0](x-x0) + f[x2x1x0](x-x0)(x-x1) + f[x3x2x1x0](x-x0)(x-x1)(x-x2)
+ f[x4x3x2x1x0](x-x0)(x-x1)(x-x2)(x-x3)
f4(3.4) = 1 + 4(3.4 - 1) - 0.75(3.4 - 1)(3.4 - 2) - 0.1(3.4 - 1)(3.4 – 2)(3.4 - 3)
- 0.01666666(3.4 - 1)(3.4 – 2)(3.4 - 3)(3.4 - 3.5) = 7.94784
Quinto orden:
f5(x) = f(x0) +f[x1x0](x-x0) + f[x2x1x0](x-x0)(x-x1) + f[x3x2x1x0](x-x0)(x-x1)(x-x2)
+ f[x4x3x2x1x0](x-x0)(x-x1)(x-x2)(x-x3) + f[x5x4x3x2x1x0](x-x0)(x-x1)(x-x2)(x-x3)(x-x4)
f5(3.4) = 1 + 4(3.4 - 1) - 0.75(3.4 - 1)(3.4 - 2) - 0.1(3.4 - 1)(3.4 – 2)(3.4 - 3)
- 0.0166666(3.4 - 1)(3.4 – 2)(3.4 - 3)(3.4 - 3.5) + 0.02333333(3.4 - 1)(3.4 – 2)(3.4 - 3)(3.4 - 3.5)(3.4 - 5)
= 7.9528576

12. Datos ajustados con polinomios de segundo, tercero, cuarto y
quinto orden
Interpolación Polinómica de
Newton en Diferencias Divididas

13. Datos ajustados a un polinomio de Segundo orden ( 3 primeros puntos)
Interpolación Polinómica de
Newton en Diferencias Divididas

14. Interpolación Polinómica de
Newton en Diferencias Divididas
Datos ajustados a un polinomio de Tercer orden ( 4 primeros puntos)

15. Interpolación Polinómica de
Newton en Diferencias Divididas
Datos ajustados a un polinomio de cuarto orden ( 5 primeros puntos)