Este documento presenta el trabajo de una unidad sobre métodos numéricos para encontrar raíces de ecuaciones no lineales. Incluye definiciones de conceptos clave, tablas comparativas de métodos, pseudocódigo de los métodos de bisección y Newton-Raphson y ejemplos resueltos de encontrar raíces mediante gráficas, bisección y otros métodos.

1. Instituto Tecnológico de Los Mochis.
Carrera:
INGENIERÍA MECATRÓNICA
TRABAJO
UNIDAD 2; RAÍCES DE ECUACIONES NO LINEALES
Asignatura:
MÉTODOS NUMÉRICOS
Facilitador:
RODRÍGUEZ RODRÍGUEZ MARCO ANTONIO
Grupo:
M31
Estudiante:
VÍCTOR DE JESÚS BERNAL SANDOVAL
UNIDAD 2.
RAÍCES DE ECUACIONES NO LINEALES
20 DE OCTUBRE DEL 2013

2. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
UNIDAD 2. Raíces de ecuaciones no lineales
Actividad colaborativa en el aula.
CONTENIDO:
1.-
a) Conceptos. ................................................................................................2
b) Tabla que compara las ventajas y desventajas de cada método................3
2.- Pseudocódigo del método de bisección.............................................................4
3.- Pseudocódigo del método de Newton-Raphson...............................................5
4.- Encuentren las raíces de f(x) = -12 -21x +18x2 -2.75x3.
a) Gráficamente (en Matlab). ........................................................................6
b) Por bisección..............................................................................................7
c) Mediante falsa posición. ............................................................................8
5.- Determine la raíz real de f(x)= - 25 + 82x - 90x2 + 44x3 - 8x4 + 0.7x5.
a) Gráficamente (en Matlab). .......................................................................9
b) Usando el método de bisección con εa = 10%, Con valores iniciales
de xl = 0.5 y xu = 1. ..................................................................................10
c) Usando el método de falsa posición con los mismos datos que en b)
pero para un εa =2%.....................................................................................11
6. Determine la raíz real de f(x) = -1 + 5.5x - 4x2 + 0.5x3.
a) Gráficamente (en Matlab). .......................................................................12
b) Usando el método Newton-Raphson con εs =0.001%. ...........................13
7. Localice la primera raíz positiva de f(x) = sin(x) + cos(x2 + 1) – 1.
Donde x está en radianes.
Use cuatro iteraciones del método de la secante con valores iniciales de;
a) xi-1 = 1 y xi = 3. ...................................................................................14
b) xi-1 = 1.5 y xi = 2.5. ..........................................................................15
8. Use f(x)= -x2 + 1.8x + 25 usando x0 = 5 con εs = 0.05%.
a) En el método de iteración de punto fijo. ..................................................16
b) En el método de Newton-Raphson. ........................................................17
Página | 2

3. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
1. Definan por los siguientes conceptos:
Ecuación no lineal:
Cuando una ecuación tiene grado 1, se dice que es lineal. Entonces una ecuación no lineal es cuando es de
grado mayor a 1.
Ejemplo.
2x2+ 3x - 3=11
x3 + 4y = 14
Raíz de una función:
Cuando se habla de raíces en matemáticas, se refiere a todo elemento de una función f(x) tal que f(x)=0
Ejemplo:
La Raíz de la ecuación y=2x^2+3x-14 es 2.
f=@(x) 2*x^2+3*x-14;
f(2)
ans =
0
fzero(f,0)
ans =
2
Iteración:
En matemática se habla de métodos iterativos que resultan útiles para resolver problemas por medio de
aproximaciones sucesivas a la solución, partiendo desde una estimación inicial. Este tipo de estrategias pueden
ser más útiles que los métodos directos para resolver problemas con miles o millones de variables.
En programación, la iteración consiste en reiterar un conjunto de instrucciones o acciones con uno o varios
objetivos.
Métodos cerrados:
Estos métodos aprovechan el hecho de que una función cambia de signo en la vecindad de una raíz. A estas
técnicas se les llama métodos cerrados, o de intervalos, porque se necesita de dos valores iniciales para la raíz.
Como su nombre lo indica, dichos valores iniciales deben “encerrar”, o estar a ambos lados de la raíz.
Métodos abiertos:
Se basan en fórmulas que requieren únicamente de un solo valor de inicio x o que empiecen con un par de ellos,
pero que no necesariamente encierran la raíz.
Éstos, algunas veces divergen o se alejan de la raíz verdadera a medida que se avanza en el cálculo. Sin embargo,
cuando los métodos abiertos convergen, en general lo hacen mucho más rápido que los métodos cerrados.
Página | 1

4. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
Tabla que compara las ventajas y desventajas de cada método.
MÉTODOS
VENTAJAS
DESVENTAJAS
CERRADOS
Simple.
Bisección.
Falsa Posición.
Buena estimación del error absoluto.
Convergencia garantizada.
Convergencia lenta.
Requiere una buena estimación del
intervalo inicial (que encierra la
raíz).
Si existe más de una raíz en el
intervalo, el método permite
encontrar sólo una de ellas.
ABIERTOS
Iteración de punto
fijo.
Es simple
Es flexible
Newton - Raphson
o de la Tangente
Converge más rápido que cualquiera
de los métodos analizados hasta
ahora.
Secante
La derivada se puede aproximar
mediante una diferencia finita
dividida hacia atrás.
No está garantizada la
convergencia.
No es conveniente en el caso de
raíces múltiples.
Puede alejarse del área de interés
si la pendiente es cercana a cero.
Requiere una derivada.
Requiere dos puntos iniciales
aunque no es necesario que
encierren a la raíz.
Página | 2

5. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
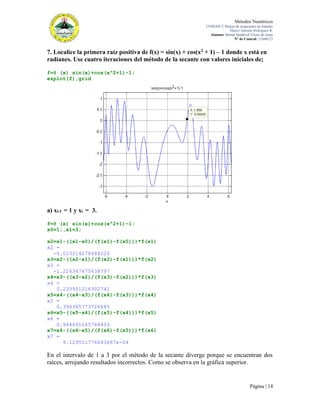
2. De acuerdo al pseudocódigo del método de bisección, hagan una propuesta
en Matlab para aplicar este algoritmo.
function[xr]= biseccion(f,xl,xu,es)
% Método de Bisección para raíces en funciones continúas dentro de un intervalo.
% Ejemplo:
% Ejecutar en la ventana de comandos:
% f=@(x)(x.^2-4);
% x = biseccion(f, 0, 5, 0.01);
% Se buscará la raíz de la función (x^2)-4, puntos iniciales a=0 y b=5, con una
tolerancia es=0.01.
fprintf('Método de la bisecciónnn');
i = 0;
if f(xl)*f(xu)>0
fprintf('Error No hay cambio de signo (%i,%i) n',xl,xu);
return
end
fprintf('Iter. t xl t t xu t t raiz n');
while (abs(xu-xl) >= es)
i=i+1;
xr=(xu + xl)/2;
if f(xr) == 0
fprintf('Raiz encontrada en x = %f n', xr);
return
end
fprintf('%2i t %f t %f t %f n', i, xl, xu, xr);
if f(xl)*f(xr)>0
xl=xr;
else
xu=xr;
end
end
f(xr);
fprintf('n La mejor aproximación a la raíz tomando una tolerancia de %f es n x
= %f con n f(x) = %f n y se realizaron %i iteracionesn',es,xr,f(xr),i-1);
end
Página | 3

6. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
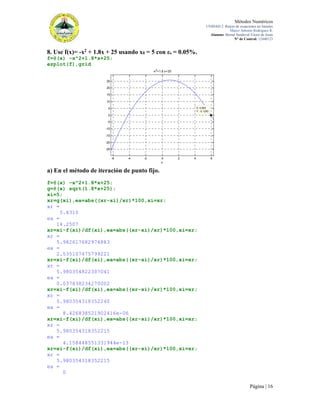
3. De acuerdo al pseudocódigo del método de Newton-Raphson, hagan una
propuesta en Matlab para aplicar este algoritmo.
(Código proporcionado por Rodríguez Rodríguez Marco Antonio)
function [x,fx,xx] = newton(f,df,x0,TolX,MaxIter)
%MÉTODO DE NEWTON-RAPHSON
%ENTRADAS
% f = función de la que se obtendrá la raíz.
% df = df(x)/dx. (Si la derivada no se proporciona, entonces
% automáticamente se usa la derivada numérica.
% x0 = es el valor estimado inicial de la solución inicial.
% TolX = El límite superior de |x(k) - x(k-1)|.
% MaxIter = El # máximo de iteraciones.
%SALIDAS
% x = El punto alcanzado por el algoritmo.
% fx = f(x(nuevo)).
% xx = la historia de x
h = 1e-4; h2 = 2*h; TolFun=eps;
if nargin == 4 && isnumeric(df)
MaxIter = TolX; TolX = x0;
x0 = df;
end
xx(1) = x0;
fx = feval(f,x0);
for k = 1: MaxIter
if ~isnumeric(df)
dfdx = feval(df,xx(k)); %derivada de la function
else dfdx = (feval(f,xx(k) + h)-feval(f,xx(k) - h))/h2; %derivada num?rica
end
dx = -fx/dfdx;
xx(k+1) = xx(k)+dx;
fx = feval(f,xx(k + 1));
if abs(fx)<TolFun || abs(dx) < TolX
break
end
end
x = xx(k + 1);
if k== MaxIter, fprintf('La mejor en %d iteracionesn',MaxIter),
end
Página | 4

7. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
4. Encuentren las raíces de f(x) = -12 -21x +18x2 -2.75x3.
a) Gráficamente (en Matlab).
f=@(x) -12-21*x+18*x.^2-2.75*x.^3;
ezplot(f),grid
-12-21 x+18 x 2-2.75 x 3
1400
1200
1000
800
600
400
200
X: -0.4208
Y: 0.2295
0
-200
-6
-4
-2
0
x
2
4
6
Usando los valores iniciales de xl = -1 y xu = 0, y un criterio de paro de 1%.
x=-1:0.001:0;
Plot(x, f(x)), grid
30
25
20
15
10
5
X: -0.415
Y: 0.0116
0
-5
-10
-15
-1
-0.9
-0.8
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
-0.1
0
Página | 6

8. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
b) Por bisección;
f=@(x) -12-21*x+18*x.^2-2.75*x.^3;
xl=-1;
xu=0;
xr=(xl+xu)/2;
f(xl),f(xr),f(xu)
ans =
29.7500
ans =
3.3438
ans =
-12
xl=xr;
xr2=(xl+xu)/2;
f(xl),f(xr2),f(xu)
ans =
3.3438
ans =
-5.5820
ans =
-12
xu=xr2;
ea=abs((xr2-xr)/xr2)*100
ea =
100
xr3=(xl+xu)/2;
f(xl),f(xr3),f(xu)
ans =
3.3438
ans =
-1.4487
ans =
-5.5820
xu=xr3;
ea=abs((xr3-xr2)/xr3)*100
ea =
33.3333
xr4=(xl+xu)/2;
f(xl),f(xr4),f(xu)
ans =
3.3438
ans =
0.8631
ans =
-1.4487
xl=xr4;
ea=abs((xr4-xr3)/xr4)*100
ea =
14.2857
xr5=(xl+xu)/2;
f(xl),f(xr5),f(xu)
ans =
0.8631
ans =
-0.3137
ans =
-1.4487
xu=xr5;
ea=abs((xr5-xr4)/xr5)*100
ea =
7.6923
ans =
0.8631
ans =
0.2695
ans =
-0.3137
xl=xr6;
ea=abs((xr6-xr5)/xr6)*100
ea =
3.7037
xr7=(xl+xu)/2;
f(xl),f(xr7),f(xu)
ans =
0.2695
ans =
-0.0234
ans =
-0.3137
xu=xr7;
ea=abs((xr7-xr6)/xr7)*100
ea =
1.8868
xr8=(xl+xu)/2;
f(xl),f(xr8),f(xu)
ans =
0.2695
ans =
0.1227
ans =
-0.0234
xl=xr8;
ea=abs((xr8-xr7)/xr8)*100
ea =
0.9346
xr9=(xl+xu)/2;
f(xl),f(xr9),f(xu)
ans =
0.1227
ans =
0.0496
ans =
-0.0234
xl=xr9;
ea=abs((xr9-xr8)/xr9)*100
ea =
0.4695
Comprobación:
Raíz aproximada
xr9
xr9 =
-0.4160
Raíz verdadera:
fzero(f,-1)
ans =
-0.4147
Raíz aproximada evaluada en f.
f(xr9)
ans =
0.0496
xr6=(xl+xu)/2;
f(xl),f(xr6),f(xu)
Página | 7

9. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
c) Mediante falsa posición.
f=@(x) -12-21*x+18*x.^2-2.75*x.^3;
xl=-1;
xu=0;
xr=xu-f(xu)*(xl-xu)/(f(xl)-f(xu));
f(xl),f(xr),f(xu)
ans =
29.7500
ans =
-4.4117
ans =
-12
xu=xr;
xr2=xu-f(xu)*(xl-xu)/(f(xl)-f(xu));
f(xl),f(xr2),f(xu)
ans =
29.7500
ans =
-1.2897
ans =
-4.4117
xu=xr2;
ea=abs((xr2-xr)/xr2)*100
ea =
24.2520
xr3=xu-f(xu)*(xl-xu)/(f(xl)-f(xu));
f(xl),f(xr3),f(xu)
ans =
29.7500
ans =
-0.3513
ans =
-1.2897
xu=xr3;
ea=abs((xr3-xr2)/xr3)*100
ea =
6.3626
xr6=xu-f(xu)*(xl-xu)/(f(xl)-f(xu));
f(xl),f(xr6),f(xu)
ans =
29.7500
ans =
-0.0066
ans =
-0.0249
xu=xr6;
ea=abs((xr6-xr5)/xr6)*100
ea =
0.1184
Comprobación;
Raíz aproximada
xr6
xr6 =
-0.4145
Raíz verdadera:
fzero(f,-1)
ans =
-0.4147
Raíz aproximada evaluada en f.
f(xr6)
ans =
-0.0066
xr4=xu-f(xu)*(xl-xu)/(f(xl)-f(xu));
f(xl),f(xr4),f(xu)
ans =
29.7500
ans =
-0.0938
ans =
-0.3513
xu=xr4;
ea=abs((xr4-xr3)/xr4)*100
ea =
1.6840
xr5=xu-f(xu)*(xl-xu)/(f(xl)-f(xu));
f(xl),f(xr5),f(xu)
ans =
29.7500
ans =
-0.0249
ans =
-0.0938
xu=xr5;
ea=abs((xr5-xr4)/xr5)*100
ea =
0.4464
Página | 8

10. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
5. Determine la raíz real de f(x)= - 25 + 82x - 90x2 + 44x3 - 8x4 + 0.7x5.
a) Gráficamente (en Matlab).
f=@(x) -25 +82*x -90*x.^2 +44*x.^3 -8*x.^4 +0.7*x.^5;
ezplot(f),grid
-25+82 x-90 x 2+44 x 3-8 x 4+0.7 x 5
4
x 10
0
X: 0.5659
Y: -0.2236
-0.5
-1
-1.5
-2
-2.5
-6
-4
-2
0
x
2
4
6
Usando los valores iniciales de xl = 0.5 y xu = 1.
x=0.5:0.001:1;
plot(x,f(x)),grid
4
3
2
1
X: 0.579
Y: -0.006632
0
-1
-2
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1
Página | 9

11. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
b) Usando el método de bisección con εa = 10%, Con valores iniciales de xl = 0.5 y
xu = 1.
f=@(x) -25+82*x-90*x.^2+44*x.^38*x.^4+0.7*x.^5;
xl=0.5;
xu=1;
xr=(xl+xu)/2;
f(xl),f(xr),f(xu)
ans =
-1.4781
ans =
2.0724
ans =
3.7000
xu=xr;
xr2=(xl+xu)/2;
f(xl),f(xr2),f(xu)
ans =
-1.4781
ans =
0.6820
ans =
2.0724
xu=xr2;
ea=abs((xr2-xr)/xr2)*100
ea =
20
f(xl),f(xr4),f(xu)
ans =
-0.2820
ans =
0.2265
ans =
0.6820
xu=xr4;
ea=abs((xr4-xr3)/xr4)*100
ea =
5.2632
Comprobación
Raíz aproximada
xr4
xr4 =
0.5938
Raíz verdadera:
fzero(f,0.5)
ans =
0.5794
Raíz aproximada evaluada en f.
f(xr4)
ans =
0.2265
xr3=(xl+xu)/2;
f(xl),f(xr3),f(xu)
ans =
-1.4781
ans =
-0.2820
ans =
0.6820
xl=xr3;
ea=abs((xr3-xr2)/xr3)*100
ea =
11.1111
xr4=(xl+xu)/2;
Página | 10

12. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
c) Usando el método de falsa posición con los mismos datos que en b) pero para un
εa =2%.
f=@(x) -25+82*x-90*x.^2+44*x.^3-8*x.^4+0.7*x.^5;
xl=0.5;
xu=1;
xr=xu-f(xu)*(xl-xu)/(f(xl)-f(xu));
f(xl),f(xr),f(xu)
ans =
-1.4781
ans =
0.9188
ans =
3.7000
xu=xr;
xr2=xu-f(xu)*(xl-xu)/(f(xl)-f(xu));
f(xl),f(xr2),f(xu)
ans =
-1.4781
ans =
0.1373
ans =
0.9188
xu=xr2;
ea=abs((xr2-xr)/xr2)*100
ea =
9.3043
xr3=xu-f(xu)*(xl-xu)/(f(xl)-f(xu));
f(xl),f(xr3),f(xu)
ans =
-1.4781
ans =
0.0182
ans =
0.1373
xu=xr3;
ea=abs((xr3-xr2)/xr3)*100
ea =
1.2885
Comprobación
Raíz aproximada
xr3
xr3 =
0.5805
Raíz verdadera:
fzero(f,0.5)
ans =
0.5794
Raíz aproximada evaluada en f.
f(xr3)
ans =
0.0182
Página | 11

13. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
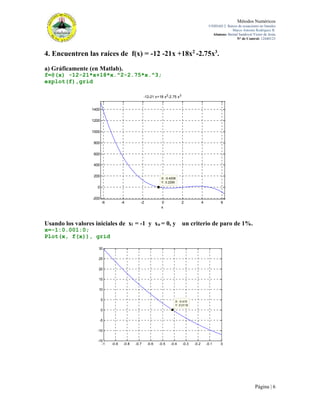
6. Determine la raíz real de f(x) = -1 + 5.5x - 4x2 + 0.5x3.
a) Graficamente (en Matlab).
f=@(x) -1+5.5*x-4*x.^2+ 0.5*x.^3;
fplot(f,[-5,8]),grid
50
X: 6.232
Y: -1.057
0
-50
-100
-150
-200
-4
-2
0
2
4
6
8
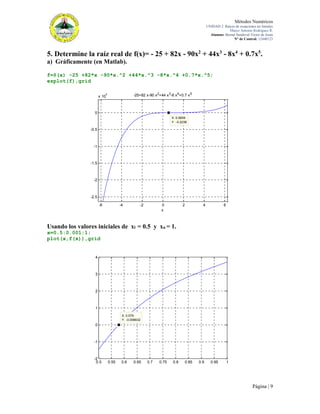
Con xi = 6 y xu = 7.
x=6:0.001:7;
plot(x,f(x)),grid
14
12
10
8
6
4
2
X: 6.306
Y: 0.001506
0
-2
-4
6
6.1
6.2
6.3
6.4
6.5
6.6
6.7
6.8
6.9
7
Página | 12

14. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
b) Usando el método Newton-Raphson con εs =0.001%.
f=@(x) -1+5.5*x-4*x.^2+ 0.5*x.^3;
xi=7;
df=@(x) 5.5-4*2*x+0.5*3*x.^2;
xr=xi-(f(xi)/df(xi));ea=abs((xr-xi)/xr)*100,xi=xr
ea =
8.783783783783781
xi =
6.434782608695652
xr=xi-(f(xi)/df(xi));ea=abs((xr-xi)/xr)*100,xi=xr
ea =
1.950853695256105
xi =
6.311651521751868
xr=xi-(f(xi)/df(xi));ea=abs((xr-xi)/xr)*100,xi=xr
ea =
0.091053261134278
xi =
6.305909785248214
xr=xi-(f(xi)/df(xi));ea=abs((xr-xi)/xr)*100,xi=xr
ea =
1.943555052127402e-04
xi =
6.305897529389212
xr=xi-(f(xi)/df(xi));ea=abs((xr-xi)/xr)*100,xi=xr
ea =
8.846152917677153e-10
xi =
6.305897529333429
xr=xi-(f(xi)/df(xi));ea=abs((xr-xi)/xr)*100,xi=xr
ea =
0
xi =
6.305897529333429
Comprobación
Raíz aproximada
xr
xr =
6.305897529333429
Raíz verdadera:
fzero(f,7)
ans =
6.305897529333430
Raíz aproximada evaluada en f.
f(xi)
ans =
0
Página | 13

15. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
7. Localice la primera raíz positiva de f(x) = sin(x) + cos(x2 + 1) – 1 donde x está en
radianes. Use cuatro iteraciones del método de la secante con valores iniciales de;
f=@ (x) sin(x)+cos(x^2+1)-1;
ezplot(f),grid
a) xi-1 = 1 y xi = 3.
f=@ (x) sin(x)+cos(x^2+1)-1;
x0=1;,x1=3;
x2=x1-((x1-x0)/(f(x1)-f(x0)))*f(x1)
x2 =
-0.023214278484220
x3=x2-((x2-x1)/(f(x2)-f(x1)))*f(x2)
x3 =
-1.226347475638797
x4=x3-((x3-x2)/(f(x3)-f(x2)))*f(x3)
x4 =
0.233951216302741
x5=x4-((x4-x3)/(f(x4)-f(x3)))*f(x4)
x5 =
0.396365773726685
x6=x5-((x5-x4)/(f(x5)-f(x4)))*f(x5)
x6 =
0.944691165764433
x7=x6-((x6-x5)/(f(x6)-f(x5)))*f(x6)
x7 =
9.129551776043687e-04
En el intervalo de 1 a 3 por el método de la secante diverge porque se encuentran dos
raíces, arrojando resultados incorrectos. Como se observa en la gráfica superior.
Página | 14

16. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
b) xi-1 = 1.5 y xi = 2.5.
f=@ (x) sin(x)+cos(x^2+1)-1;
x0=1.5;,x1=2.5;
x2=x1-((x1-x0)/(f(x1)-f(x0)))*f(x1)
x2 =
2.356928734995134
x3=x2-((x2-x1)/(f(x2)-f(x1)))*f(x2)
x3 =
2.547287160429604
x4=x3-((x3-x2)/(f(x3)-f(x2)))*f(x3)
x4 =
2.526339088383083
x5=x4-((x4-x3)/(f(x4)-f(x3)))*f(x4)
x5 =
2.532106931631685
x6=x5-((x5-x4)/(f(x5)-f(x4)))*f(x5)
x6 =
2.532213337592640
x7=x6-((x6-x5)/(f(x6)-f(x5)))*f(x6)
x7 =
2.532212552600018
x8=x7-((x7-x6)/(f(x7)-f(x6)))*f(x7)
x8 =
2.532212552702561
x9=x8-((x8-x7)/(f(x8)-f(x7)))*f(x8)
x9 =
2.532212552702561
Comprobación;
Raíz aproximada
x9
x9 =
2.532212552702561
Raíz verdadera:
fzero(f,2.5)
ans =
2.532212552702561
Raíz aproximada evaluada en f.
f(x9)
ans =
4.440892098500626e-16
Página | 15

17. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
8. Use f(x)= -x2 + 1.8x + 25 usando x0 = 5 con εs = 0.05%.
f=@(x) -x^2+1.8*x+25;
ezplot(f),grid
-x 2+1.8 x+25
25
20
15
10
X: 5.993
Y: -0.1283
5
0
-5
-10
-15
-20
-25
-6
-4
-2
0
x
2
4
6
a) En el método de iteración de punto fijo.
f=@(x) -x^2+1.8*x+25;
g=@(x) sqrt(1.8*x+25);
xi=5;
xr=g(xi),ea=abs((xr-xi)/xr)*100,xi=xr;
xr =
5.8310
ea =
14.2507
xr=xi-f(xi)/df(xi),ea=abs((xr-xi)/xr)*100,xi=xr;
xr =
5.982617682974883
ea =
2.535107475799221
xr=xi-f(xi)/df(xi),ea=abs((xr-xi)/xr)*100,xi=xr;
xr =
5.980354822307041
ea =
0.037838234270002
xr=xi-f(xi)/df(xi),ea=abs((xr-xi)/xr)*100,xi=xr;
xr =
5.980354318352240
ea =
8.426838521902416e-06
xr=xi-f(xi)/df(xi),ea=abs((xr-xi)/xr)*100,xi=xr;
xr =
5.980354318352215
ea =
4.158448551331944e-13
xr=xi-f(xi)/df(xi),ea=abs((xr-xi)/xr)*100,xi=xr;
xr =
5.980354318352215
ea =
0
Página | 16

18. Métodos Numéricos
UNIDAD 2. Raíces de ecuaciones no lineales
Marco Antonio Rodríguez R.
Alumno: Bernal Sandoval Victor de Jesús
N° de Control: 12440123
b) En el método de Newton-Raphson.
f=@(x) -x^2+1.8*x+25;
df=@(x) -2*x+1.8;
xi=5;
xr=xi-f(xi)/df(xi),ea=abs((xr-xi)/xr)*100,xi=xr;
xr =
6.097560975609756
ea =
18.000000000000004
xr=xi-f(xi)/df(xi),ea=abs((xr-xi)/xr)*100,xi=xr;
xr =
5.981675842098637
ea =
1.937335565654146
xr=xi-f(xi)/df(xi),ea=abs((xr-xi)/xr)*100,xi=xr;
xr =
5.980354490187754
ea =
0.022094876032039
xr=xi-f(xi)/df(xi),ea=abs((xr-xi)/xr)*100,xi=xr;
xr =
5.980354318352218
ea =
2.873333700232322e-06
xr=xi-f(xi)/df(xi),ea=abs((xr-xi)/xr)*100,xi=xr;
xr =
5.980354318352215
ea =
4.455480590712798e-14
xr=xi-f(xi)/df(xi),ea=abs((xr-xi)/xr)*100,xi=xr;
xr =
5.980354318352215
ea =
0
Comprobación;
Raíz aproximada
xr
xr =
5.980354318352215
Raíz verdadera:
fzero(f,5)
ans =
5.980354318352215
Raíz aproximada evaluada en f.
f(xr)
ans =
0
Página | 17