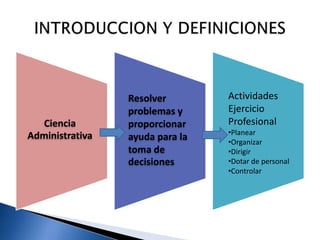
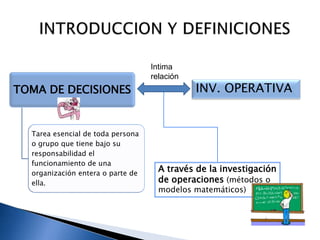
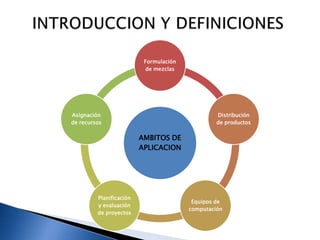
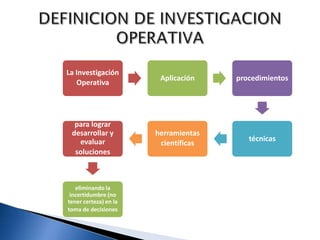
El documento detalla el uso de la investigación operativa y modelado matemático en la toma de decisiones y optimización de recursos en empresas. Se describe un proceso sistemático en cuatro pasos que incluye la definición de problemas, modelado, resolución y presentación de resultados. Se enfatiza la importancia de funciones objetivo y restricciones en la programación lineal para maximizar soluciones empresariales.

1. UNIVERSIDAD TECNICA DE AMBATO
FACULTAD DE CONTABILIDAD Y AUDITORIA
ING. MARCO GUACHIMBOZA
mguachimboza@hotmail.com
Febrero – Agosto 2013

2. Ciencia
Administrativa
Resolver
problemas y
proporcionar
ayuda para la
toma de
decisiones
Actividades
Ejercicio
Profesional
•Planear
•Organizar
•Dirigir
•Dotar de personal
•Controlar

3. TOMA DE DECISIONES
Tarea esencial de toda persona
o grupo que tiene bajo su
responsabilidad el
funcionamiento de una
organización entera o parte de
ella.
INV. OPERATIVA
A través de la investigación
de operaciones (métodos o
modelos matemáticos)
Intima
relación

4. AMBITOS DE
APLICACION
Formulación
de mezclas
Distribución
de productos
Equipos de
computación
Planificación
y evaluación
de proyectos
Asignación
de recursos

5. La Investigación
Operativa
Aplicación procedimientos
técnicas
herramientas
científicas
para lograr
desarrollar y
evaluar
soluciones
eliminando la
incertidumbre (no
tener certeza) en la
toma de decisiones

7. Paso 2. Modelado matemático
Verbaliza un problema para posteriormente
cuantificarlo transformando las expresiones verbales
en expresiones matemáticas. El proceso del
modelado matemático consta de cuatro pasos:
Paso 1. Definición del problema
Quizás la parte más importante de todo el proceso. Es
importante que el problema esté claramente definido
antes de invertir una gran cantidad de trabajo y energía
en resolverlo.

8. Modelo matemático
2.1. Identificar las variables de decisión
Un paso crucial en la construcción de un modelo
matemático es determinar aquellos factores sobre
los qué el decidor tiene control,
¿Qué es lo que hay que decidir? o ¿sobre qué
elementos tenemos control?

9. Modelo matemático
2.2. Identificar la función objetivo
Es encontrar el modo de optimizar alguna medida ¿qué es lo
que queremos conseguir? o Si yo fuera el jefe de esta
empresa, ¿qué me interesaría más?
2.3. identificar las restricciones
limitan nuestra decisión. Ejemplos: los recursos disponibles
(trabajadores, máquinas, material, etc.); fechas límite
impuestas por los contratos; restricciones impuestas por la
naturaleza del problema
2.4. Traducir los elementos anteriores a un modelo matemático
Una vez identificados los elementos básicos hay que expresarlos
matemáticamente.

10. Paso 3. Resolución del modelo
Aplicar los algoritmos y métodos matemáticos
diseñados para su resolución.
Paso 4. Presentación/Implementación de los
resultados
•Preparar informes y/o presentaciones.
Los decisores deben comprender
completamente las soluciones
•Vigilar el proceso de implementación.
Una vez implementada la solución, debe
ser supervisada de forma continua

11. Introducción.
En cualquier empresa, muchas de las decisiones que se toman tienen por
objeto hacer el mejor uso posible (optimización) de los recursos de la
misma. Por recursos de una empresa entendemos la maquinaria que ésta
posea, sus trabajadores, capital financiero, instalaciones, y las materias
primas de que disponga. Tales recursos pueden ser usados para fabricar
productos (electrodomésticos, muebles, comida, ropa, etc.) o servicios
(horarios de producción, planes de marketing y publicidad, decisiones
financieras, etc.).

12. 1. A partir de los recursos disponibles, determinar las
unidades a producir de cada bien de forma que se
maximice el beneficio de la empresa.
2. Elegir materias primas en procesos de alimentación, para
obtener mezclas con unas determinadas propiedades al
mínimo coste.
3. Determinar el sistema de distribución que minimice el
coste total de transporte, desde diversos almacenes a
varios puntos de distribución.
4. Desarrollar un plan de producción que, satisfaciendo las
demandas futuras de los productos de una empresa,
minimice al mismo tiempo los costes totales de producción
e inventario.

13. Es un proceso sistemático y matemático de enfocar un problema para lograr
una solución óptima o la mejor posible de entre varias, empleando una
función objetivo (propósito del problema), un conjunto de restricciones
lineales y una condición de eliminar valores negativos. Los problemas de
programación lineal planteados y resueltos con cualquiera de los métodos
deberán cumplir con tres soluciones necesarias y suficientes.
a) Función Objetivo.- Es la ecuación que expresa la cantidad que va ha ser maximizada o
minimizada. Z = C1X1+C2X2+C3X3+…………+ CnXn
Se acostumbra a realizar:
Z (MAX), para la maximización; Z (MIN), para la minimización
Xj, simboliza matemáticamente a las variables de decisión.
En la ecuación Cj, matemáticamente, simboliza el coeficiente de la variable j en la Función
Objetivo. Son datos relevantes, insumos incontrolables ya conocidos. En la Función Objetivo
representan la cantidad con la cual contribuye cada unidad de la variable j, al valor total
deseado en el objetivo, pudiendo ser márgenes de beneficios, precios, costos unitarios, etc.

14. b) Limitaciones o Restricciones.- Es el conjunto de inecuaciones o ecuaciones
que nos expresan las condiciones del problema, denominadas también
coeficientes técnicos de producción
El sistema de ecuaciones se presenta:
a11X1 + a12X2 + a13X3 + ………………….. + a1nXn T1 b1
a21X1 + a22X2 + a23X3 + ………………….. + a2nXn T2 b2
a31X1 + a32X2 + a33X3 + ………………….. + a3nXn T3 b3
. . .
. . .
. . .
am1X1 + am2X2 + am3X3 + ……………….. + amnXn Tm bm

15. En donde:
a11, a12, a13, ……………, am
.
. Coeficientes técnicos
.
am1, am2, am3, ……………, amn
X1, X2, X3, …………….., Xn: Son las variables o incógnitas del
problema.
T1, T2, T3, ……………..., Tm: Son los límites de l sistema, se
representan >=, <=, =
b1, b2, b3, ………………., bm: son los valores máximos o mínimos.
Condición de no negatividad.- Xn >= 0