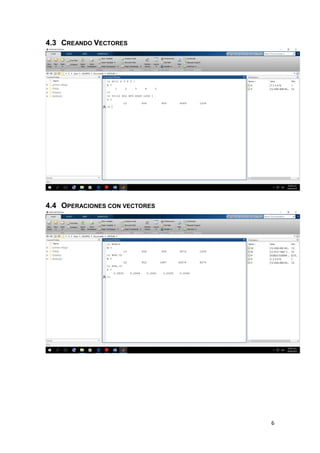
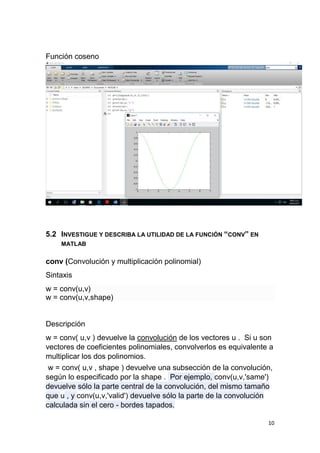
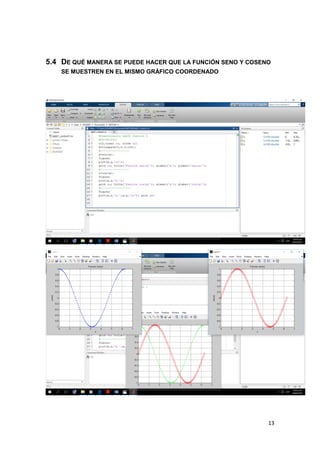
Este documento describe los procedimientos realizados en el laboratorio de Matlab, incluyendo la creación de variables, vectores, matrices, operaciones con polinomios y gráficas de funciones trigonométricas. También incluye preguntas sobre funciones como "conv" y cómo mostrar la función seno y coseno en el mismo gráfico.

1. UNIVERSIDAD NACIONAL DE TRUJILLO
FACULTAD DE INGENIERÍA
ESCUELA
ING MECATRONICA
CURSO
Control I
PROFESOR
Ing Luis Vargas
ALUMNO
Narciso Vera Wily Marco
Ciclo
VII
2017

2. 2
INDICE
1 RESUMEN........................................................................................................................... 3
2 OBJETIVOS ........................................................................................................................ 3
2.1 Objetivo Principal........................................................................................................ 3
2.2 Objetivos secundarios................................................................................................ 3
3 MARCO TEORICO............................................................................................................. 4
4 PROCEDIMIENTO............................................................................................................. 5
4.1 Creación de variables ................................................................................................ 5
4.2 Operaciones Básicas................................................................................................. 5
4.3 Creando Vectores....................................................................................................... 6
4.4 Operaciones con vectores ........................................................................................ 6
4.5 Creación con matrices............................................................................................... 7
4.6 Operaciones con Polinomios.................................................................................... 7
4.7 Graficas........................................................................................................................ 8
4.8 Modificador de plot..................................................................................................... 8
5 Cuestionario ........................................................................................................................ 9
5.1 Primera pregunta........................................................................................................ 9
5.2 Investigue y describa la utilidad de la función “conv” en matlab....................... 10
5.2.1 Ejemplos ............................................................................................................ 11
5.3 ¿a qué le llamamos un archivo m?, redacte uno que cumpla lo indicado en la
primera pregunta de este cuestionario.............................................................................. 11
5.4 De qué manera se puede hacer que la función seno y coseno se muestren en
el mismo gráfico coordenado.............................................................................................. 13
6 Referencia ......................................................................................................................... 14

3. 3
1 RESUMEN
En el presente informe se expresa mediante capturas de pantallas
los procesos del laboratorio en Matlab donde se desarrolla la
creación de variables, creación de vectores, operaciones con
vectores, creación de matrices, opresiones con polinomios y mostrar
graficas de funciones trigonométricas
2 OBJETIVOS
2.1 OBJETIVO PRINCIPAL
Familiarización con el manejo del software Matlab como
herramienta de ayuda para el cálculo
2.2 OBJETIVOS SECUNDARIOS
Identificar las diferentes funciones utilizadas para el cálculo
matemático matricial y polinomio.
Utilizar las herramientas de matlab para la generación de gráficos
de funciones y puntos coordenados

4. 4
3 MARCO TEORICO
MATLAB es un entorno de computación y desarrollo de aplicaciones
totalmente integrado orientado para llevar a cabo proyectos en donde
se encuentren implicados elevados cálculos matemáticos y la
visualización gráfica de los mismos.
MATLAB integra análisis numérico, cálculo matricial, proceso de
señal y visualización gráfica en un entorno completo donde los
problemas y sus soluciones son expresados del mismo modo en que
se escribirían adicionalmente, sin necesidad de hacer uso de la
programación tradicional.
MATLAB dispone también en la actualidad de un amplio abanico de
programas de apoyo especializados, denominados Toolboxes, que
extienden significativamente el número de funciones incorporadas en
el programa principal. Estos Toolboxes cubren en la actualidad
prácticamente casi todas las áreas principales en el mundo de la
ingeniería y la simulación, destacando entre ellos el 'toolbox' de
proceso de imágenes, señal, control robusto, estadística, análisis
financiero, matemáticas simbólicas, redes neurales, lógica difusa,
identificación de sistemas, simulación de sistemas dinámicos, etc. es
un entorno de cálculo técnico, que se ha convertido en estándar de
la industria, con capacidades no superadas en computación y
visualización numérica.
De forma coherente y sin ningún tipo de fisuras, integra los requisitos
claves de un sistema de computación técnico: cálculo numérico,
gráficos, herramientas para aplicaciones especificas y capacidad de
ejecución en múltiples plataformas. Esta familia de productos
proporciona al estudiante un medio de carácter único, para resolver
los problemas más complejos y difíciles.

5. 5
4 PROCEDIMIENTO
4.1 CREACIÓN DE VARIABLES
4.2 OPERACIONES BÁSICAS

6. 6
4.3 CREANDO VECTORES
4.4 OPERACIONES CON VECTORES

7. 7
4.5 CREACIÓN CON MATRICES
4.6 OPERACIONES CON POLINOMIOS

8. 8
4.7 GRAFICAS
4.8 MODIFICADOR DE PLOT

9. 9
5 CUESTIONARIO
5.1 PRIMERA PREGUNTA
Utilizando la función plot y sus modificadores haga que se muestre
una figura con la función seno es decir t vs y pero formado por
círculos de color rojo, y en otra ventana que se muestre la figura de
la función coseno (puede crear otro vector z con los valores de la
función coseno de t) como una línea de color verde
Función Seno

10. 10
Función coseno
5.2 INVESTIGUE Y DESCRIBA LA UTILIDAD DE LA FUNCIÓN “CONV” EN
MATLAB
conv (Convolución y multiplicación polinomial)
Sintaxis
w = conv(u,v)
w = conv(u,v,shape)
Descripción
w = conv( u,v ) devuelve la convolución de los vectores u . Si u son
vectores de coeficientes polinomiales, convolverlos es equivalente a
multiplicar los dos polinomios.
w = conv( u,v , shape ) devuelve una subsección de la convolución,
según lo especificado por la shape . Por ejemplo, conv(u,v,'same')
devuelve sólo la parte central de la convolución, del mismo tamaño
que u , y conv(u,v,'valid') devuelve sólo la parte de la convolución
calculada sin el cero - bordes tapados.

11. 11
5.2.1 Ejemplos
.
5.3 ¿A QUÉ LE LLAMAMOS UN ARCHIVO M?, REDACTE UNO QUE CUMPLA
LO INDICADO EN LA PRIMERA PREGUNTA DE ESTE CUESTIONARIO
Archivo m
Un fichero .m puede llamar a otros archivo .m y ficheros de
comandos pueden ser llamados desde ficheros de funciones. En
estos casos es importante tener en cuenta la definición de las
variables a utilizar, en la línea de que tengan un tratamiento local o
global. Por defecto, Matlab considera las variables locales, es decir,
aunque varias funciones tengan la variable x, ésta es diferente en
cada caso a no ser que haya sido definida como global
Son ficheros de texto sin formato y que pueden crearse a partir de
un editor de textos, no obstante, lo mejor es utilizar el editor del
propio programa al que se accede por defecto al abrir un nuevo
fichero

12. 12

13. 13
5.4 DE QUÉ MANERA SE PUEDE HACER QUE LA FUNCIÓN SENO Y COSENO
SE MUESTREN EN EL MISMO GRÁFICO COORDENADO

14. 14
6 REFERENCIA
https://es.mathworks.com/help/matlab/ref/conv.html
http://www.monografias.com/trabajos5/matlab/matlab.shtml
http://www2.caminos.upm.es/Departamentos/matematicas/Fdistanci
a/PIE/matlab/temasmatlab/TEMA%204.pdf