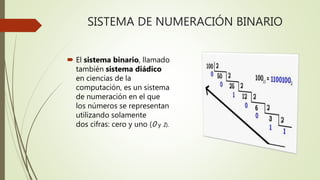
Este documento explica los sistemas numéricos binario, octal, decimal y hexadecimal. Define cada sistema y describe sus características como la base y los símbolos utilizados. También cubre temas como la conversión entre sistemas numéricos, fracciones en cada sistema y la representación de números enteros y no enteros. El objetivo es que los lectores comprendan estos diferentes sistemas y puedan convertir números de un sistema a otro.

1. UNIVERSIDAD AMERICANA DE PANAMÁ
APLICACIONES DE MICROCOMPUTADORES
JEANDERYS RIQUELME
8-9461719
PROFESORA
SUSAN JANETTE OLIVA
TEMA
LOS SISTEMA NUMÉRICOS

2. ÍNDICE
 Introducción
 Objetivo
 Sistema Numérico
 Clasificación de sistema numérico
-Sistema Numérico Binario
-Sistema Numérico Octal
-Sistema Numérico Decimal
-Sistema Numérico Hexadecimal
 Conversión de sistema numérico
 Conclusión
 Infografía

3. INTRODUCCIÓN
 A lo largo de la evolución del hombre, la necesidad de contar ha sido
indispensable. Muchos utilizaron sus dedos de las manos y de los pies como
instrumento de cálculo, contando así hasta veinte. Con los sistemas de numeración
tenemos una manera simbólica, distinta de la escritura ordinaria, para representar a
los números. Un sistema de numeración no es más que un conjunto de símbolos y
reglas degeneración que permiten construir todos los números válidos en
el sistema y aunque distintas culturas adoptaron sistemas de numeración propios,
el sistema decimal indo arábigo que, como su nombre lo indica, tiene por base al
diez es usado en la mayor parte de los países. En todos ellos se observa un método
común

4. OBJETIVO
 Conocer el sistema numérico binario y comprender la necesidad de su nacimiento.
 Repasar los métodos de representación numérica de los sistemas: decimal, binario,
octal y hexadecimal, para números enteros y fraccionarios.
 Discutir los métodos de conversión entre los sistemas numéricos

5. SISTEMAS NUMÉRICOS
Un sistema de numeración es el conjunto de
símbolos y reglas que se utilizan para la
representación de datos numéricos o cantidades. Se
caracteriza por su base, que es el número de
símbolos distintos que utiliza y además es el
coeficiente que determina cuál es el valor de cada
símbolo dependiendo de la posición que ocupe.

6.  Los actuales sistemas de
numeración son netamente
posicionales, en los que el
valor relativo que representa
cada símbolo o cifra
depende de su valor
absoluto y de la posición que
ocupa dicha cifra con
respecto a la coma decimal.

7. LA COMA DECIMAL
 La coma decimal (,) que
separa la parte entera de la
parte fraccionaria, en
ambientes informáticos,
está representada por el
punto decimal (.).

9. SISTEMA DE NUMERACIÓN BINARIO
 El sistema binario, llamado
también sistema diádico
en ciencias de la
computación, es un sistema
de numeración en el que
los números se representan
utilizando solamente
dos cifras: cero y uno (0 y 1).

10. MULTIPLOS DE BITS
 Para la medida de unidades de información representada en binario, se
utilizan una serie de múltiplos de bit que poseen nombre propio:
 Nibble o Cuarteto: Es el conjunto de cuatro bits (1001).
 Byte u Octeto: Es el conjunto de ocho bits (10101010).
 Kilobyte (Kb): Es el conjunto de 2^10 bits (1.024 * 8 bits)
 Megabyte (Mb): Es el conjunto de 2^20 Kilobytes bits (1.0242 * 8 bits)
 Gigabyte (Gb): Es el conjunto de 2^30 Megabytes bits (1.0243 * 8 bits)
 Terabyte (Tb): Es el conjunto de 2^40 Gigabytes bits (1.0244 * 8 bits)

11. SISTEMA DE NUMERACIÓN OCTAL
 El sistema de numeración octal es un sistema de numeración en
base 8, una base que es potencia exacta de 2 o de la numeración
binaria. Esta característica hace que la conversión a binario o
viceversa sea bastante simple. El sistema octal usa 8 dígitos (0, 1, 2,
3, 4, 5, 6, 7) y cada dígito tiene el mismo valor que en el sistema de
numeración decimal. El teorema fundamental aplicado al sistema
octal sería el siguiente:

12. FRACCIONES
 La numeración octal es tan
buena para operar con
fracciones, puesto que el
único factor primo para sus
bases es 2. Todas las
fracciones que tengan un
denominador distinto de una
potencia de 2 tendrán un
desarrollo octal periódico.
Fracción Octal Resultado en octal
1/2 1/2 0,4
1/3 1/3
0,25252525
periódico
1/4 1/4 0,2
1/5 1/5
0,14631463
periódico
1/6 1/6
0,125252525
periódico
1/7 1/7 0,111111
1/8 1/10 0,1
1/9 1/11
0,07070707
periódico
1/10 1/12
0,063146314
periódico

13. SISTEMA DE NUMERACIÓN DECIMAL
 es un sistema de numeración posicional en el que
las cantidades se representan utilizando como base
aritmética las potencias del número diez. El conjunto de
símbolos utilizado (sistema de numeración arábiga) se
compone de diez cifras : cero (0) - uno (1) - dos (2) - tres (3) -
cuatro (4) - cinco (5) - seis (6) - siete (7) - ocho (8)
y nueve (9).

14. NOTACIÓN DECIMAL
PARA NÚMEROS
ENTEROS
 . Para números enteros,
comenzando de derecha a
izquierda, el primer dígito le
corresponde el lugar de las
unidades, de manera que el dígito
se multiplica por 100 (es decir 1) ; el
siguiente dígito corresponde a
las decenas (se multiplica por 101);
el siguiente a las centenas (se
multiplica por 102=100); el
siguiente a las unidades de
millar (se multiplica por 103=1000)
y así sucesivamente. El valor del
número entero es la suma de los
dígitos multiplicados por las
correspondientes potencias de diez
según su posición.

15. PARA NÚMEROS NO ENTEROS
 Se utiliza las potencias negativas
de diez, y un separador
decimal entre la parte entera y la
parte fraccionaria, que queda a
la derecha. El primer dígito a la
derecha del separador decimal
corresponde a las décimas (se
multiplica por 10-1=0,1); el
siguiente a las centésimas (se
multiplica por 10-2=0,01); el
siguiente a las milésimas (se
multiplica por 10-3=0,001) y así
sucesivamente, nombrándose
estos según su posición,
utilizando el partitivo decimal
correspondiente.

16. SISTEMA HEXADECIMAL
 El sistema hexadecimal
emplea la base 16. Así,
tiene 16 posibles símbolos
digitales. Utiliza los dígitos
del 0 al 9, más las letras A,
B, C, D, E y F como sus 16
símbolos digitales.

17. FRACCIONES
Fracción Hexadecimal Resultado en hexadecimal
1/2 1/2 0,8
1/3 1/3 0,5 periodo
1/4 1/4 0,4
1/6 1/6 0,2A periodo
1/7 1/7 0,249 periodo
1/8 1/8 0,2
1/9 1/9 0,1C7 periodo
1/10 1/A 0,19 periodo
1/11 1/B 0,1745D periodo
1/12 1/C 0,15 periodo
1/13 1/D 0,13B periodo
1/14 1/E 0,1249 periodo
1/15 1/F 0,1 periodo
1/16 1/10 0,1
 Como el único factor primo
de 16 es 2, todas las
fracciones que no tengan
una potencia de 2 en el
denominador tendrán un
desarrollo hexadecimal
periódico.

18. CONVERSIÓN DEL SISTEMA
NÚMERICO

19. CONVERSIÓN DE UN NUMERO DECIMAL A
BINARIO
 Transformemos el numero 42 a numero
binario
1. Dividimos el numero 42 entre 2

2. Dividimos el cociente obtenido por 2
y repetimos el mismo procedimiento
hasta que el cociente sea 1.

3. El numero binario lo formamos
tomando el primer dígito el ultimo
cociente, seguidos por los residuos
obtenidos en cada división,
seleccionándolos de derecha a
izquierda, como se muestra en el
siguiente esquema.

20. CONVERSIÓN DE UN NUMERO BINARIO A UN
NUMERO DECIMAL
 1. Tomamos los valores de posición
correspondiente a las columnas
donde aparezcan únicamente unos.
 2. Sumamos los valores de posición
para identificar el numero decimal
equivalente

21. CONVERSIÓN DE UN NUMERO DECIMAL A
OCTAL
 Convertir el numero decimal 323.625 a el sistema de
numeración Octal
1. Se toma el numero entero y se divide entre 8
repetidamente hasta que el dividendo sea menor que
el divisor, para colocar entonces el numero 0 y pasar
el dividendo a formar el primer dígito del numero
equivalente en decimal

2. Se toma la parte fraccionaria del numero decimal y
la multiplicamos por 8 sucesivamente hasta que el
producto no tenga números fraccionarios.

3. Pasamos la parte entera del producto a formar el
dígito correspondiente

4. Al igual que los demás sistemas , el numero
equivalente en el sistema decimal , esta formado por
la unión del numero entero equivalente y el numero
fraccionario equivalente.

22. CONVERSIÓN DE UN NUMERO OCTAL A
BINARIO
 La ventaja principal del sistema de
numeración Octal es la facilidad
conque pueden realizarse la
conversión entre un numero binario
y octal. A continuación mostraremos
un ejercicio que ilustrará la teoría.
Por medio de este tipo de
conversiones, cualquier numero
Octal se convierte a binario de
manera individual. En este ejemplo,
mostramos claramente el
equivalente 100 111 010 en binario
de cada numero octal de forma
individual.

23. CONVERSIÓN DE UN NUMERO DECIMAL A UN
NUMERO HEXADECIMAL

Convertir el numero 250.25 a Hexadecimal
1. Se toma la parte entera y se divide sucesivamente por el
numero decimal 16 (base) hasta que el cociente sea 0.

2. Los números enteros resultantes de los cocientes,
pasarán a conformar el numero hexadecimal
correspondiente, teniendo en cuenta que el sistema de
numeración hexadecimal posee solo 16 símbolos, donde
los números del 10 hasta el 15 tienen símbolos alfabéticos
que ya hemos explicado

3. La parte fraccionaria del numero a convertir se
multiplica por 16 (Base) sucesivamente hasta que el
producto resultante no tenga parte fraccionaria

4. Al igual que en los sistemas anteriores, el numero
equivalente se forma, de la unión de los dos números
equivalentes, tanto entero como fraccionario, separados
por un punto que establece la diferencia entre ellos.

24. CONVERSIÓN DE UN NUMERO HEXADECIMAL
A UN NUMERO DECIMAL
 Convertir el numero hexadecimal 2B6 a
su equivalente decimal.
1. Multiplicamos el valor de posición de
cada columna por el dígito hexadecimal
correspondiente.

2. El resultado del número decimal
equivalente se obtiene, sumando todos
los productos obtenidos en el paso
anterior.

25. CONCLUSIÓN
 Un sistema de numeración está definido por la elección arbitraria de una base de
numeración (esta base es igual al número de símbolos, llamados cifras, que se
utilizarán para representar los números) y por ciertas reglas de posición. La
base a elegida debe ser un número natural superior a 1; una vez fijada la base, es
necesario elegir a signos diferentes y a nombres diferentes para representar y
nombrar los primeros números inferiores a a.
 En el caso en que a=10 se trata del sistema de numeración decimal, sistema
utilizado de manera general, y cuyo origen es casi con seguridad el número de
dedos de las manos. Los símbolos utilizados son, en este caso, las cifras 0, 1, 2, 3, 4,
5, 6, 7, 8 y 9.

26. INFOGRAFÍA
 https://es.wikipedia.org/wiki/Sistema_hexadecimal
 http://www.unet.edu.ve/~nduran/Lab_Ins_con/Sistemas_Digitales_Introduccion.pdf
 http://www.ladelec.com/teoria/electronica-digital/343-conversiones-de-sistemas-
de-numeracion