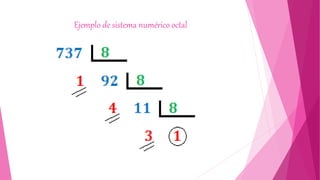
Este documento discute los sistemas numéricos utilizados en computadoras, incluidos los sistemas binario, octal, decimal y hexadecimal. Explica cómo cada sistema tiene una base diferente de dígitos y cómo representar y convertir números entre sistemas, como convertir un número binario a decimal multiplicando cada bit por una potencia de 2.

1. Profesora:
Susan Oliva
Asignatura:
Aplicaciones en Microcomputadoras
Tema:
Sistemas Numéricos y de Conversión de las computadora
Estudiante:
Andreyris Martínez 8-844-1777

2. índice
 Introducción
 Objetivos
 Sistemas numéricos
 Sistema numérico binario
 Sistema numérico octal
 Sistema numérico decimal
 Sistema numérico hexadecimal
 Conversión de binario a decimal
 Conversión de decimal a binario
 Conversión de decimal a octal
 Conversión de hexadecimal a binario
 Conversión de binario a hexadecimal
 Conclusión
 Infografía

3. introducción
 Un sistema de numeración es el conjunto de símbolos y reglas que se utilizan para la
representación de datos numéricos o cantidades. Un sistema de numeración se caracteriza
por su base, que es el número de símbolos distintos que utiliza y además es el coeficiente
que determina cuál es el valor de cada símbolo dependiendo de la posición que ocupe.
 Los actuales sistemas de numeración son netamente posicionales, en los que el valor
relativo que representa cada símbolo o cifra depende de su valor absoluto y de la posición
que ocupa dicha cifra con respecto a la coma decimal. La coma decimal (,) que separa la
parte entera de la parte fraccionaria, en ambientes informáticos, está representada por el
punto decimal (.).

4. objetivo
 Comprender el manejo de números y operaciones aritméticas desde un lenguaje de
programación de bajo nivel.
 Repasar los métodos de representación numérica de los sistemas: decimal, binario, octal y
hexadecimal, para números enteros y fraccionarios.
 Discutir los métodos de conversión entre los sistemas numéricos de nuestro interés, tanto
para números enteros y fraccionarios.
 Comprender la representación de números binarios con signo empleando la notación
complemento a 2.
 Repasar las operaciones aritméticas elementales: suma, resta, multiplicación y división.
 Concepto de punto fijo y flotante.
 Comprender la necesidad de codificar la información

5. sistema numérico
Sistema de Numeración es un conjunto de dígitos que sirven para representar una cantidad
contable.
El nombre del sistema de numeración que se trate serán los diferentes dígitos posibles para tal
representación.
Así también los sistemas de numeración se les llama base, de tal manera que el sistema de
numeración binario, también se le llama base 2.
Los sistemas de numeración más utilizados en electrónica son:
 Binario o Base 2 (0, 1)
 Octal o Base 8 (0, 1, 2, 3, 4, 5, 6, 7)
 Hexadecimal o Base 16 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F)
 Decimal o Base 10 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)

6. Sistema numérico binario
El sistema de numeración más simple que usa la notación posicional es el sistema de
numeración binario. Este sistema, como su nombre lo indica, usa solamente dos dígitos
(0,1).

7. Sistema numérico octal
El sistema de numeración octal es también muy usado en la computación por tener una base que
es potencia exacta de 2 o de la numeración binaria.
Esta característica hace que la conversión a binario o viceversa sea bastante simple.
El sistema octal usa 8 dígitos (0,1,2,3,4,5,6,7) y tienen el mismo valor que en el sistema de
numeración decimal.
Como el sistema de numeración octal usa la notación posicional entonces para el número
3452.32q tenemos:
2*(80) + 5*(81) + 4*(82) + 3*(83) + 3*(8-1) + 2*(8-2) = 2 + 40 + 4*64 + 64 + 3*512 + 3*0.125 +
2*0.015625 = 2 + 40 + 256 + 1536 + 0.375 + 0.03125 = 1834 + 40625d entonces, 3452.32q =
1834.40625d
Los números octales pueden construirse a partir de números binarios agrupando cada tres dígitos
consecutivos de estos últimos (de derecha a izquierda) y obteniendo su valor decimal.
Por ejemplo, el número binario para 74 (en decimal) es 1001010 (en binario), lo agruparíamos
como 1 001 010. De modo que 74 en octal es 112.
Es posible que la numeración octal se usara en el pasado en lugar de la decimal, por ejemplo,
para contar los espacios interdigitales o los dedos distintos de los pulgares.

8. Ejemplo de sistema numérico octal

9. Sistema de numero decimal
El sistema de numeración decimal es el más usado, tiene como base el número 10, o sea
que posee 10 dígitos (o símbolos) diferentes (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). El sistema de
numeración decimal fue desarrollado por los hindúes, posteriormente lo introducen los
árabes en Europa, donde recibe el nombre de sistema de numeración decimal o arábigo. Si
se aplica la notación posicional al sistema de numeración decimal entonces el dígito
número n tiene el valor: (10n)* A
Este valor es positivo y es mayor o igual que uno si el dígito se localiza a la izquierda del
punto decimal y depende del dígito A, en cambio el valor es menor que uno si el dígito se
localiza a la derecha del punto decimal.
Por ejemplo, el número 3489.125 expresado en la notación posicional es:
primero 9 * (100) = 9 --------- primero 1*(10-1) = 0.1
segundo 8 * (101) = 80 -------- segundo 2*(10-2) = 0.02
tercero 4 * (102) = 400 -------- tercero 5*(10-3) = 0.005
cuarto 3 * (103) = 3000

10. Ejemplo de sistema de decimal

11. Sistema de numero hexadecimal
El sistema de numeración hexadecimal, o sea de base 16, (es común abreviar hexadecimal como hex
aunque hex significa base seis y no base dieciséis).
El sistema hexadecimal es compacto y nos proporciona un mecanismo sencillo de conversión hacia el
formato binario, debido a esto, la mayoría del equipo de cómputo actual utiliza el sistema numérico
hexadecimal.
Como la base del sistema hexadecimal es 16, cada dígito a la izquierda del punto hexadecimal
representa tantas veces un valor sucesivo potencia de 16, por ejemplo, el número 123416 es igual a:
1*163 + 2*162 + 3*161 + 4*160
lo que da como resultado:
4096 + 512 + 48 + 4 = 466010
Cada dígito hexadecimal puede representar uno de dieciséis valores entre 0 y 1510. Como sólo
tenemos diez dígitos decimales, necesitamos inventar seis dígitos adicionales para representar los
valores entre 1010 y 1510. En lugar de crear nuevos símbolos para estos dígitos, utilizamos las letras
A a la F.

12. Ejemplo de sistema numérico hexadecimal

13. Conversión de binario a decimal
Para poder transformar números binarios en su correspondiente decimal basta multiplicar el dígito
binario (que sólo puede ser 0 o 1) por 2 elevado a la potencia correspondiente según la cantidad de
dígitos de la cifra. Luego se suman los valores obtenidos y se consigue el número final.
Ejemplos
100011= 1*2^5 + 0*2^4 + 0*2^3 + 0*2^2 + 1*2^1 + 1*2^0 =
32 + 0 + 0 + 0 + 2 + 1 =
35
101= 1*2^2 + 0*2^1 + 1*2^0 =
4 + 0 + 1 =
5

14. Conversión de decimal a binario
Para convertir un número decimal a otro sistema, el número decimal es sucesivamente dividido por
la base del sistema. en este caso la base del sistema binario es 2 el número será sucesivamente
dividido entre 2 y el resultado del cociente será nuevamente dividido entre 2 y asi sucesivamente
hasta que el cociente sea 0. El resto de cada división es un número binario que conforma el número
resultante de la conversión. El primer resultado producido (el primer resto obtenido) corresponde al
bit mas próximo al punto decimal (o lo que se conoce como bit de menor peso). Los sucesivos bits
se colocan a la izquierda del anterior. No tese que esto es como escribir en sentido contrario al
empleado normalmente.
Ejemplos
20
20/2 = 10 Residuo = 0
10/2 = 5 Residuo = _0
5/2 = 2 Residuo = __1
2/2 = 1 Residuo = __0
1/2 = ? Residuo = __1
El 1 ya no se puede dividir entre 2 pero se coloca el 1
20 = 10100

15. Conversión de decimal a octal
En esta caso basta usar el mismo método de conversión con los números binarios. Pero en vez de hacer
divisiones sucesivas entre 2 hay que efectuarlas entre 8. Nótese que el divisor corresponde a la base del
sistema al cual se va a convertir.
Ejemplos
125 (Octal)
125/8 = 15 Residuo = 5
15/8 = 1 Residuo = __7
1/8 = 0 Residuo = ___1
125 (Octal) = 175 (Decimal)
175 (Octal)
175/8 = 21 Residuo = 7
21/8 = 2 Residuo = __5
2/8 = 0 Residuo = ___2
175 (Octal) = 257 (Decimal)

16. Conversión de hexadecimal A BINARIO
Para efectuar la conversión basta con colocar los cuatro bits correspondientes a cada símbolo del
número hexadecimal
Ejemplo
4B2 = 4 11 2
4 = 0100
11 = 1011
2 = 0010
4B2 = 0100 1011 0010

17. CONVERSION DE BINARIO A HEXADECIMAL
Para efectuar esta conversión hay que agrupar los bits de a cuatro comenzando con los primeros 4 bits de
la izquierda y siguiendo con los bits de la derecha
Ejemplos
011011010101 = 0110 1101 0101
0110 =____ 4
1101 = 13 = D
0101 =____ 5
0110 1101 0101 = 4D5
111101011001 = 1111 0101 1001
1111 = 15=_ F
0101 =____ 5
1010 = 10 = A
1111 0101 1001 = F5A

18. conclusión
El Sistema de Numeración es importante ya que con ellas nosotros cuantificamos las cosas
que generamos o que nos rodean, pero nosotros solo estamos acostumbrados a contar en
un sistema decimal, desde kínder nos enseñan los números decimales, nadie le pone
importancia a otro tipo de numeración, pero también es importante conocer otro tipo de
sistema de numeración, como lo son los binarios 0-1, el Octal, Hexadecimal. ya que estos
son sistemas reconocidos en programación, un ejemplo claro son los binarios ya que esta
numeración esta definida por el cero y el uno, esta numeración es importante aprenderla
por que al programar un sistema en una computadora solo reconoce sistemas binarios y no
los decimales, esto se debe a los contaste flujos de electricidad que le llega a un
computadora o algún otro aparato eléctrico programable.

19. infografía
https://es.wikipedia.org/wiki/Sistema_de_numeración_decimal
https://definicion.de/hexadecimal/