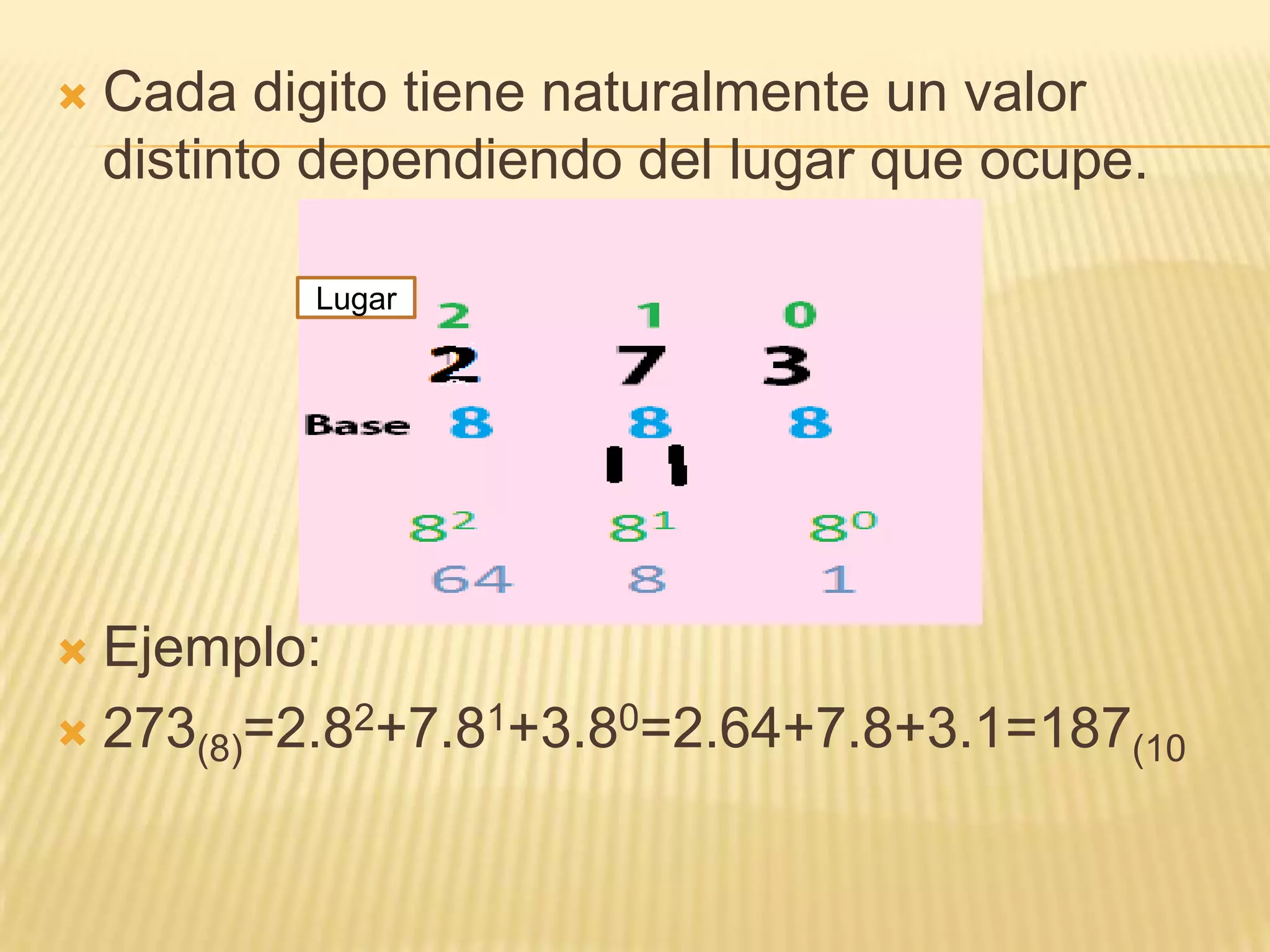
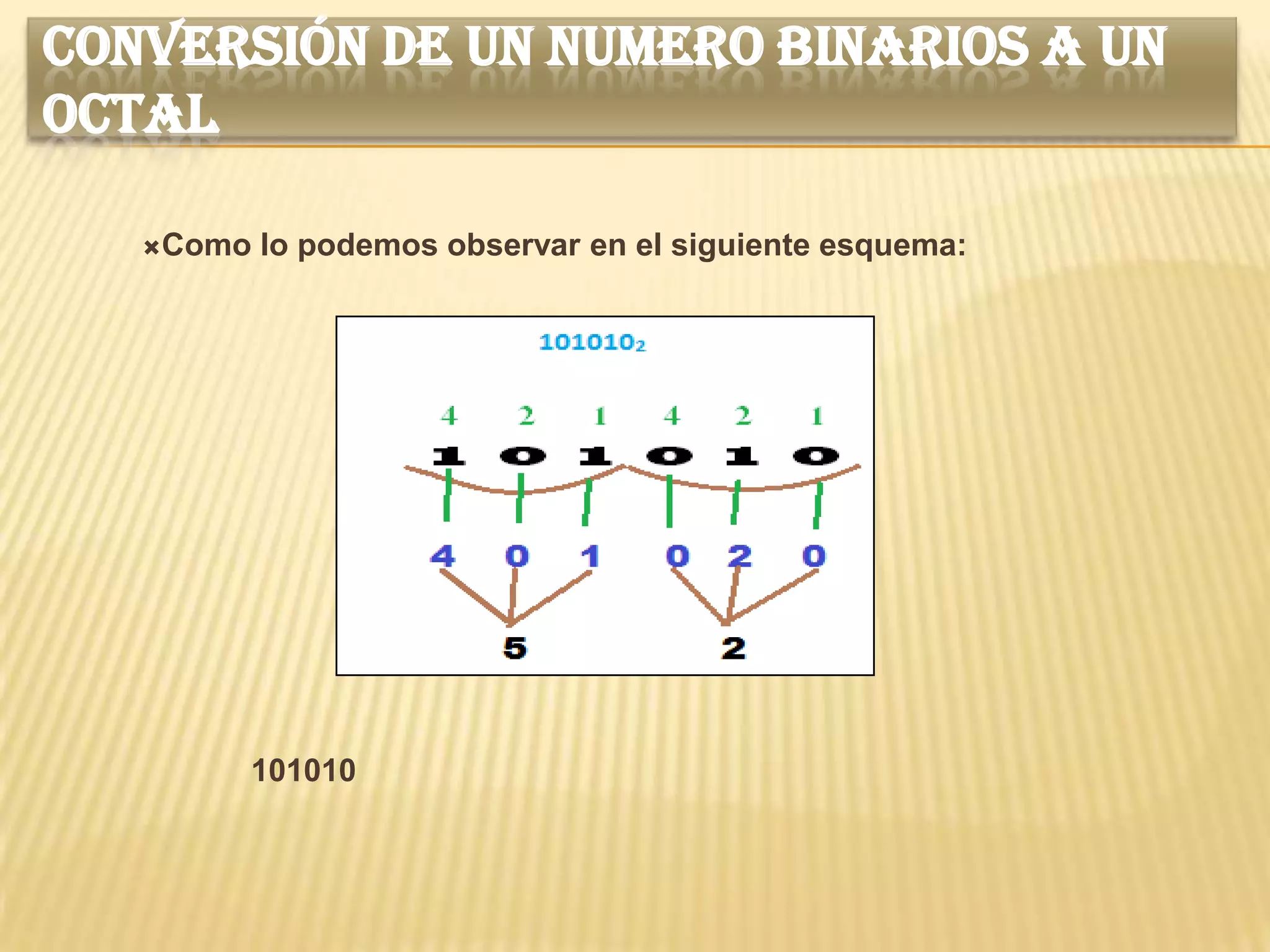
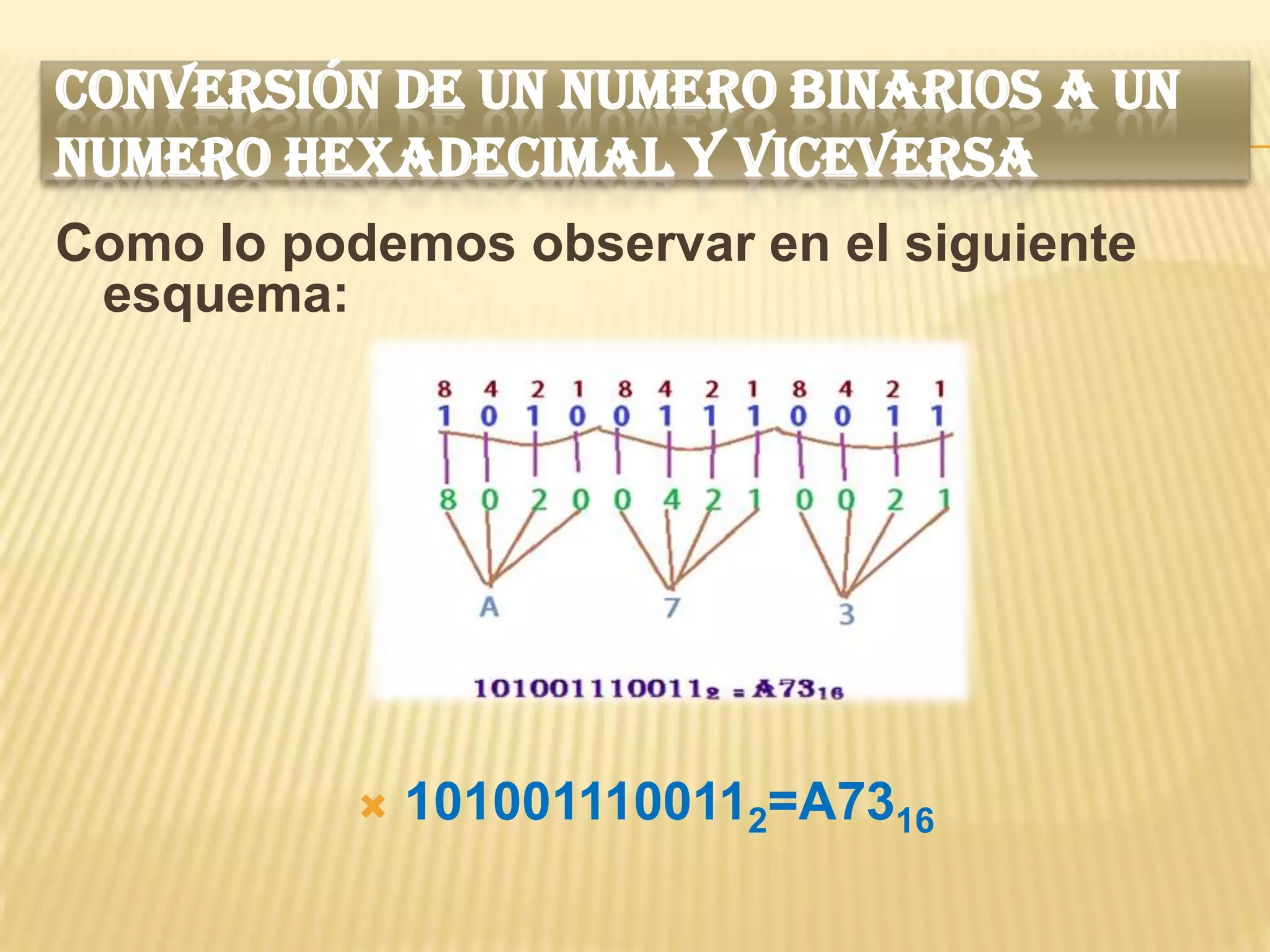
Este documento describe los diferentes sistemas de numeración como el decimal, binario, octal y hexadecimal. Explica que cada sistema se caracteriza por su base y los símbolos utilizados. También proporciona ejemplos de cómo convertir números entre los diferentes sistemas de numeración.

2. UNIVERSIDAD NACIONAL DE
CHIMBORAZO
FACULTAD CIENCIAS DE LA
EDUCACIÓN HUMANAS Y
TECNOLOGÍAS
ESCUELA DE INFORMATICA
APLICADA A LA EDUCACION

3. SISTEMAS DE NUMERACION
Lo podemos definir como un conjunto de símbolos y reglas de
generación que permiten construir todos los números válidos en el
sistema.
También es un Conjunto de Dígitos utilizados para representar
cantidades que se utilizan para la representación de datos
Numéricos o Cantidades.
Cada sistema de numeración se va ha caracterizar por su base que
es el número de cada símbolo distinto que utiliza, Y además
determina el valor de cada símbolo, dependiendo de la posición
que ocupe.

4. CLASIFICACION
Los Sistemas De Numeración Pueden Clasificarse En Dos Grandes
Grupos:
En Los Sistemas No-posicionales Los Dígitos Tienen El Valor Del Símbolo
Utilizado, Que No Depende De La Posición (Columna) Que Ocupan En El
Número.
Por Ejemplo El Sistema De Numeración Egipcio Es No Posicional es decir
que se permitía escribir grandes números y cantidades en fracciones
En Los Sistemas De Numeración Ponderados O Posicionales El Valor De
Un Dígito Depende Tanto Del Símbolo Utilizado, Como De La
Posición Que Ése Símbolo Ocupa En El Número.
Por Ejemplo El Babilónico Es Posicional. El digito 5 toma valores como
5,50,500

5. SISTEMA DECIMAL
 Sistema Decimal Su origen lo encontramos en la India y
fue introducido en España por los árabes. En el sistema
decimal los símbolos válidos para construir números son
{0,1,...9} (0 hasta 9, ambos incluidos), por tanto la base
el número de símbolos válidos en el sistema es diez.
 Su nombre proviene de los diez símbolos que usa y
también de los diez dedos de la mano del hombre.
 Ejemplo
 347= 3.100+4.10+7.1 o también 3.102+4.101+7.100

6. SISTEMA BINARIO
 El sistema binario trabaja de forma similar al sistema
decimal con dos diferencias, en este sistema los
dígitos válidos son {0,1}, y dos unidades forman una
unidad de orden superior.
 Su Basen es 2
 Proviene de dos vocablos Binary Digit
 El sistema binario es aquel que se utiliza en los
ordenadores o computadoras. Un número
binario cualquiera se puede representar, por
ejemplo, con las distintas posiciones de una
serie de interruptores.
 ‘Encendido' corresponde al 1,
 ‘Apagado' al 0.

7. SISTEMA OCTAL
 Su base es 8.
 Utiliza 8 dígitos : 0, 1, 2, 3, 4, 5, 6, 7
 El valor de cada una de las posiciones viene
determinado por la potencia y la base 8.

8.  Cada digito tiene naturalmente un valor
distinto dependiendo del lugar que ocupe.
Lugar
 Ejemplo:
 273(8)=2.82+7.81+3.80=2.64+7.8+3.1=187(10

9. SISTEMA HEXADECIMAL
 El sistema hexadecimal es compacto y nos proporciona un mecanismo
sencillo de conversión hacia el formato binario, debido a esto, la
mayoría del equipo de cómputo actual utiliza el sistema numérico
hexadecimal.
 Como la base del sistema hexadecimal es 16. Sus dígitos (0, 1, 2, 3, 4, 5, 6,
7, 8, 9, A, B, C, D, E, F). Se utilizan las letras (A,B,C,D,E,F) que
corresponden a los valores (10,11,12,13,14,15) Estos se utilizan porque
en el sistema decimal no hay valores mayores que 9.
 El valor de cada una de las posiciones viene determinado por la
potencia y la base.

10.  Cada digito tiene naturalmente un valor distinto dependiendo del
lugar que ocupe.
Lugar
 EJEMPLO DE SISTEMA EXADECIMAL: 1A3F
=1.163+A.162+3.161+F.160
=1.4096+10.256+3.16+15.1
=6719
 1A3F (16)=6719(10)

12. CONVERSIÓN DE UN NUMERO DECIMAL A BINARIO
 Transformemos el numero 42 a numero binario
 Para esta transformación es necesario tener en cuenta los pasos que
mostraremos a continuación:
1. Dividimos el numero 42 entre 2
2. Dividimos el cociente obtenido por 2 y repetimos el mismo procedimiento
hasta que el cociente sea 1.
3. El numero binario lo formamos tomando el primer dígito el ultimo cociente,
seguidos por los residuos obtenidos en cada división, seleccionándolos de
derecha a izquierda, como se muestra en el siguiente esquema.


13. CONVERSIÓN DE UN NUMERO DECIMAL A OCTAL
 Para convertir un numero en el sistema decimal al sistema de numeración
Octal, debemos seguir los pasos que mostraremos en el siguiente ejemplo
Convertir el numero decimal a el sistema de numeración Octal
Se toma el numero entero y se divide entre 8 repetidamente hasta que el
dividendo sea menor que el divisor, para colocar entonces el numero 0 y
pasar el dividendo a formar el primer dígito del numero equivalente en
decimal
 POR EJEMPLO 122(10)
 DIVIDIMOS

122(10)= 172(8)

14. CONVERSIÓN DE UN NUMERO DECIMAL A
HEXADECIMAL
 Para convertir un numero en el sistema decimal al sistema de numeración hexadecimal,
debemos seguir los pasos que mostraremos en el siguiente ejemplo Convertir el
numero decimal a el sistema de numeración hexadecimal
Se toma el numero entero y se divide entre 8 repetidamente hasta que el dividendo sea
menor que el divisor, para colocar entonces el numero 0 y pasar el dividendo a formar
el primer dígito del numero equivalente en decimal
 POR EJEMPLO 122(10)
 DIVIDIMOS

122(10)= 172(8)

15. CONVERSIÓN DE UN NUMERO BINARIO A UN NUMERO DECIMAL
 Para convertir un número binario a decimal, realizamos los
siguientes pasos:
1. Tomamos los valores de posición correspondiente a las
columnas donde aparezcan únicamente unos
2. Sumamos los valores de posición para identificar el numero
decimal equivalente

16. CONVERSIÓN DE UN NUMERO OCTAL A DECIMAL
 Es igualmente sencilla, conociendo el peso
de cada posición en una cifra octal
 Ejemplo:
 Para convertir el numero 237(8) a decimal
basta con desarrollar el valor de cada digito:
 2.82+3.81+7.80=128+24+7=159(10)
 237(8)=159(10)

17. CONVERSIÓN DE UN NUMERO HEXADECIMAL A UN
NUMERO DECIMAL
 Como en los ejemplos anteriores este también nos ayudará a
entender mejor este procedimiento: Convertir el numero
hexadecimal 2B6 a su equivalente decimal.
1. Multiplicamos el valor de posición de cada columna por el
dígito hexadecimal correspondiente.
2. El resultado del número decimal equivalente se obtiene,
sumando todos los productos obtenidos en el paso anterior.

18. CONVERSIÓN DE UN NUMERO BINARIOS A UN
OCTAL
 La conversión entre números hexadecimales y binarios
se realiza exponiendo o contrayendo cada digito
Hexadecimal a cuatro dígitos binarios.
 Por ejemplo
 Para expresar en Hexadecimal el numero
101001110011(2). Bastara como tomar grupo de cuatro
bits empezando siempre por la derecha y reemplazarlos
por su equivalente hexadecimal.
 10102=A8
 01112=78
 00112=38
 1010011100112=A738

19. CONVERSIÓN DE UN NUMERO BINARIOS A UN
OCTAL
Como lo podemos observar en el siguiente esquema:
101010

20. CONVERSIÓN DE UN NUMERO BINARIOS A UN
NUMERO HEXADECIMAL Y VICEVERSA
 La conversión entre números hexadecimales y binarios
se realiza exponiendo o contrayendo cada digito
Hexadecimal a cuatro dígitos binarios.
 Por ejemplo
 Para expresar en Hexadecimal el numero
101001110011(2). Bastara como tomar grupo de cuatro
bits empezando siempre por la derecha y reemplazarlos
por su equivalente hexadecimal.
 10102=A16
 01112=716
 00112=316
 1010011100112=A7316

21. CONVERSIÓN DE UN NUMERO BINARIOS A UN
NUMERO HEXADECIMAL Y VICEVERSA
Como lo podemos observar en el siguiente
esquema:
 1010011100112=A7316

22. CONVERSIÓN DE UN NUMERO OCTAL A BINARIO
 La ventaja principal del sistema de numeración Octal es
la facilidad conque pueden realizarse la conversión entre
un numero binario y octal.
 A continuación mostraremos un ejercicio que ilustrará la
teoría. Por medio de este tipo de conversiones,
cualquier numero Octal se convierte a binario de
manera individual.
 En este ejemplo, mostramos claramente el equivalente
100 111 010 en binario de cada numero octal de forma
individual.
