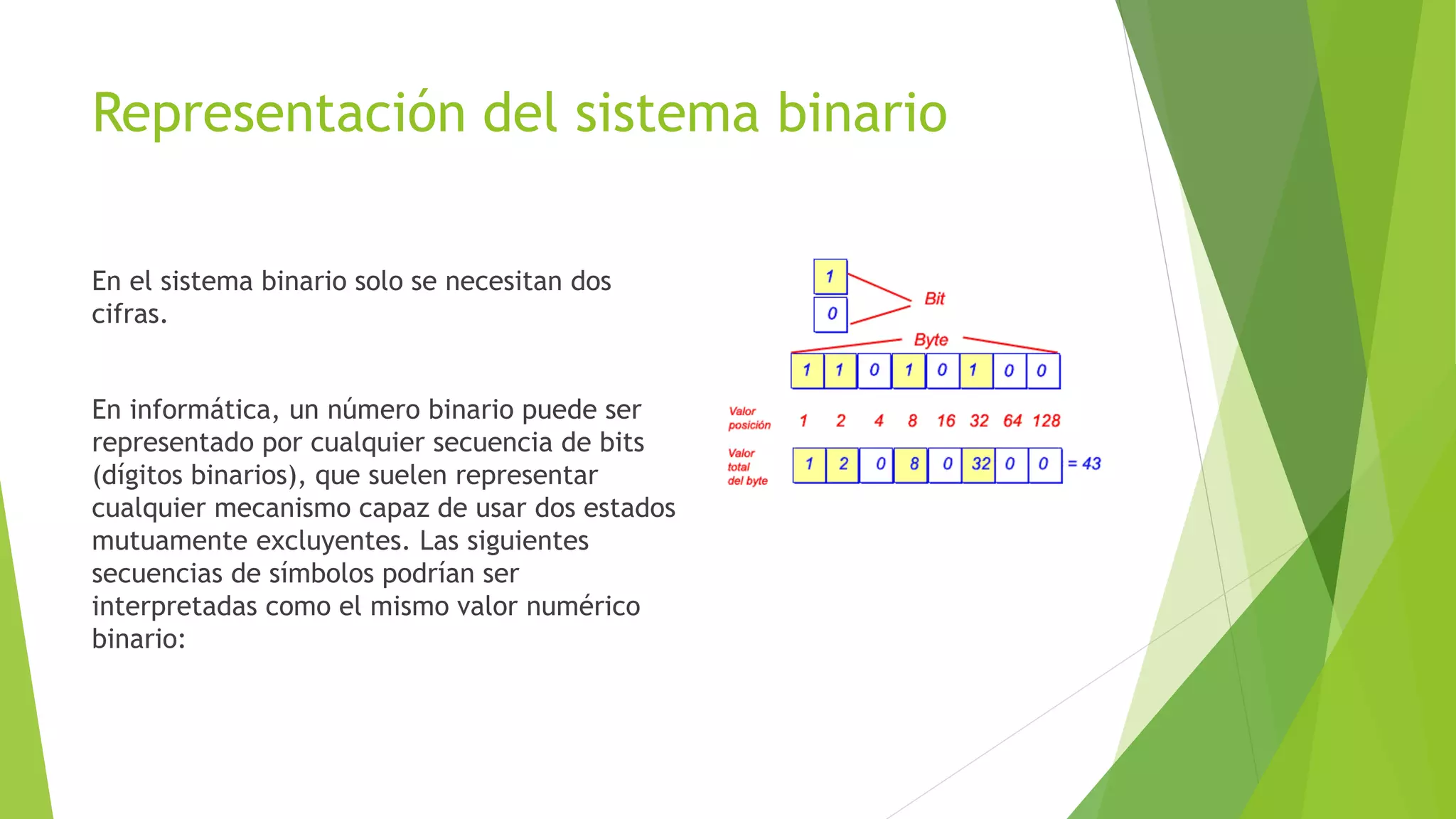
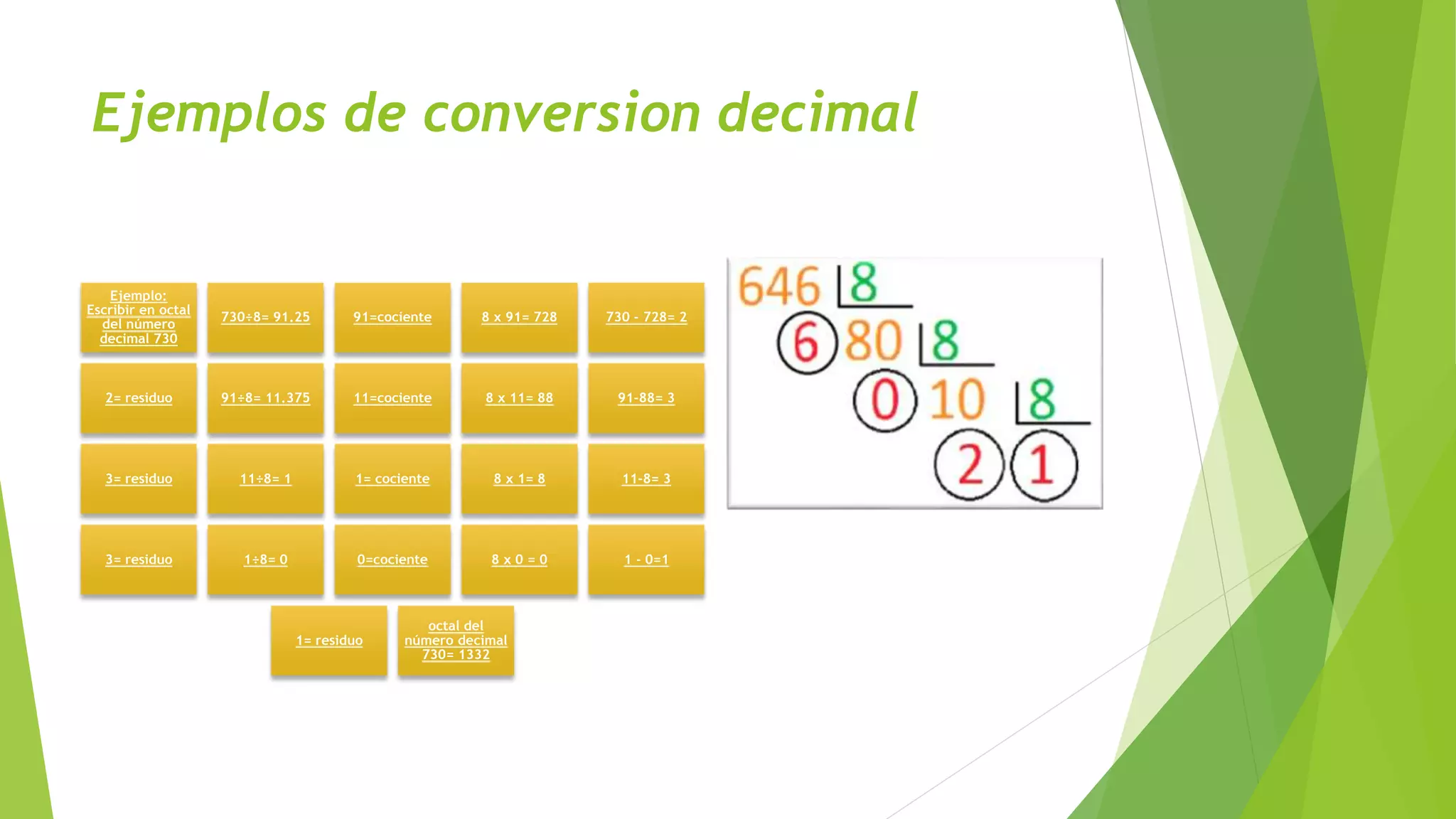
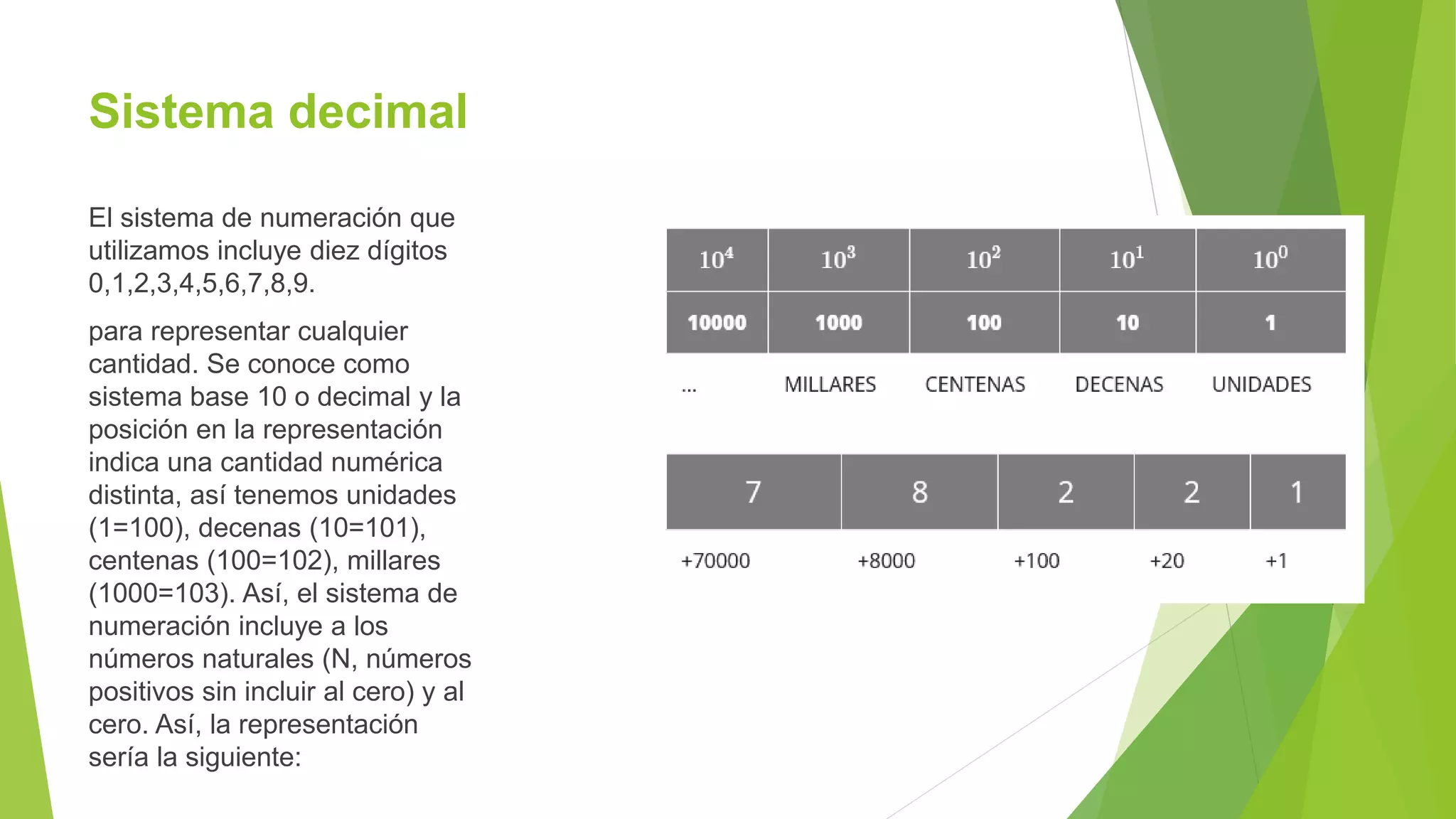
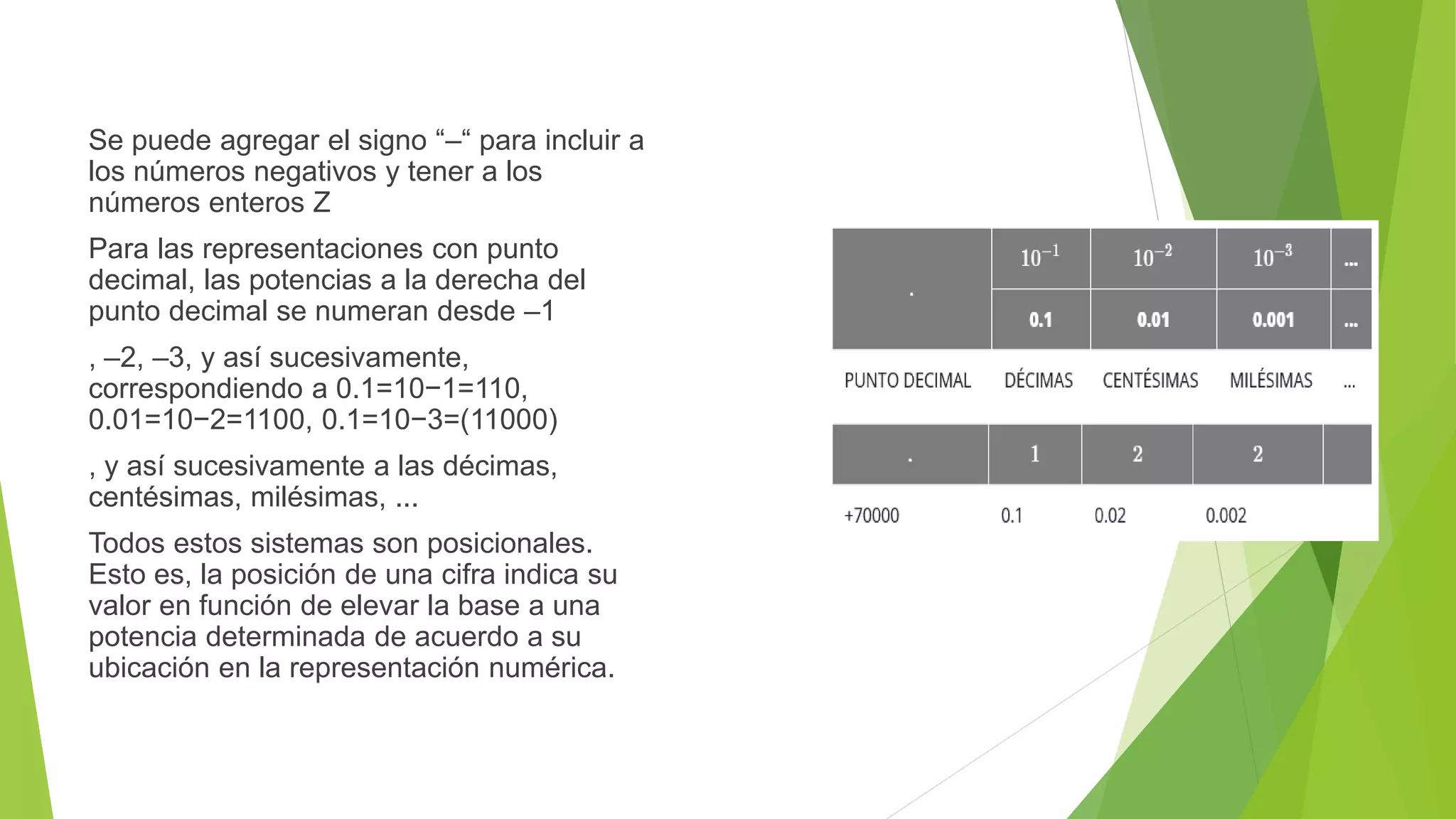
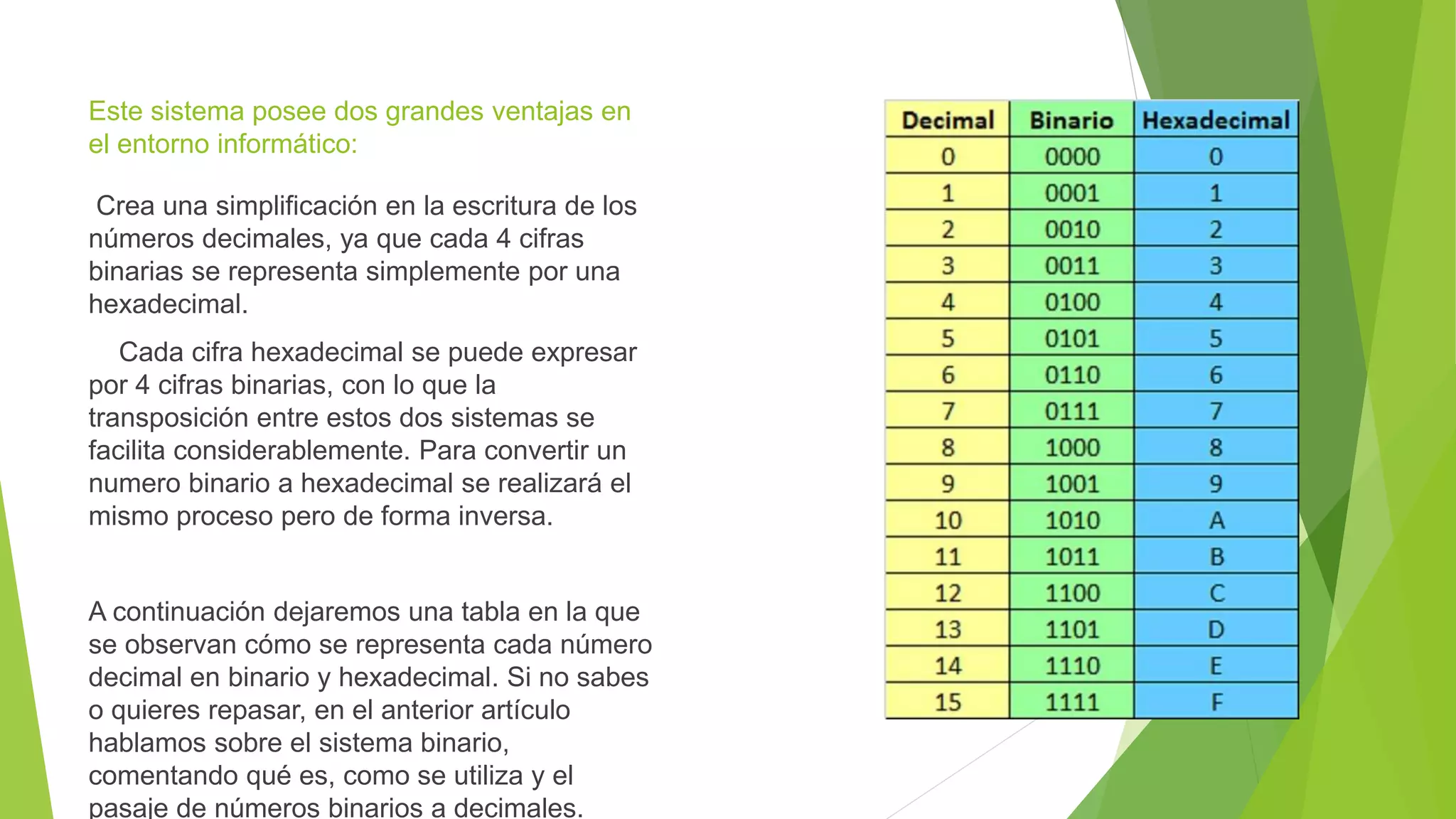
Este documento describe los principales sistemas numéricos utilizados en informática, incluyendo el binario, octal, decimal y hexadecimal. Explica cómo representar números en cada sistema y cómo convertir entre ellos, mediante divisiones sucesivas y agrupación de dígitos. Los sistemas numéricos son fundamentales para la representación de datos en computadoras y la comunicación entre sistemas digitales.

1. TEMA:SISTEMA
NUMERICO Y DE
CONVERSION
UNIVERCIDAD TECNOLOGICA DE PANAMA
PROFESORA: SUSAN OLIVA
INTEGRANTES:
ALMENGOR BRAYAN
CERRUD NADIA
ZAPATA JOSE

2. Índice
 Introducción
 Objetivos
 ¿Qué es un sistema numérico?
 El sistema binario
 Historia del sistema binario
 Aplicaciones del sistema binario.
 Aplicaciones del sistema binario.
 Representación del sistema binario
 Sistema numerico
Octal
 Sistema numerico octal
 Métodos de conversión

3.  Ejemplos de conversion decimal
 Ejemplo de Conversion binario a octal
 Sistema decimal
 Decimal a hexadecimal
 Sistema hexadecimal
 Este sistema posee dos grandes ventajas en el entorno informático:
 Hexadecimal a binario
 Hexadecimal a decimal
 Conclusión
 Infografía

4. Introducción
Los sistemas de numeración son las distintas formas de representar información numérica. Se
nombran haciendo referencia a la base, que representa al número de dígitos diferentes para
representar todos los números. El sistema habitual de numeración para las personas es el decimal,
cuya base es diez y corresponde a los distintos dedos de las mano, mientras que el método
habitualmente utilizados por los sistemas electrónicos digitales que utiliza solo 2 cifras para
representar la información que son: el 0 y el 1. Otros sistemas como el octal (base8) y el hexadecimal
(base 16) son utilizados con las computadoras.
Los sistemas de numeración son conjuntos de dígitos usados para representar cantidades, así se
tienen los sistemas de numeración decimal, binario, octal, hexadecimal; estos cuatro se caracterizan
por tener una base (número de dígitos diferentes: diez, dos, ocho, dieciséis respectivamente). Se
usan con el mismo fin, que es ofrecer un eficaz medio de representación de números binarios
grandes. Como veremos, ambos sistemas numéricos tienen la ventaja de que pueden convenirse
fácilmente al y del binario.

5. Objetivos
 Analizar y entender la importancia de los diferentes sistema numéricos y de conversión
que existen en la informática.
 Comprender de forma apropiada los usos y aplicaciones del sistema numérico y de
conversión.
 Reconocer e identificar las técnicas operativas y funcionales que ofrece el sistema
numérico y de conversión.
 Clasificar los diferentes sistemas numéricos y de conversión.

6. ¿Qué es un
sistema
numérico?
Un sistema de numeración es un conjunto
de símbolos y reglas que permiten
representar datos numéricos. Los sistemas
de numeración actuales son sistemas
posicionales, que se caracterizan porque
un símbolo tiene distinto valor según la
posición que ocupa en la cifra.

7. El sistema binario
Llamado también sistema diádico en
ciencias de la computación, es un
sistema de numeración en el que los
números son representados
utilizando únicamente dos cifras:
cero (0) y uno (1). Es uno de los
sistemas que se utilizan en las
computadoras, debido a que estas
trabajan internamente con dos
niveles de voltaje, por lo cual su
sistema de numeración natural es el
sistema binario.

8. Historia del sistema binario
El antiguo matemático hindú Pingala presentó la
primera descripción que se conoce de un
sistema de numeración binario en el siglo
tercero antes de nuestra era, lo cual coincidió
con su descubrimiento del concepto del número
cero.
El erudito y filósofo chino Shao Yong en el siglo
XI desarrolló un arreglo binario ordenado de los
hexagramas del I Ching, representando la
secuencia decimal de 0 a 63, y un método para
generar el mismo.

9. Aplicaciones del sistema binario.
 En 1937, Claude Shannon realizó su tesis
doctoral en el MIT, en la cual implantaba el
Álgebra de Boole y la aritmética binaria
utilizando relés y conmutadores por primera
vez en la historia. Titulada Un Análisis
Simbólico de Circuitos Conmutadores y Relés,
la tesis de Shannon básicamente fundó el
diseño práctico de circuitos digitales.

10. Aplicaciones del sistema binario.
En noviembre de 1937, George Stibitz,
trabajando por aquel entonces en los
Laboratorios Bell, construyó una calculadora
basada en relés —a la cual apodó "Modelo K"
(porque la construyó en una cocina, en inglés
"kitchen")— que utilizaba la suma binaria para
realizar los cálculos. Los Laboratorios Bell
autorizaron un completo programa de
investigación a finales de 1938, con Stibitz al
mando.

11. Representación del sistema binario
En el sistema binario solo se necesitan dos
cifras.
En informática, un número binario puede ser
representado por cualquier secuencia de bits
(dígitos binarios), que suelen representar
cualquier mecanismo capaz de usar dos estados
mutuamente excluyentes. Las siguientes
secuencias de símbolos podrían ser
interpretadas como el mismo valor numérico
binario:

12. Sistema
numerico
Octal

13. Sistema
numerico octal
 El sistema de numeración posicional cuya
base es 8, se llama octal y utiliza los dígitos
indio arábigos: 0,1,2,3,4,5,6,7. En
informática a veces se utiliza la numeración
octal en vez de la hexadecimal. Tiene la
ventaja de que no requiere utilizar otros
símbolos diferentes de los dígitos. Sin
embargo, para trabajar con bytes o
conjuntos de ellos, asumiendo que un byte
es una palabra de 8 bits, suele ser más
cómodo el sistema hexadecimal, por cuanto
todo byte así definido es completamente
representable por dos dígitos
hexadecimales.

14. Métodos de conversión
Decimal a Octal
 Para poder convertir un número en
base decimal a base octal se divide
dicho número entre 8, dejando el
residuo y dividiendo el cociente
sucesivamente entre 8 hasta obtener
cociente 0, luego los restos de las
divisiones leídos en orden inverso
indican el número en octal.
BINARIO A Octal
 Para pasar de binario a octal, solo hay
que agrupar de 3 en 3 los dígitos
binarios, así, el número binario
1001010 (74 en decimal), lo
agruparíamos como 1 / 001 / 010.

15. Ejemplos de conversion decimal
Ejemplo:
Escribir en octal
del número
decimal 730
730÷8= 91.25 91=cociente 8 x 91= 728 730 - 728= 2
2= residuo 91÷8= 11.375 11=cociente 8 x 11= 88 91-88= 3
3= residuo 11÷8= 1 1= cociente 8 x 1= 8 11-8= 3
3= residuo 1÷8= 0 0=cociente 8 x 0 = 0 1 - 0=1
1= residuo
octal del
número decimal
730= 1332

16. Ejemplo de
Conversion
binario a octal
 Por ejemplo, tendrías
que separar el
número binario 101001
en 101 001. Agrega ceros
a la izquierda del último
dígito, si no tienes
suficientes dígitos para
formar el último grupo
de tres. El
número binario 10011011
tiene ocho dígitos, y a
pesar de no ser múltiplo
de tres, igual puedes
convertirlo en octal.

17. Sistema decimal
El sistema de numeración que
utilizamos incluye diez dígitos
0,1,2,3,4,5,6,7,8,9.
para representar cualquier
cantidad. Se conoce como
sistema base 10 o decimal y la
posición en la representación
indica una cantidad numérica
distinta, así tenemos unidades
(1=100), decenas (10=101),
centenas (100=102), millares
(1000=103). Así, el sistema de
numeración incluye a los
números naturales (N, números
positivos sin incluir al cero) y al
cero. Así, la representación
sería la siguiente:

18. El número 78,221 incluye los dígitos
1,2,7,8 que están incluidos o
pertenecen a los dígitos decimales
0,1,2,3,4,5,6,7,8,9. Hay que notar
que el dígito 2 aparece dos veces
en este número, pero por la
posición que ocupan, la primera
ocurrencia vale 200(2×102) y la
segunda aparición vale 20(2×103)
Observa la siguiente animación
para que recuerdes cómo funciona
un sistema posicional. No olvides
que hacia el lado derecho del punto
decimal los exponentes
incrementan de derecha a
izquierda. Desde el punto decimal,
la primera posición comienza a
numerarse desde cero, esta
posición corresponde a las
unidades en cualquier sistema de
numeración.

19. El número 78,221 incluye los dígitos
1,2,7,8 que están incluidos o
pertenecen a los dígitos decimales
0,1,2,3,4,5,6,7,8,9. Hay que notar
que el dígito 2 aparece dos veces
en este número, pero por la
posición que ocupan, la primera
ocurrencia vale 200(2×102) y la
segunda aparición vale 20(2×103)
Observa la siguiente animación
para que recuerdes cómo funciona
un sistema posicional. No olvides
que hacia el lado derecho del punto
decimal los exponentes
incrementan de derecha a
izquierda. Desde el punto decimal,
la primera posición comienza a
numerarse desde cero, esta
posición corresponde a las
unidades en cualquier sistema de
numeración.

20. Se puede agregar el signo “–“ para incluir a
los números negativos y tener a los
números enteros Z
Para las representaciones con punto
decimal, las potencias a la derecha del
punto decimal se numeran desde –1
, –2, –3, y así sucesivamente,
correspondiendo a 0.1=10−1=110,
0.01=10−2=1100, 0.1=10−3=(11000)
, y así sucesivamente a las décimas,
centésimas, milésimas, ...
Todos estos sistemas son posicionales.
Esto es, la posición de una cifra indica su
valor en función de elevar la base a una
potencia determinada de acuerdo a su
ubicación en la representación numérica.

21. Decimal a
hexadecimal
Queremos convertir el número decimal 350 a
hexadecimal
Cómo vemos en la imagen:
350 dividido entre 16 da como cociente 21 y
resto 14
21 dividido entre 16 da como cociente 1 y resto
5
Cómo dijimos antes, primero se toma el cociente
final (1) y luego los restos de forma sucesiva de
atrás para adelante (5 y 14). Recordando que 14
= E.
Por lo tanto 350 decimal = 15E hexadecimal.

22. Sistema hexadecimal
El sistema hexadecimal es el sistema de numeración posicional que tiene como
base el 16. Sus números están representados por los 10 primeros dígitos de la
numeración decimal, y el intervalo que va del número 10 al 15 están
representados por las letras del alfabeto de la ‘A’ a la ‘F’.
Su uso actual está muy vinculado a la informática y ciencias de la computación
donde las operaciones de la CPU suelen usar el byte u octeto como unidad básica
de memoria. Aunque los circuitos electrónicos digitales y las computadoras utilizan
el sistema binario, el trabajar con este sistema de numeración es bastante más
complicado, lo que da como resultado una gran posibilidad de cometer errores se
trabaja con números binarios demasiado largos.

23. Este sistema posee dos grandes ventajas en
el entorno informático:
Crea una simplificación en la escritura de los
números decimales, ya que cada 4 cifras
binarias se representa simplemente por una
hexadecimal.
Cada cifra hexadecimal se puede expresar
por 4 cifras binarias, con lo que la
transposición entre estos dos sistemas se
facilita considerablemente. Para convertir un
numero binario a hexadecimal se realizará el
mismo proceso pero de forma inversa.
A continuación dejaremos una tabla en la que
se observan cómo se representa cada número
decimal en binario y hexadecimal. Si no sabes
o quieres repasar, en el anterior artículo
hablamos sobre el sistema binario,
comentando qué es, como se utiliza y el
pasaje de números binarios a decimales.

24. Hexadecimal a binario
Queremos convertir el número hexadecimal A6D16 a binario. Cómo vimos en la tabla de arriba
podemos sacar los datos necesarios:
A = 1010
6 = 0110
D = 1101
Por lo tanto A6D16 = 1010 0110 1101
Para pasar un número hexadecimal a un número decimal, debemos de multiplicar los números
hexadecimales por las distintas potencias de la base 16 que representa cada digito del sistema
hexadecimal.

25. Hexadecimal a decimal
Veremos convertir el número hexadecimal A6D16 a decimal:
A6D = 10×162 + 6×161 + 13×160 = 2560 + 96 + 13 = 2669
Por lo tanto A6D16 = 2669
De forma contraria se obtendrán la conversión de número decimal a hexadecimal. Debemos
de dividir por 16 sucesivamente hasta no poder realizarlo más. El número resultante estará
constituido por el último cociente seguido de todos los restos.

26. Conclusión
Los sistemas de numeración son conjuntos de símbolos y reglas que representan
datos numéricos, son usados como sistemas posicionales, de esta manera,
dependiendo la posición que ocupa en la fila, cada símbolo tendrá un valor diferente.
Para realizar las conversiones bastará con realizar divisiones, en el caso de números
decimales, tomando el resto como el valor final. En el caso de los números binarios
únicamente se necesita separar los bits y encontrar el número equivalente. Como no
existe una manera directa de convertir de hexadecimal a octal y viceversa, es
necesario convertir a binario y posteriormente de binario al sistema numérico deseado.
Las comprobaciones también resultan sencillas, pues bastará con realizar la
conversión al revés o usando la tabla de conversiones del sistema numérico para cada
una de las expresiones a convertir. Definitivamente los sistemas numéricos son y
forman una parte fundamental de los sistemas digitales de la actualidad, comprender y
entender las diferentes conversiones entre estos sistemas numéricos es muy
importante para nuestra carrera como en Desarrollo de Software, ya que son una
pieza fundamental en la comunicación hombre- máquina en el sector informático y
digital.

27. Infografía
- https://www.areatecnologia.com/sistema-binario.htm
- https://blogs.ua.es/.../sistemas-de-numeracion/sistema-de-numeracion-octal
- https://www.recursos.feyalegria.edu.pe/el-sistema-numerico-decimal..
- https://www.euston96.com/sistema-hexadecimal