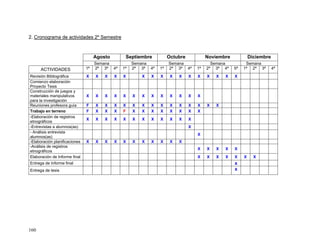
La investigación busca determinar si los juegos educativos y materiales manipulativos influyen en la disposición para el aprendizaje de las matemáticas en alumnos y alumnas de cuarto año básico de un colegio particular subvencionado de Temuco. Se implementó una metodología basada en juegos y materiales manipulativos durante cinco meses, aplicando instrumentos como cuestionarios inicial y final, entrevistas y observaciones. Los resultados del cuestionario final mostraron un cambio en la disposición de los estudiantes luego de trabajar