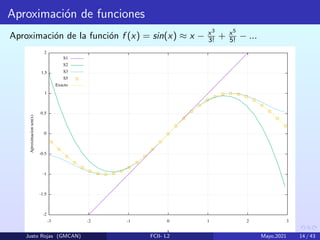
Este documento trata sobre los errores de cálculo en las computadoras. Existen dos tipos principales de errores: (1) el error de truncamiento, que ocurre cuando se aproxima un proceso infinito con uno finito, y (2) el error de redondeo, que surge debido a la representación limitada de números reales en las computadoras. El documento analiza estas fuentes de error y cómo identificar y minimizar los errores en los problemas computacionales.














![Teorema de Taylor
Teorema de Taylor
Si la función f (x) tiene derivadas continuas de ordenes hasta (n+1) en el
intervalo cerrado I=[a-b], entonces para cualquier a y x en I,
f (x) =
n
X
k=0
f (k)(a)
k!
(x − a)k
+ En+1 (4)
donde el término resto En+1 puede estar dado en la forma
En+1 =
f (n+1)(ξ)
(n + 1)!
(x − a)n+1
(5)
aqui ξ es un punto que se encuentra entre a y x.
Justo Rojas (GMCAN) FCII- L2 Mayo,2021 12 / 43](https://image.slidesharecdn.com/l2errores-210608161553/85/L2-errores-15-320.jpg)