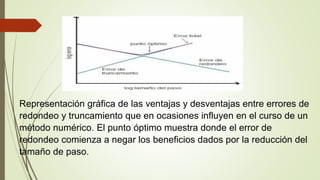
Este documento resume los conceptos fundamentales del análisis numérico, incluyendo diferentes tipos de errores como errores de truncamiento, redondeo y formulación. También describe cómo los métodos numéricos permiten aproximar soluciones a problemas del mundo real utilizando operaciones aritméticas básicas en un computador.

1. ALUMNO: NIEL VELASQUEZ
V- 10.382.323
INTRODUCCION AL
ANALISIS NUMERICO
Y
TEORIA DE
ERRORES
UNIVERSIDAD: "FERMÍN TORO"
DECANATO DE INGENIERÍA
ESCUELA DE INGENIERÍA ELECTRICA
ASIGNATURA: ANALISIS NUMERICO
SECCIÓN B
TUTOR: DOMINGO MENDEZ

2. INTRODUCCION.
En el presente trabajo nos adentraremos en el
mundo del análisis numérico o también llamado
método numérico se analizaran los diferentes
conceptos de esta rama de la ciencia matemática,
además de definir el Error y sus diferentes formas

3. La mayoría de los problemas a los que se enfrenta el ingeniero
son de naturaleza continua. En la búsqueda de su solución no es
fácil disponer de métodos analíticos o exactos, que permitan
el análisis, validación y verificación de los modelos, tanto
matemáticos como computacionales, que los representan.
Además, casi todos estos modelos involucran temas como
derivación, integración, sistemas de ecuaciones no lineales,
sistemas de ecuaciones diferenciales, etc., cuya solución implica
la utilización de procesos iterativos que generalmente no se
pueden resolver en un número finito de pasos.
ANALISIS NUMERICO

4. Son una opción importante que ayuda a enfrentar y resolver los
problemas del mundo real. Estos métodos son técnicas que
permiten resolver problemas utilizando simples operaciones
aritméticas (+, -, * y /) por medio de su principal herramienta: el
computador digital. Se caracterizan por la cantidad de cálculos
repetitivos que deben realizarse para finalmente converger a una
solución lo suficientemente aproximada "o cercana" del problema;
por esta razón, es fundamental conocer las ventajas y limitaciones,
de los diferentes métodos, en relación a temas
como error, exactitud, precisión, estabilidad, a fin de utilizar el
método más apropiado en cada situación particular.
ANALISIS NUMERICO

5. El desarrollo que ha tenido en los últimos años el
computador digital, ha influido de manera significativa
no solo en la evolución y perfeccionamiento de estos
métodos, sino además, en la elaboración y solución de
modelos cada vez más complejos, los cuales permiten
responder satisfactoriamente a preguntas relacionadas
con temas como seguridad, salud, medio ambiente,
desarrollo y crecimiento social entre otros
ANALISIS NUMERICO

6. El análisis numérico o calculo numérico es la rama de
las matemáticas encargada de diseñar algoritmos para
a través de números y reglas matemáticas simples,
simular procesos matemáticos mas complejos
aplicados a procesos del mundo real.
El análisis numérico o cálculo numérico

7. El análisis numérico cobra especial cobra
especial importancia con la llegada de los
ordenadores. Los ordenadores son útiles
para cálculos matemáticos extremadamente
complejos, pero en ultima instancia operan
con números binarios y operaciones
matemáticas simples

8. Desde este punto de vista, el análisis numérico
proporcionará todo el andamiaje necesario para
llevar a cabo todos aquellos procedimientos
matemáticos susceptibles de expresarse
algorítmicamente, basándose en algoritmos que
permitan su simulación o cálculo en procesos más
sencillos empleando números. Definido el error,
junto con el error admisible, pasamos al concepto
de estabilidad de los algoritmos. Muchas de las
operaciones matemáticas

9. pueden llevarse adelante a través de la
generación de una serie de números que a su
vez alimentan de nuevo el algoritmo (feedback).
Esto proporciona un poder de cálculo y
refinamiento importantísimo a la máquina que a
medida que va completando un ciclo va llegando
a la solución. El problema ocurre en determinar
hasta cuándo deberá continuar con el ciclo, o si
nos estamos alejando de la solución del
problema.

10. Finalmente, otro concepto paralelo al análisis numérico es
el de la representación, tanto de los números como de
otros conceptos matemáticos como los vectores,
polinomios , etc. Por ejemplo, para la representación en
ordenadores de números reales, se emplea el concepto
de coma flotante que dista mucho del empleado por la
matemática convencional.

11. Enumerare algunas de las aplicaciones del análisis
numérico;
 Astrodinámica: cálculo de trayectoria de los satélites
 La mecánica celeste: estudia el movimiento de los
astro considerando las perturbaciones creadas por sus
vecinos
 La astrofísica: modelando de la evolución de las
estrellas
 La ingeniería civil Estudio de las características
estructurales de grandes estructural. (edificios,
puentes, prensas.)
 La meteorología: predicciones del tiempo, Cambio
climático
 La biología dinámica de poblaciones.
 Flujo de sangre en el cuerpo humano
 Mecánica de fluido: simulación de flujo de aire de una
nave y las correspondientes presiones sobre la
estructura.
 Disipación de contaminantes en diferentes medios.

12. Los errores numéricos se generan con el uso de
aproximaciones para representar las operaciones y
cantidades matemáticas. La relación entre el
resultado exacto o verdadero y el aproximado está
dada por:
Valor verdadero = aproximación + error
De lo anterior se concluye que el error numérico
resulta de la diferencia entre el valor verdadero y la
aproximación,
Ev = valor verdadero – aproximación
Ev : Valor “exacto” o “verdadero” del error.
No siempre se cuenta con el valor verdadero, por lo
que se debe emplear una estimación “aproximada”
del error. Esta definición no toma en cuenta la
magnitud de la medición.
Ej.: Un error de 1 cm. es mucho más significativo si
se está midiendo una hoja tamaño carta, que un
puente.
Una manera de tener en cuenta la magnitud es
normalizar el error respecto a un valor de referencia, a
esta nueva forma de redefinir el error se le llama Error
Relativo:
DEFINICION DE ERROR
NUMERICO

13. TIPO DE ERRORES NUMERICOS
En todo sistema de cómputos los métodos numéricos
no son negados a tener situaciones de error . Las
mismas son denominadas errores numéricos y podemos
enumerar dos tipos de errores los cuales son:
• Errores Absolutos
• Errores Relativos
• Errores de Truncamiento
• Errores de Redondeo
• Errores de Suma y Resta

14. Tipos de Errores
Los errores numéricos se generan con el uso de aproximaciones
para representar las operaciones y cantidades matemáticas. Estos
incluyen de truncamiento que resultan de representar
aproximadamente un procedimiento matemático exacto, y los
errores de redondeo, que resultan de presentar aproximadamente
números exactos. Para los tipos de errores, la relación entre el
resultado exacto o verdadero y el aproximado está dado por:
E = P* - P
Bien sea una medida directa (la que da el aparato) o indirecta
(utilizando una fórmula) existe un tratamiento de los errores de
medida. Podemos distinguir dos tipos de errores que se utilizan
en los cálculos.

15.  Error relativo.
Es el cociente (la división) entre el error absoluto
y el valor exacto. Si se multiplica por 100 se
obtiene el tanto por ciento (%) de error. Al igual
que el error absoluto puede ser positivo o negativo
(según lo sea el error absoluto) porque puede ser
por exceso o por defecto. no tiene unidades.
Y el error relativo como
ER = | P* - P| / P , si P =/ 0
El error relativo también se puede multiplicar por
el 100% para expresarlo como:
ERP = ER x 100

16. ERRORES DE REDONDEO
Los errores de redondeo se deben a que las
computadoras solo guardan un número finito de cifras
significativas durante un cálculo. Las computadoras
realizan esta función de maneras diferentes; esta
técnica de retener solo los primeros siete términos se
llamaron “truncamiento” en el ambiente de computación.
De preferencia se llamara de corte, para distinguirlo de
los errores de truncamiento. Un corte ignora los
términos restantes de la representación decimal
completa

17. La mayor parte de las computadoras tienen entre 7 y 14 cifras
significativas, los errores de redondeo parecerían no ser muy
importantes. Sin embargo, hay dos razones del por qué pueden
resultar críticos en algunos métodos numéricos:
1) Ciertos métodos requieren cantidades extremadamente grandes
para obtener una respuesta. Además, estos cálculos a menudo
dependen entre si, es decir, los cálculos posteriores son dependientes
de los anteriores. En consecuencia, aunque un error de redondeo
individual puede ser muy pequeño, el efecto de acumulación en el
transcurso de la gran cantidad de cálculos puede ser significativo.

18. 2) El efecto de redondeo puede ser exagerado cuando se llevan
a cabo operaciones algebraicas que emplean números muy
pequeños y muy grandes al mismo tiempo. Ya que este caso se
presenta en muchos métodos numéricos, el error de redondeo
puede resultar de mucha importancia.

19. ERRORES DE TRUNCAMIENTO
Los errores de truncamiento son aquellos que resultan
al usar una aproximación en lugar de un procedimiento
matemático exacto.
Estos tipos de errores son evaluados con una
formulación matemática: la serie de Taylor.
Taylor es una formulación para predecir el valor de la
función en Xi+1 en términos de la función y de sus
derivadas en una vecindad del punto Xi.
Siendo el termino final:
Rn= ((ƒ(n+1) (ξ))/(n+1)!)hn+1

20. En general, la expansión en serie de Taylor de
n-ésimo orden es exacta par aunpolinomio de
n-ésimo orden. Para otras funciones continuas
diferenciables, como las exponenciales o
senoidales, no se obtiene una estimación exacta
mediante un número finito de términos. Cada una
de los términos adicionales contribuye al
mejoramiento de la aproximación, aunque sea un
poco.

21. ERROR NUMERICO TOTAL
El error numérico total es la suma de los errores de redondeo y de
truncamiento. La única forma de minimizar los errores de redondeo
es la de incrementar el número de cifras significativas de la
computadora.

22. Representación gráfica de las ventajas y desventajas entre errores de
redondeo y truncamiento que en ocasiones influyen en el curso de un
método numérico. El punto óptimo muestra donde el error de
redondeo comienza a negar los beneficios dados por la reducción del
tamaño de paso.

23. ERRORES POR EQUIVOCACIÓN
En los primeros años de la computación los resultados numéricos
erróneos fueron atribuidos algunas veces al mal funcionamiento de la
computadora misma. Hoy día esta fuente de error es muy improbable
y la mayor parte de las equivocaciones se atribuye a errores
humanos.
Las equivocaciones ocurren a cualquier nivel del proceso de
modelación matemática y pueden contribuir con todas las otras
componentes del error. Las equivocaciones, por lo general se pasan
por alto en la discusión del método numérico. Esto sin duda prueba
el hecho de que los errores de torpeza son, hasta cierto punto
inevitables.

24. ERRORES DE FORMULACIÓN
Los errores de formulación o de modelamiento degeneran en
lo que se podría considerar como un modelo matemático
incompleto, ya que si se está usando un modelo deficiente,
ningún método numérico generara los resultados adecuados.

25. CONCLUSION
El análisis numérico es el desarrollo y estudio de
procedimientos para resolver problemas con ayuda
de una computadora. El termino algoritmo se emplea
para designar un procedimiento sistemático que
resuelve un problema

26. BIBLOGRAFIA
ANALISIS NUMERICO CON APLICACIONES
SEXTA EDICION
CURTIS F. GERARD
PATRICK O.WHEATLEY
TRADUCIDO POR:
HUGO VILLAGOMEZ VELASQUEZ
PEARSON
PRETICE HALL