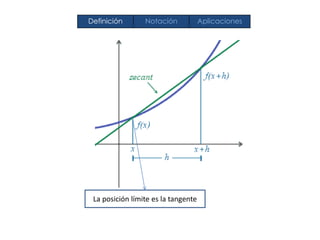
El documento resume la definición, notación y aplicaciones de la derivada. Define la derivada como el límite de la pendiente de las rectas secantes que se aproximan a la tangente. Explica que la notación más común usa un apóstrofe para indicar la derivada y que las aplicaciones incluyen calcular la recta tangente, graficar funciones y su uso en física.

1. La Derivada
Universidad de Cuenca
Facultad de Ingeniería
Ing. Esteban Sánchez Cordero M.sc

2. Estructura de la presentación
Definición Notación Aplicaciones
• Definición
• Notación
• Aplicaciones

3. Definición
Las derivadas se definen tomando el límite de la
pendiente de las rectas secantes conforme se van
aproximando a la recta tangente.
Cuando tomemos el límite de las pendientes de las
secantes próximas, obtendremos la pendiente de la
recta tangente
Definición Notación Aplicaciones

4. La derivada de f en x es el límite del valor del
cociente diferencial conforme las líneas secantes se
acercan más a la tangente:
Definición Notación Aplicaciones

5. Definición Notación Aplicaciones
La posición límite es la tangente

6. Notación
La notación más simple para la diferenciación que se
utiliza en la actualidad se debe a Lagrange y utiliza
un apóstrofo o comilla: ′
Definición Notación Aplicaciones

7. De esta manera se expresan las derivadas de la
función f(x) en el punto x = a, se escribe:
para la primera derivada,
para la segunda derivada,
para la tercera derivada,
para la n-ésima derivada (donde normalmente
se da que n > 3).
Definición Notación Aplicaciones

8. La otra notación común para la diferenciación se
debe a Leibniz
Definición Notación Aplicaciones

9. La notación de Newton para la diferenciación
consiste en poner un punto sobre el nombre
de la función:
Definición Notación Aplicaciones

10. Aplicaciones
 Recta tangente a una función en un punto
 Uso de las derivadas para realizar gráficos de
funciones
 Física
Definición Notación Aplicaciones

11. GRACIAS
Tomado de: http://es.wikipedia.org/wiki/C%C3%A1lculo_diferencial