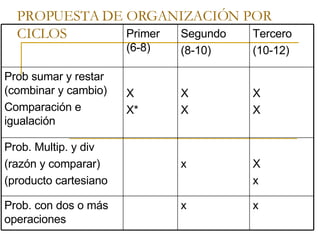
El documento aborda la importancia de la resolución de problemas en la enseñanza de las matemáticas, destacando su papel como justificación, motivación y vehículo de aprendizaje. Se identifican dificultades comunes que enfrentan los alumnos, estrategias de resolución y se presentan diferentes tipos de problemas, incluyendo aritméticos, aditivos y multiplicativos. Además, se proponen métodos de enseñanza que integran la planificación y gestión de recursos para mejorar la competencia matemática y la capacidad de los estudiantes para abordar problemas en contextos reales.

1. Proyecto La enseñanza activa de las Matemáticas Módulo: RESOLUCIÓN DE PROBLEMAS Las Palmas de Gran Canaria 15 de enero de 2008

2. La resolución de problemas "La resolución de problemas debe ser el eje de la enseñanza de las matemáticas" Agenda in action, 1980

3. ¿ Cuál crees que es el papel que juega la resolución de problemas en la enseñanza actual y cuál debería ser? A) Como justificación para enseñar las matemáticas. B) Como motivación, para ganar el interés de los estudiantes en el tema que se va a explicar. C) Como diversión, donde se busca tanto la motivación como la propia diversión del estudiante. D) Como vehículo, a través de los cuales los alumnos aprenden nuevos conceptos o desarrollan habilidades. E) Como práctica, para reforzar habilidades y conceptos aprendidos previamente.

4. Investigaciones que se están realizando Representaciones Problemas no rutinarios El papel del profesor Entornos informáticos

5. Problemas como Ángel está vendiendo gorras. La primera semana vendió ©©©©©©©©© La segunda ©©© La tercera ©©©©©© La cuarta ?? ¿Cuántas gorras vendió en la cuarta semana sabiendo que la media es 7?

6. Problemas como Fíjate en la siguiente figura: ¿Cuántos bloques son necesarios para construir un dibujo de 5 cuadrados de base? ¿y para uno de 20?

7. La resolución de problemas Un capitán sube a su barco 26 gallinas y 30 conejos. ¿Cuál es la edad del capitán? ****** Si un niño tiene 7 lápices y le quitan 7, ¿podrá escribir? ****** En un cesto hay 35.486 huevos ¿Cuántos pares de huevos hay?

8. CUBOS En esta fotografía puedes ver seis dados, etiquetados desde la (a) a la (f). Hay una regla que es válida para todos los dados: La suma de los puntos de dos caras opuestas de cada dado es siempre siete. Escribe en cada casilla de la tabla siguiente el número de puntos que tiene la cara inferior del dado correspondiente que aparece en la foto.

9. Dificultades en la resolución de problemas ¿Qué dificultades presentan los alumnos en la resolución de problemas de matemáticas? Resolución de problemas vs comprensión lectora

10. Dificultades en la resolución de problemas Falta de comprensión del enunciado del problema Por falta de comprensión lectora, porque no dominan el vocabulario empleado, porque no tienen interiorizadas las magnitudes, porque las situaciones planteadas no son familiares. Dificultad para reconocer la estrategia a seguir Dificultad para saber en qué orden hay que hacer las operaciones…

11. Dificultades en la resolución de problemas CONOCIMIENTOS DEL ESQUEMA (ESTRUCTURA) Hay dos tipos de esquemas básicos: a) PROBLEMAS TIPOS: Problemas de “sumar”, “restar, “multiplicar”, “dividir”, “mezclas”, “escalas”, “grifos”, “interés”, “máximos y mínimos”, “triángulos”, “movimientos”, “proporcionalidad”, etc. b) ESQUEMAS SEMÁNTICOS En los problemas aditivos (cambio, combinar, comparar e igualar) y en los multiplicativos (razón (reparto o agrupamiento), comparar y producto cartesiano). CONOCIMIENTOS OPERATIVOS Necesita saber hacer las operaciones matemáticas: sumar, restar, multiplicar, dividir, con decimales, con fracciones, con números enteros, resolver ecuaciones, etc.

12. ¿Qué estrategias usan los alumnos? Fijarse en palabras clave: quitar, total, cada uno, repartir…. Fijarse en los números, si se pueden sumar, si se pueden restar,… Fijarse en la página del libro de texto Recordar un problema similar ya resuelto

13. Algunas creencias acerca de la resolución de problemas A) Siempre hay una forma exacta de resolver cualquier problema. B) Las matemáticas (y la resolución de problemas) es una actividad solitaria. C) Todos los problemas deben resolverse en 5 minutos o menos, pasado este tiempo es que no lo sabes resolver. D) Las demostraciones formales no tienen nada que ver con procesos de descubrimiento o invención. E) Los problemas matemáticos escolares tienen muy poco o nada que ver con el mundo real.

14. Las matemáticas en la LOE g) Desarrollar las competencias matemáticas básicas e iniciarse en la resolución de problemas que requieran la realización de operaciones elementales de cálculo, conocimientos geométricos y estimaciones, así como ser capaces de aplicarlos a las situaciones de su vida cotidiana

15. Las matemáticas en la LOE Los contenidos asociados a la resolución de problemas constituyen la principal aportación que desde el área se puede hacer a la autonomía e iniciativa personal . La resolución de problemas tiene, al menos, tres vertientes complementarias asociadas al desarrollo de esta competencia: la planificación, la gestión de los recursos y la valoración de los resultados.

16. Las matemáticas en la LOE La planificación está asociada a la comprensión en detalle de la situación planteada para trazar un plan y buscar estrategias y, en definitiva, para tomar decisiones. La gestión de los recursos incluye la optimización de los procesos de resolución La evaluación periódica del proceso y la valoración de los resultados permite hacer frente a otros problemas o situaciones con mayores posibilidades de éxito.

17. Las matemáticas en la LOE En la medida en que la enseñanza de las matemáticas incida en estos procesos y se planteen situaciones abiertas, verdaderos problemas, se mejorará la contribución del área a esta competencia. Actitudes asociadas con la confianza en la propia capacidad para enfrentarse con éxito a situaciones inciertas están incorporadas a través de diferentes contenidos del currículo.

18. Las matemáticas en la LOE Resolver problemas (aritméticos, geométricos, de medida) explicando oralmente y por escrito el significado de los datos, de la situación planteada, el proceso seguido y las soluciones obtenidas

19. Los problemas matemáticos en la educación primaria Desarrollar una estrategia general de resolución de problemas Trabajar diferentes tipos de problemas

20. Estrategia de resolución de problemas - COMPRENDER EL PROBLEMA -DISEÑAR UN PLAN -EJECUTAR EL PLAN -REVISAR LA SOLUCIÓN

21. Tipos de problemas Problemas bien definidos Problemas mal definidos Invención de problemas Problemas de razonamiento lógico y uso de estrategias

22. Problemas bien definidos Acciones manipulativas y de forma oral A partir de imágenes (gráficos figurativos y no figurativos) A partir de enunciados escritos En contextos aritméticos, geométricos, de medida, de azar y estadística

23. Tipos de problemas Problemas mal definidos Problemas donde faltan datos Problemas donde sobran datos Problemas abiertos …

24. Invención de problemas Problemas donde faltan los datos, la pregunta,… - Luis compró un cuaderno de 1 euro y un lápiz de 0,25 euros - ¿Cuánto dinero le devuelven a Rosa? - Los refrescos costaron 4,75 euros. El bocadillo 2 euros . Se comieron 3 bocadillos. La guagua costó 1,13 euros por cada uno de los amigos

25. Invención de problemas Problemas donde nos dan El resultado: 103 Una operación 24+167 Una gráfica Un dibujo Un recorte de periódico

26. Tipos de problemas Problemas de razonamiento lógico y uso de estrategias Problemas de lógica Problemas que se resuelven mediante heurísticos Juegos de estrategias Problemas que se resuelven mediante el uso de materiales didácticos

27. L a resolución de problemas aritméticos En Educación Infantil hay que trabajar acciones que impliquen juntar, separar, reiterar, repartir y agrupar. En Educación Primaria hay que trabajar problemas que impliquen sumar, restar, multiplicar y dividir.

28. Problemas de dividir para Infantil Tenemos un ferry para trasladar los coches de una isla a otra. Si sólo puede llevar 3 en cada viaje, ¿cuántos viajes necesita hacer para transportar 15 coches? Tenemos 5 ferrys para trasladar de una vez 15 coches de una isla a otra. Todos los ferrys llevan el mismo número de coches. ¿Cuántos coches debe llevar cada ferry?

29. Resolución de problemas aritméticos Juan tiene en su colección 91 sellos y Ángel en la suya 27 sellos menos ¿Cuántos sellos tiene Ángel? 91 - 27 64 Ángel tiene 64 sellos

30. Problemas aritméticos RELACIÓN PARTES-TODO Constituye la base del razonamiento matemático, que tiene su equivalente en las acciones de agrupar y descomponer, base del sistema de numeración decimal y de las operaciones elementales. Esta estrategia permite determinar, a partir de la representación global y de las relaciones partes-todo, el tipo de algoritmo que se debe utilizar.

31. Problemas aditivos Son problemas que se resuelven con una suma o una resta. Juan tiene 5 lápices y le dan 2 lápices más. ¿Cuántos lápices tendrá Juan en total? 5 + 2 = ? María tiene 5 lápices. Juan tiene 2 más que María. ¿Cuántos lápices tiene Juan? 5 + 2 = ? Se dividen en cuatro categorías: Cambio, combinación, comparación e igualación.

32. Categorías semánticas El CAMBIO se origina cuando se da una cantidad inicial y un cambio o variación, debiéndose determinar la cantidad final. ci--------cambio--------cf Juan tiene 5 lápices y le dan 2 lápices más. ¿Cuántos lápices tendrá Juan en total?

33. Categorías semánticas La COMBINACIÓN se origina cuando se dan dos cantidades iniciales y le pedimos a los alumnos el resultado. C1 y C2 ---- cfinal En una mesa hay 3 niños y 2 niñas. ¿Cuántas personas hay en total?

34. Categorías semánticas COMPARAR: hay dos cantidades numéricas y se debe establecer qué cantidad es mayor o menor y cuál es la diferencia entre ambas. María tiene 5 lápices. Juan tiene 2 más que María. ¿Cuántos lápices tiene Juan?

35. Categorías semánticas Igualación: Es una mezcla entre un problema de comparación y un problema de cambio. Hay una acción que se ejecuta entre los dos conjuntos comparados con el fin de igualarlos. Juan tiene 5 lápices. Si coge 2 más tendrá igual número que María. ¿Cuántos lápices tiene María?

36. DIFERENTES REPRESENTACIONES Representaciones conjuntistas Máquina operadora de Dienes

37. DIFERENTES REPRESENTACIONES Más representaciones conjuntistas

38. DIFERENTES REPRESENTACIONES Recta real Otros diagramas cambio comparación combinación

39. DIFERENTES REPRESENTACIONES Regletas Cuisenaire cambio combinación comparación

40. Representación para los problemas de cambio y combinación

41. Representación para los problemas de comparación e igualación

42. Problemas multiplicativos Se resuelven mediante una multiplicación o una división. La multiplicación : Se conoce el valor de una parte y el número de partes y se busca el valor total. La división : Se conoce el total y el valor de una parte y se busca el número de ellas, o se conoce el total y el número de partes y se busca el valor de una parte. Se dividen en tres categorías: Razón, comparación y producto cartesiano

43. Problemas multiplicativos Razón - de multiplicar: hay una proporción simple directa entre las cantidades - de dividir: conocemos el valor total y el valor de una parte, y lo que tratamos de hallar es el número de partes (división-partición) o conocemos el valor total y el número de partes y queremos hallar cuánto vale una parte (división-reparto)

44. Problemas multiplicativos Razón Hay 5 estantes de libros en la habitación de María. María puso 8 libros en cada estante. ¿Cuántos libros puso María en su estantería? Hay 40 libros en la habitación de María. Hay 5 estantes. ¿Cuántos libros hay por estante? Hay 40 libros en la habitación de María. Hay 8 libros en cada estante ¿Cuántos estantes hay?

45. Problemas multiplicativos Comparación Se trabaja con dos colecciones, en las que la mayor contiene un número exacto de veces a la menor. Si nos dan la menor y el número de veces que está contenida: problema de multiplicar; Cuando conozcamos la colección mayor y la menor, o bien, aquella y el número de veces que contiene a ésta: problema de división.

46. Problemas multiplicativos Comparación 1. Luis tiene 6 caramelos. Marta tiene 5 veces tantos caramelos como tiene Luis ¿Cuántos caramelos tiene Marta? 2. Luis tiene 6 caramelos. Marta tiene 30 caramelos ¿Cuántas veces tiene Marta los caramelos que tiene Juan? 3. Marta tiene 30 caramelos. Marta tiene 5 veces tantos caramelos como tiene Luis. ¿Cuántos caramelos tiene Luis?

47. Problemas multiplicativos Producto cartesiano Hay una composición cartesiana de dos colecciones. -de multiplicación si conocemos las colecciones que vamos a emparejar, y -de división si se conoce una de estas colecciones y la colección final de parejas y se busca el valor de la otra colección. Se recomienda el uso del diagrama de ÁRBOL o diagramas de doble entrada.

48. Problemas multiplicativos Producto cartesiano Si tenemos 2 camisetas y 3 pantalones de fútbol, todos distintos entre sí ¿cuántos equipajes diferentes podemos formar cogiendo un pantalón y una camiseta? Un restaurante ofrece 20 menús diferentes combinando un primer plato y un postre. Si hay 4 postres diferentes ¿cuántos primeros platos hay?

49. Propuesta de organización por ciclos x x Prob. con dos o más operaciones X x x Prob. Multip. y div (razón y comparar) (producto cartesiano X X X X X X* Prob sumar y restar (combinar y cambio) Comparación e igualación Tercero (10-12) Segundo (8-10) Primer (6-8)

50. Problemas que aparecen en los libros de texto (Santillana) Problemas de sumar 0 - 0 0 0 Igualación 1 - 0 1 0 Comparación 54 - 18 12 24 Combinación 10 - 6 2 2 Cambio total 4ºy 5º 3º 2º 1º

51. Problemas que aparecen en los libros de texto (Santillana) Problemas de restar 3 - 1 0 2 Igualación 11 - 3 1 7 Comparación 8 - 4 1 3 Combinación 41 - 11 10 20 Cambio total 4ºy 5º 3º 2º 1º

52. Problemas que aparecen en los libros de texto (Santillana) Problemas de multiplicar 1 49 3º 2 55 2º Comparación Razón

53. Problemas que aparecen en los libros de texto (Santillana) Problemas de dividir 5 16 24 3º 2 18 11 2º Comparación Razón Reparto-Agrupam

54. PROPUESTA DE ORGANIZACIÓN POR CICLOS x x Prob. con dos o más operaciones X x x Prob. Multip. y div (razón y comparar) (producto cartesiano X X X X X X* Prob sumar y restar (combinar y cambio) Comparación e igualación Tercero (10-12) Segundo (8-10) Primer (6-8)

55. Una ficha de un alumno

56. Un modelo ENUNCIADO-HISTORIA El niño escribirá en este apartado el enunciado del problema, procediendo luego a su lectura, tratando de comprender todos y cada uno de sus términos (para lo cual es preciso utilizar un vocabulario y unas magnitudes adecuadas en problemas familiares). GRÁFICO-VIÑETA El niño ha de dibujar la situación planteada en el problema. ¿QUÉ DATOS TE DAN? ¿QUÉ DATOS TE PIDEN ? Estas dos preguntas le ayudan a reforzar la comprensión del problema. CALCULA LO QUE TE PIDEN SIN UTILIZAR FORMULAS En este apartado el alumno podrá resolver el problema manipulativamente, usando el modelo apropiado que represente la situación y usando cualquier heurístico específico. OPERACIONES ESCRIBE LA HISTORIA CON EL RESULTADO OBTENIDO

57. Un modelo A un congreso de médicos han asistido 320 especialistas del corazón y 137 especialistas en huesos. ¿Cuántos médicos han asistido al congreso? GRÁFICO (VIÑETA) ¿QUÉ DATOS TE DAN? ¿QUÉ DATO TE PIDEN? CALCULA LO QUE TE DAN SIN HACER OPERACIONES RESULTADO OPERACIONES RESULTADO ¿SON IGUALES LOS RESULTADOS ANTERIORES? ESCRIBE LA HISTORIA CON EL RESULTADO OBTENIDO

58. ESTRUCTURAS DE PENSAMIENTO Las operaciones elementales con números naturales deben estar contextualizadas en situaciones reales aplicadas a problemas cotidianos fomentar las estructuras de pensamiento típicas de estas edades que están coordinadas por los esquemas PARTES-TODO y por las categorías de CAMBIO, COMBINACIÓN, COMPARACIÓN e IGUALACIÓN.

59. Problemas mal definidos Acciones manipulativas y de forma oral A partir de imágenes (gráficos figurativos y no figurativos) A partir de enunciados escritos Donde falten datos o sobren datos

60. Problemas mal definidos Problemas abiertos Tengo monedas de 1 céntimo, 2 céntimos y 5 céntimos en el bolsillo. Si saco tres monedas ¿cuánto dinero puedo haber sacado?

61. Distintos problemas Problemas que requieran un análisis de la incógnita Luis tiene 8 euros y María 4. ¿Cuántos euros tienen entre los dos? Cambiar la pregunta : ¿tienen dinero suficiente para comprar un libro que cuesta 10 euros ?

62. Distintos problemas Problemas que se puedan resolver de más de una forma Luis tiene 2 euros. Quiere comprar un cuaderno que vale 1,10 euros y un bolígrafo que vale 0,80 euros. ¿Tendrá dinero para comprar las dos cosas?

63. Distintos problemas Problemas con demasiados datos, con datos escasos o con datos incorrectos Juan posee 30 gallinas y 8 ovejas. Luis solamente 25 gallinas. ¿Cuántas gallinas poseen entre los dos? En una comida se utilizaron 680 gramos de pescado para 4 personas ¿cuánto costó la comida? Se quiere construir un depósito de agua con una capacidad de 6000 litros ¿qué dimensiones debe tener? Luis tiene que recorrer 125 km en bicicleta para ir de Santa Cruz a Los Gigantes. El primer día recorre 30 km, el segundo día 80 km y el tercero 45 km ¿Cuántos km le quedan por recorrer?

64. Distintos problemas Problemas con más de una solución Luis va al estanco con 3 euros. Los chupa-chups cuestan 0,50 euros y los chicles 1 euro. ¿Qué puede comprar Luis? Problemas que no tienen solución Compré 80 objetos entre gomas y lápices por 3 euros, 50 lápices a 0,50 euros y las gomas a 0,30 euros. ¿Cuántas gomas compré?

65. Distintos problemas Problemas cuya solución está en el propio texto ¿Cuántos juguetes habría que fabricar si se necesitan 9184 y aún faltan 1314? Problemas que tengan el número cero como solución En un supermercado habían 108 docenas de huevos, de ellos se vendieron 1296 ¿cuántos huevos quedan por vender?

66. Distintos problemas Problemas sin datos numéricos Un automovilista viaja de Los Llanos de Aridane a Santa Cruz de la Palma, al mismo tiempo otro automovilista viaja de Santa Cruz de la Palma a Los Llanos de Aridane por la misma carretera ¿Cuál de los dos está más lejos de Santa Cruz de la Palma cuando se encuentran?

67. Distintos problemas Problemas donde faltan los datos, la pregunta,… - Luis compró un cuaderno de 1 euro y un lápiz de 0,25 euros - ¿Cuánto dinero le devuelven a Rosa? - Los refrescos costaron 4,75 euros. El bocadillo 2 euros . Se comieron 3 bocadillos. La guagua costó 1,13 euros por cada uno de los amigos

68. Distintos problemas Problemas con datos absurdos Luisa invitó a 6 amigas y a 3 amigos a su fiesta de cumpleaños. ¿Cuántos años cumplía? Problemas que plantean relaciones falsas Luis tarda en ir de su casa a la escuela 15 minutos, ¿cuántos minutos tardarán entre Luis, Juan y Pedro?

69. Problemas de razonamiento lógico y uso de estrategias - Uso de heurísticos específicos - Problemas de lógica - Juegos de estrategias

70. Proceso de resolución de problemas Una ESTRATEGIA es una técnica general de resolver problemas. Las estrategias no garantizan que se encuentre una respuesta, pero guiarán la solución del problema. Los HEURÍSTICOS ESPECÍFICOS son operaciones mentales, típicamente útiles en la resolución de problemas matemáticos. Son "reglas" o "modos de comportamiento que favorecen el éxito.

71. Heurísticos específicos Recordar un problema similar (analogía) Conjeturar y comprobar (ensayo y error) Simplificar Buscar regularidades Eliminar Construir modelos Empezar un problema desde atrás

72. El tablero del ajedrez Alguien me dijo una vez que hay 204 cuadrados en un tablero de ajedrez ¿Tenía razón? Usa algo que te ayude Anota lo que haces Trabaja sistemáticamente No te preocupes si te bloqueas

73. El tablero del ajedrez ¿Qué heurístico has usado? -recordar un problema similar -simplificar el problema -buscar una regularidad o patrón

74. Recordar un problema similar o analogía Recordar un problema similar resuelto con anterioridad. Resolver antes un problema similar sencillo: con números más pequeños transformándolo en una situación “familiar” conocida con menos variables con figuras de la misma índole pero más simple ...

75. Conjeturar y comprobar (ensayo y error) Ensayo y error fortuito Ensayo y error sistemático. Ensayo y error dirigido. Preparar al niño para hacer conjeturas. Aplicar la estrategia a la resolución de problemas.

76. Conjeturar y comprobar (ensayo y error) ¿Podrías asignar valores numéricos a cada letra de forma que: UNO S E ND +UNO +MORE DOS MONEY

77. Conjeturar y comprobar (ensayo y error) ¿Puedes colocar los números 1,2,3,4,5,6,7,8 y 9 dentro de un cuadrado dividido en 9 casillas, de forma que una vez colocados todos la suma de cada columna, de cada fila, de cada diagonal sea la misma? A eso se le llama cuadrado mágico. Si crees que el cuadrado 3x3 es muy fácil te proponemos que lo hagas con el cuadrado 4x4 y con los números 1 al 16.

78. Conjeturar y comprobar (ensayo y error) 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 4 9 2 3 5 7 8 1 6

79. Conjeturar y comprobar (ensayo y error)

80. Conjeturar y comprobar (ensayo y error) Este es el mapa de un barrio de una ciudad. Está compuesto por manzanas de edificios separadas por calles que se Entrecruzan. En algún lugar del barrio está escondido un ladrón. El inspector de policía tiene que colocar a sus hombres de manera que cubran todos los lados de cada manzana, pero tiene que utilizar el menor número de policías posibles. Por desgracia, cada uno de los policías ve sólo a una manzana de longitud en cada dirección.

81. Conjeturar y comprobar (ensayo y error) Estas son algunas de las formas en que cada policía puede vigilar

82. Simplificar Plantear una situación equivalente pero más simple. Cambiar la forma: más fácil de comprender método más fácil de descubrir más fácil de resolver Se usa con otras estrategias. Técnicas: - números más pequeños particularizar - orden más familiar - ejemplos sucesivos - subproblemas dividir un problema en partes - secuencias - casos

83. Simplificar ¿Cuántos palíndromos hay entre cero y mil? (Un palíndromo es un número como el 525 que se lee de la misma manera de adelante atrás que de atrás adelante) A. ¿Cuántos números desde el 1 al 9 son palíndromos? B. ¿Cuántos números desde el 10 al 99 son palíndromos? C. ¿Cuántos números desde el 100 al 999 son palíndromos? Hay 108 palíndromos entre 0 y 1000.

84. Buscar regularidades ¿Cuál será el siguiente elemento de la serie: 1 , 2 , 3 , 6 , 11 , 20 , 37 , 68 , ...?

85. Eliminar Introduce el uso de la lógica en el nivel de entendimiento de los alumnos. Eliminar soluciones de un conjunto dado hasta obtener la correcta Elaborar una lista de posibles soluciones: mediante lógica y eliminación obtener la respuesta. Técnica: Selección cuidadosa de la primera pista (la más fácil, la que más elimina). Uso de las tablas para organizar la información (posibles soluciones). Uso de métodos: directo o indirecto (reducción al absurdo).

86. Eliminar De los números: 871 745 3625 2860 2582 l780 1937 1485 1375 1671 1455 1075 1690 2635 2590 señalar el o los que cumplen simultáneamente las siguientes propiedades: a) La suma de los dígitos es 16 b) El número posee más de tres dígitos c) Es múltiplo de 5 d) No es un número par e) Es menor que 2572

87. Construir modelos UN MODELO ES UN OBJETO O DIBUJO QUE SIRVE COMO AYUDA O APOYO PARA COMPRENDER Y RESOLVER UN PROBLEMA MATEMÁTICO O ENTENDER UN SISTEMA MATEMÁTICO ABSTRACTO Y SUS PROPIEDADES. Buscar o construir el modelo apropiado. Usar el modelo para: - organizar la información - facilitar la comprensión - resolver el problema Hay que enseñar a ELABORAR y USAR modelos. Hay que proveer de experiencias a los estudiantes.

88. Construir modelos El problema de la rana que sale de un pozo: Una rana que intenta salir de un pozo avanza cada día 3 metros y retrocede uno. Si el pozo tiene nueve metros ¿cuántos días tarda en salir?

89. Empezar desde atrás Ordenar secuencias de acciones desde el objetivo hasta la información inicial El objetivo ya se conoce Determinar las operaciones que nos llevan al estado inicial del que se ha derivado el objetivo La solución vendrá dada por el estado inicial o por la secuencia de pasos al revés.

90. Empezar desde atrás El dueño de un establecimiento vende los 2/3 de una pieza de tela y uno de los dependientes 1/5 del resto quedando 4 m. sin vender. ¿Cuántos metros mide la pieza?

91. Empezar desde atrás Una noche, una bruja me ofreció lo que parecía un buen negocio: “ Humano, te ofrezco un trato ¿Ves ese puente? Cada vez que lo cruces doblaré el dinero que llevas en tus bolsillos. ¿Y qué te tengo que dar yo a cambio?, contesté Poca cosa. Me conformo con que me des 240 euros cada vez que cruces el puente. Sin fiarme mucho, atravesé el puente y conté mi dinero. ¡Era cierto! Ahora tenía el doble que antes. Pagué a la bruja los 240 euros acordados y crucé de nuevo el puente. Mi dinero se multiplicó por dos. Pagué a la bruja su parte y crucé el puente por tercera vez. Entonces me di cuenta que solo tenía 240 euros que tuve que pagar a la bruja. Riéndose de mí, desapareció. ¿Cuánto dinero tenía al principio?

92. Vamos a resolver problemas CHÓCALA Se han reunido 30 maestros y maestras para estudiar cómo celebrar el día escolar de las Matemáticas que es el 12 de mayo. Al encontrarse todos se saludan con un apretón de manos ¿ Cuántas apretones de mano se dieron?

93. LOS APRETONES DE MANO 435 30 … 21 7 15 6 10 5 6 4 3 3 1 2 Apretones Personas

94. LOS APRETONES DE MANO En geometría Apretones= lados + diagonales= 30 + (30x27):2 En aritmética: (30 x 29) : 2 De forma lógica: Sean 4: A, B, C, D AB, AC, AD; BC, BD; CD : 3 + 2+ 1= 6 Con 30: 29 + 28 + 27 +…1= 435

95. Juegos de estrategias Los juegos de estrategias presentan una gran similitud en el proceso que siguen con la resolución de un problema: Leer el problema o las reglas del juego Explorar Llevar a cabo la estrategia Comprobar los resultados

96. Juegos de estrategias Primero en llegar a 100 Es un juego para dos personas. Material: Lápiz y papel Finalidad del juego: Obtener mediante la operación suma y los números del 1 al 10, el número 100 Reglas: Los jugadores hacen turnos para elegir cualquier número entero del 1 al 10 Mantener una suma continua de todos los números elegidos El primer jugador que haga que esta suma, llegue exactamente a 100, gana la partida. ¿Existe una estrategia ganadora?

97. Juego del Hex Este juego fue ideado por el matemático danés, Piet Hein, hacia el año 1942. Consiste en un mosaico de hexágonos regulares. Los tableros pueden ser de distintos número de hexágonos, pero en Primaria podríamos empezar con uno de lado seis. Es un juego para dos jugadores. El juego consiste en ir por turnos depositando una ficha sobre el tablero en hexágonos que no estén ocupados hasta llegar a formar un camino continuo de un lado del tablero hasta el opuesto. Las cuatro celdillas que están en los vértices del tablero pueden ser utilizadas por ambos jugadores.

98. Juego del Hex

99. AZAR Y ESTADÍSTICA CARRERA DE CABALLOS Objetivo: Entender los conceptos básicos de probabilidad: suceso imposible, suceso probable, incluso calcular la probabilidad de cada suceso. Hacer gráficas estadísticas y ser críticos con el factor azar.

100. Azar y estadística CARRERA DE CABALLOS Reglas de juego: -Todos los caballos juegan -Cada jugador apuesta por un caballo -Se tiran dos dados y el caballo con el número resultante de la suma avanza una casilla. -Gana el que primero llegue a la meta

101. Azar y estadística CARRERA DE CABALLOS Se analiza lo que cada caballo avanzó y se hace una gráfica estadística.

102. Azar y estadística CARRERA DE CABALLOS Preguntas: ¿por qué no se ha movido el caballo 1? ¿cuáles son las mejores pistas? ¿por qué? ¿ha ganado algún caballo de esas pistas menos preferidas (azar)?

103. Problemas con materiales: el geoplano Es un tablero, generalmente cuadrado, con un sistema de pivotes o clavos situados en determinados puntos del mismo; entre tales pivotes se extienden elásticos de distintos colores que nos permiten crear gran diversidad de situaciones geométricas. Las acciones son rápidas y los errores se rectifican y anulan fácilmente

104. Actividades: Construcciones de elementos geométricos utilizando el geoplano ¿Cuántos cuadrados distintos se pueden hacer en tu geoplano? Construye todos los triángulos diferentes que puedas, cuadriláteros, pentágonos, etc. ¿Puedes construir un triángulo equilátero? ¿Y un hexágono regular?

105. Problema ¿Habrá alguna manera de calcular el área contando los clavos que bordean la figura y los que quedan dentro? Intenta dibujar distintas figuras, haz una tabla y busca alguna regularidad Clavos alrededor Número lados Área Clavos dentro

106. Resolución de problemas y las NTICS Usa el coco http://sauce.pntic.mec.es/jdiego/ El tinglado http://www.tinglado.net/?id=problemas-matematicas-primaria Jclic http://clic.xtec.cat/es/jclic/index.htm

107. Trabajar un concepto: La simetría Doblando papel Dibujando en el papel Geoplano Mira Espejos

108. Problemas de Lógica Había una vez una madre, un padre y dos hijos que querían cruzar un río y no había ningún puente. ¿Cómo podrían cruzar? Entonces vieron a un hombre con una barca de remos. - ¿Podría prestarnos su barca?- le preguntó mamá Sí, claro- contestó el barquero- pero es una barca muy pequeña. Sólo cabe en ella una persona mayor o dos niños. -¿Podrán manejar los niños los remos? -volvió a preguntar Mamá. ¡Oh, sí! - dijo el barquero-, y también pueden dejar la barca en la otra orilla, si quieren ¿Puedes enseñarnos cómo se las arreglarán la madre, el padre y los dos hijos para cruzar el río en esa barca tan pequeña?

109. Problemas de Lógica Otras variantes del mismo problema. Un barquero tiene que hacer cruzar el río a un lobo, una cabra y una col, y en la barca sólo puede llevar a uno cada vez. ¿Cómo puede cruzarlos sin que la cabra se coma la col, ni el lobo a la cabra?

110. Problemas de Lógica Conceptos que se trabajan: - Ver que las estrategias son necesarias para resolver problemas -Utilización de modelos si es necesario -Usar algún tipo de registro de lo que van haciendo - Razonamiento lógico

111. Problemas de Lógica El hombre de los helados vende unos supercucuruchos, y cada uno tiene tres bolas de helado. Se pueden elegir tres sabores: fresa, vainilla o chocolate. ¿Cuántos cucuruchos distintos puede hacer el hombre de los helados con sus tres sabores? Si la bola de vainilla cuesta 50 céntimos de euro, la de fresa 75 céntimos de euro y la de chocolate 90 céntimos de euros, ¿cuánto cuesta cada cucurucho?

112. Problemas de Lógica Variantes: Se tienen tres rotuladores: uno amarillo, uno rojo y otro verde. ¿De cuántas maneras se pueden ordenar en un estante? Un payaso tiene una chaqueta con tres botones. ¿De cuántas maneras podemos ponerle uno rojo, otro amarillo y otro azul? Con tres colores ¿cuántas banderas distintas se pueden hacer? Concepto a trabajar : Combinación de elementos

113. Códigos de barras Los códigos de barras traducen una secuencia de números a una distribución de barras blancas y negras legibles por un lápiz óptico que permite actuar al ordenador asignando precios al producto (cajeros), listando pedidos (distribuidores, almacenes), etc. European Article Number es un sistema de Códigos de Barras adoptado por más de 100 países y cerca de un millón de empresas (2.003). En el año 2005 la asociación EAN se ha fusionado con la UCC para formar una nueva y única organización mundial identificada como GS1, con sede en Bélgica.

114. Código de barras El código EAN más usual es EAN13, constituido por 13 dígitos y con una estructura dividida en 4 partes:

115. Código de barras Los primeros dígitos del Código de Barras EAN no identifican el país de origen del producto, sino, únicamente a través de qué Organización Nacional se ha adscrito una empresa al Sistema EAN. Por ejemplo, en España se encarga de ello Aecoc y su código es el '84'. Referencia del ítem, compuesto de: Código de empresa. Es un número compuesto por entre 5 y 8 dígitos, que identifica al propietario de la marca. Código de producto. Completa los 12 primeros dígitos.

116. Códigos de barras ¿Cómo calcular el número de seguridad, el decimotercero? El proceso es: poner las cifras del código y debajo la secuencia 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3 y hacer las suma de los productos de las dos sucesiones. 8 4 1 4 2 3 7 0 0 0 1 5 1 3 1 3 1 3 1 3 1 3 1 3 8 x 1+4 x 3 +1 x 1 + 4 x 3 + 2 x 1 + 3 x 3 + 7 x 1 + 0 x 3 + 0 x 1 + 0 x 3 + 1 x1 + 5 x 3= 67 Si la suma hubiera acabado en cero, sería el cero, En caso contrario se asigna la diferencia que va desde la suma hecha a la decena siguiente. En este caso sería 70 – 67 = 3

117. Braille y su alfabeto ** El problema matemático: Averiguar de cuántas maneras distintas podía colocar un punto en la figura. ¿Puedes hacerlo tú? Y ¿de cuántas maneras podía colocar dos puntos? ¿y tres? ¿y cuatro? ?y cinco? ¿y seis? ** Elegir cuáles eran las configuraciones más adecuadas

118. Braille y su alfabeto Este problema permite: Trabajo metódico, reconocimiento de una secuencia, secuencias numéricas Solución: 0 puntos 1 colocación posible 1 6 2 15 3 20 4 15 5 6 6 1

119. Braille y su alfabeto Alfabeto Braille

120. Braille y su alfabeto

121. PLANIFICACIÓN DE SESIONES 1ª) Trabajar la estrategia general 2ª) Problemas mal definidos 3ª) Invención de problemas 4ª) Problemas de lógica 5ª) Problemas bien definidos 6ª) Problemas resueltos con materiales didácticos 7ª) Problemas resueltos en el ordenador

122. Pautas de trabajo Presentar los contenidos que queremos trabajar en forma de PROBLEMAS (no ejercicios) del entorno directo, que resulten motivadores y aprovechando todas las situaciones de aula de interés matemático.

123. Pautas de trabajo Para resolverlos: Manipular (Materiales y Recursos: regletas de Cuisenaire, bloques multibase, calculadora, tangram, geoplano, la venta, ordenadores, retroproyector, juegos de mesa, de pesos y medidas, de geometría, material doméstico y de desecho, espacios del colegio, etc.) Verbalizar Poner en papel lo observado: dibujos (gráfico), lenguaje escrito, simbólico matemático.

124. Pautas de trabajo CONTENIDO RECURSOS PARA LLEGAR A ÉL Nos podemos guiar por el orden de los temas del libro de texto. Vamos abordando los contenidos según la secuencia que tengamos, pero partiendo de problemas significativos del entorno Siempre los/las alumnos/as manipulan materiales antes de introducir el lenguaje gráfico y/o simbólico matemático para la comprobación y resolución de los problemas

125. Pautas de trabajo Seguir con la práctica habitual e introducir un día a la semana fijo para las nuevas actividades Para llevarla a cabo se debe integrar en la programación, eligiendo las actividades de cada semana en función de la programación de contenidos y enlazándolas con estos .

126. GUIÓN DE OBSERVACIÓN DE ACCIONES REALIZADAS En cuanto a presentar PROBLEMAS SIGNIFICATIVOS y del entorno directo: ¿Lo estoy haciendo? ¿Con qué frecuencia? ¿En qué mejora? Dificultades Cuando lo haga otra vez que debo tener en cuenta o cambiar...

127. GUIÓN DE OBSERVACIÓN DE ACCIONES REALIZADAS En cuanto a aprovechar las SITUACIONES DE APRENDIZAJE MATEMÁTICO que surgen en el día a día. ¿Cuáles? ¿Cuándo? ¿En qué mejora? Dificultades Que debo tener en cuenta para las próximas veces...

128. GUIÓN DE OBSERVACIÓN DE ACCIONES REALIZADAS En cuanto a la REPRESENTACIÓN DE LO MANIPULADO Y VERBALIZADO Gráfica Lingüística Matemática En cuanto a la GENERALIZACIÓN DE LOS APRENDIZAJES ¿Lo trabajado sirve para resolver problemas en otros contextos? ¿Los alumnos/as usan con confianza el lenguaje matemático para explicar el entorno?

129. FORO http://boards4.melodysoft.com/app?ID=proyecto_matematicas http://boards4.melodysoft.com/app?ID=proyecto_matematicas Melodysoft Foromanía Educación Enseñanza activa de la matemáticas

130. http://www.mathnasium.com.es MATHNASIUM es un centro de aprendizaje de las Matemáticas dónde los estudiantes de Educación Primaria y ESO tienen la oportunidad de practicar, con nuestros miles de ejercicios, su capacidad de raciocinio y de desarrollar su “Sentido del Número”. Los miembros de MATHNASIUM pagan una mensualidad que les permite frecuentar el Centro siempre que quieran, y por tanto tiempo como deseen.

131. http://www.mathnasium.com.es Tal como en un gimnasio se desarrolla el cuerpo, en MATHNASIUM se desarrolla el raciocinio. Con un programa de entrenamiento personalizado, cada estudiante tiene la oportunidad de reforzar sus conocimientos de Matemáticas, así como su confianza y auto-estima, haciendo que sea más fácil obtener resultados positivos. Y los resultados ya han sido probados por una entidad independiente. Por eso, esta es...