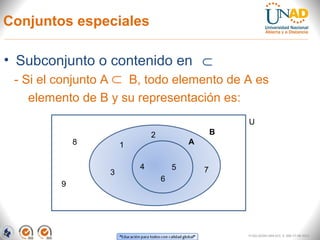
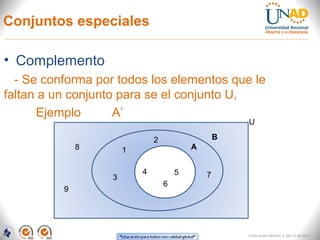
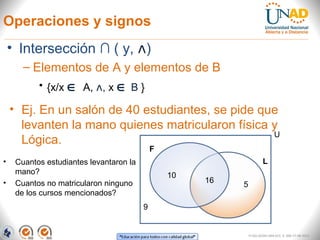
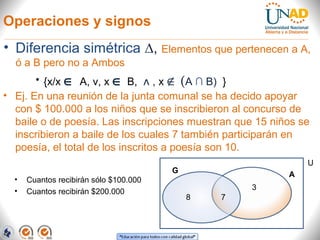
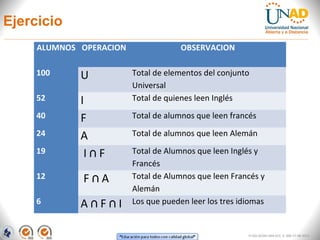
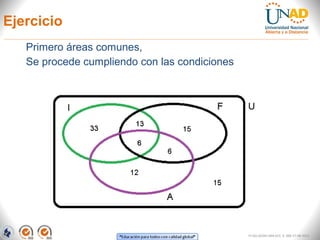
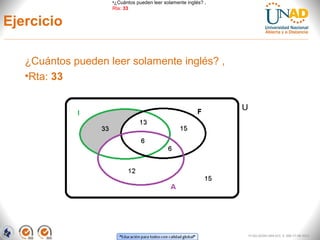
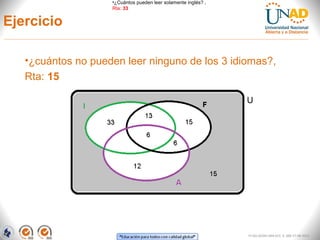
El documento aborda la teoría de conjuntos, presentando definiciones, tipos de conjuntos y sus representaciones gráficas mediante diagramas de Euler y Venn. Describe operaciones básicas como intersección, unión, diferencia y diferencia simétrica, proporcionando ejemplos aplicados a situaciones académicas y laborales. Finalmente, se incluye un ejercicio práctico sobre la lectura de idiomas entre alumnos, que ilustra el uso de estos conceptos.

1. Zona Centro/CEAD Sogamoso
Conjuntos
Sogamoso
11 de Septiembre de 2013
Ana Milena Corregidor Castro
Tutor ECBTI
FI-GQ-GCMU-004-015 V. 000-27-08-2011

2. Conjuntos
FI-GQ-GCMU-004-015 V. 000-27-08-2011
– Un conjunto es una colección de
objetos bien definidos.
– Se identifican mediante letras
Mayúsculas del Alfabeto
• Círculos de Euler o diagramas de
Venn.
• Son los diagramas que permiten la
representación de los conjuntos y sus
relaciones

3. Formas de Determinar un
conjunto
FI-GQ-GCMU-004-015 V. 000-27-08-2011
• Por extensión
– Describe nombrando cada uno de sus
elementos
• A {1,3,5,7,9}
• B {Amarillo, azul, rojo}
• Por comprensión
– Propiedad, regla o característica común
• A {Números impares menores que 10 }
• B {Los colores de la bandera de Colombia}

4. Conjuntos especiales
• Universal U
– Todos los elementos que hacen parte de un
estudio determinado.
• Vacío ⱷ
- No tiene elementos
• Unitario
- Un solo elemento
• Disyuntos
- No tienen elementos en común
FI-GQ-GCMU-004-015 V. 000-27-08-2011

5. Conjuntos especiales
• Subconjunto o contenido en
- Si el conjunto A B, todo elemento de A es
elemento de B y su representación es:
FI-GQ-GCMU-004-015 V. 000-27-08-2011
∩∩
∩ U
B
1 A
3
2
4 5
8
9
6
7

6. Conjuntos especiales
• Complemento
- Se conforma por todos los elementos que le
faltan a un conjunto para se el conjunto U,
Ejemplo A’
FI-GQ-GCMU-004-015 V. 000-27-08-2011
U
B
1 A
3
2
4 5
8
9
6
7

7. Operaciones y signos
• Intersección ∩ ( y, ᴧ)
– Elementos de A y elementos de B
• {x/x ∈ A, ,ᴧ x ∈ B }
• Ej. En un salón de 40 estudiantes, se pide que
levanten la mano quienes matricularon física y
Lógica.
FI-GQ-GCMU-004-015 V. 000-27-08-2011
U
L
10
F
5
9
16
• Cuantos estudiantes levantaron la
mano?
• Cuantos no matricularon ninguno
de los cursos mencionados?

8. Operaciones y signos
• Unión ( ó , v)
– Elementos de A ó elementos de B
• {x/x ∈ A, v, x ∈ B }
FI-GQ-GCMU-004-015 V. 000-27-08-2011
• Ej. Se ha solicitado a los empleados de una empresa que se
inscriban los que les gusta el futbol o el baloncesto para
conocer el número de personas con las que pueden contar
para los encuentros deportivos.
U
B
15
F
30
17
23
• Cuantos se inscribieron?
• Cuantos Juegan sólo Baloncesto?
• Cuantos juegan los dos deportes?
• Cuantos empleados tiene la empresa?

9. Operaciones y signos
• Diferencia - Elementos que pertenecen a A pero
no a B A – B
• {x/x ∈ A, ,ᴧ x ∉ B }
FI-GQ-GCMU-004-015 V. 000-27-08-2011
• Para la representación se debe tener en
cuenta no exceder el 100%
• Ej. En una población el 60% es ganadero, el 50% es agricultor;
se sabe que 30% es exclusivamente (Sólo) ganaderos y 20%
no pertenecen a ninguno de los grupos.
FI-GQ-GCMU-004-015 V. 000-27-08-2011
U
A
30%
G
20%
30%
20%

10. Operaciones y signos
• Diferencia simétrica ∆, Elementos que pertenecen a A,
ó a B pero no a Ambos
• {x/x ∈ A, v, x ∈ B, ,ᴧ x ∉ (A ∩ B) }
• Cuantos recibirán sólo $100.000
• Cuantos recibirán $200.000
• Ej. En una reunión de la junta comunal se ha decido apoyar
con $ 100.000 a los niños que se inscribieron al concurso de
baile o de poesía. Las inscripciones muestran que 15 niños se
inscribieron a baile de los cuales 7 también participarán en
poesía, el total de los inscritos a poesía son 10.
U
A
8
G
7
3

11. Ejercicio
FI-GQ-GCMU-004-015 V. 000-27-08-2
Una encuesta de 100 alumnos sobre idiomas
extranjeros, arrojó el siguiente resultado:
•52 pueden leer Inglés,
•40 pueden leer Francés,
•24 pueden leer Alemán,
•19 pueden leer Inglés y Francés,
•12 pueden leer Francés y Alemán
•y 6 pueden leer los 3 idiomas.
Responder los interrogantes
a- ¿Cuántos pueden leer solamente inglés?
b- ¿cuántos no pueden leer ninguno de los 3 idiomas?
c- ¿cuántos pueden leer sólo un idioma?.

12. Ejercicio
FI-GQ-GCMU-004-015 V. 000-27-08-2011
ALUMNOS OPERACION OBSERVACION
100 U Total de elementos del conjunto
Universal
52 I Total de quienes leen Inglés
40 F Total de alumnos que leen francés
24 A Total de alumnos que leen Alemán
19 I F∩ Total de Alumnos que leen Inglés y
Francés
12 F A∩ Total de Alumnos que leen Francés y
Alemán
6 A F I∩ ∩ Los que pueden leer los tres idiomas

13. Ejercicio
FI-GQ-GCMU-004-015 V. 000-27-08-2011
Primero áreas comunes,
Se procede cumpliendo con las condiciones

14. Ejercicio
FI-GQ-GCMU-004-015 V. 000-27-08-2011
¿Cuántos pueden leer solamente inglés? ,
•Rta: 33
•¿Cuántos pueden leer solamente inglés? ,
Rta: 33

15. Ejercicio
FI-GQ-GCMU-004-015 V. 000-27-08-2011
•¿cuántos no pueden leer ninguno de los 3 idiomas?,
Rta: 15
•¿Cuántos pueden leer solamente inglés? ,
Rta: 33

16. Ejercicio
FI-GQ-GCMU-004-015 V. 000-27-08-2011
•¿cuántos pueden leer sólo un idioma?.
•Rta: 33 + 12 +15 = 60
•¿Cuántos pueden leer solamente inglés? ,
Rta: 33

17. Unidad/Zona/grupo o equipo
funcional
FI-GQ-GCMU-004-015 V. 000-27-08-2011