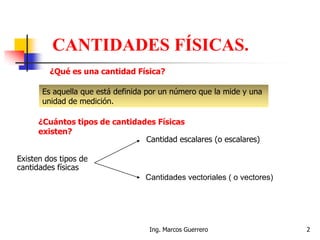
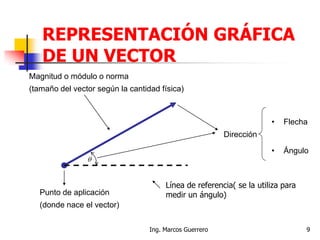
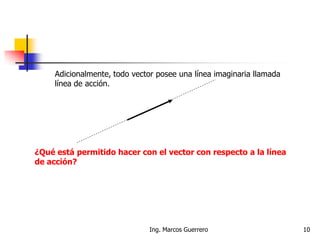
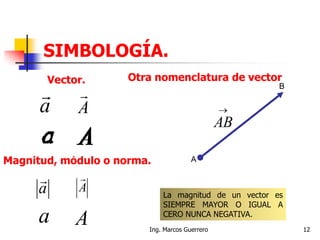
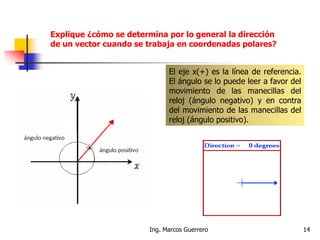
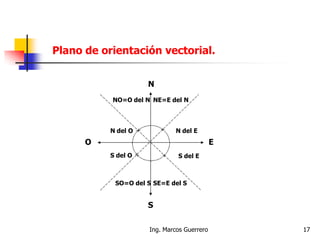
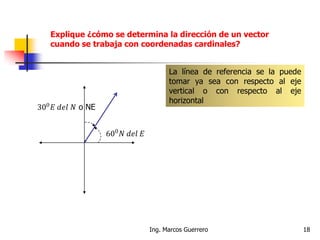
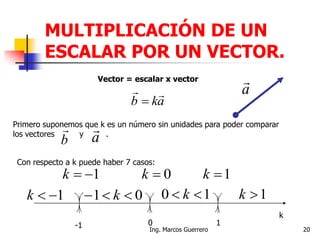
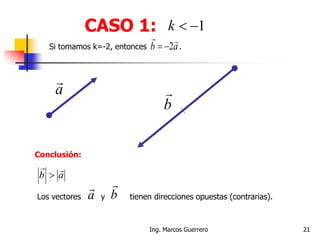
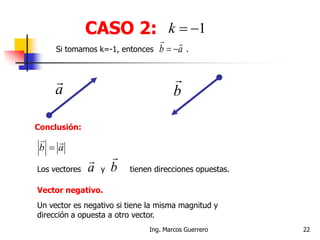
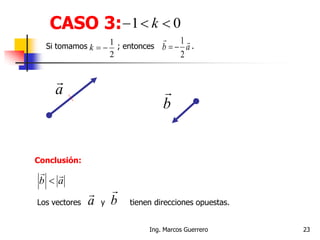
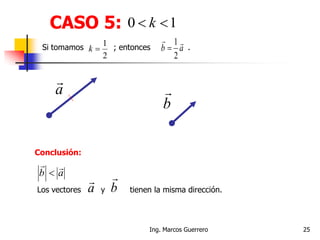
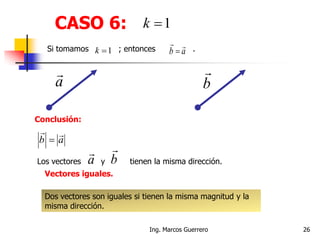
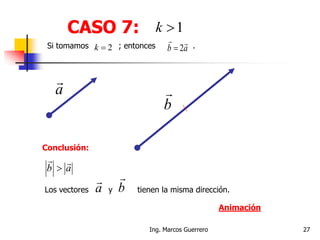
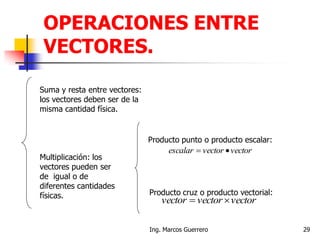
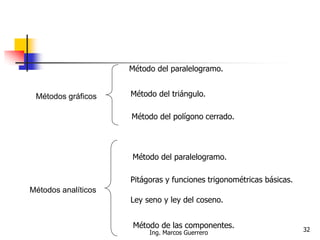
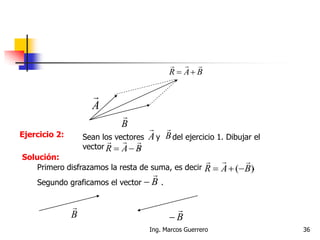
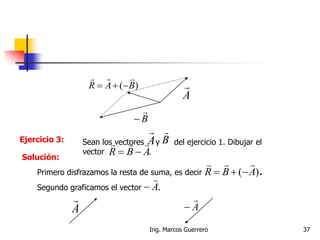
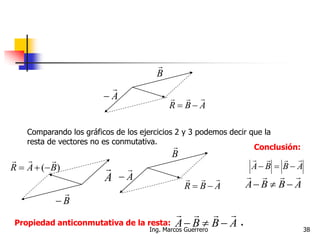
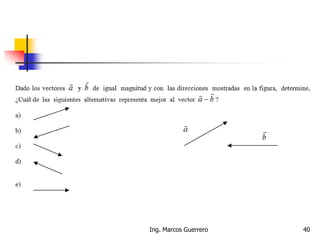
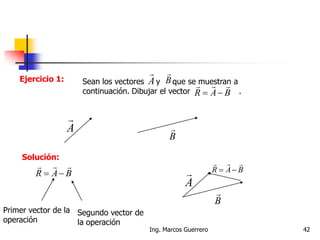
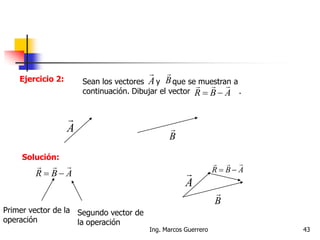
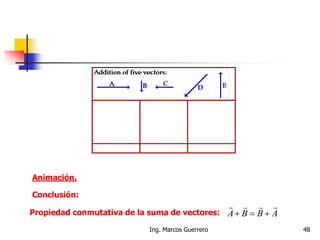
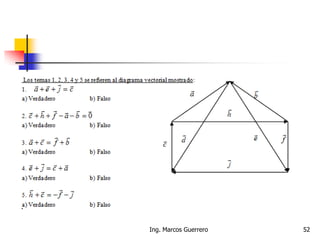
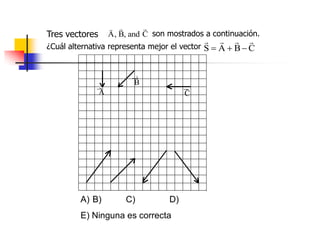
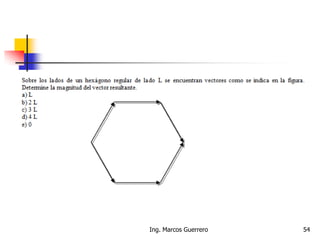
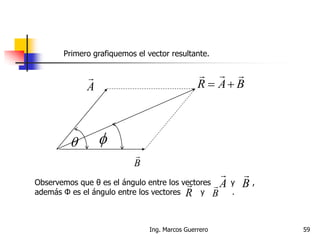
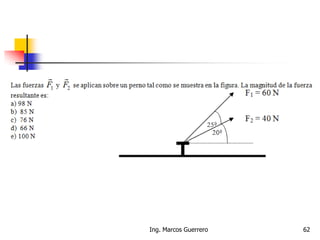
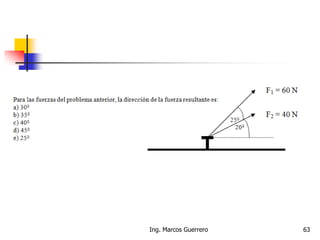
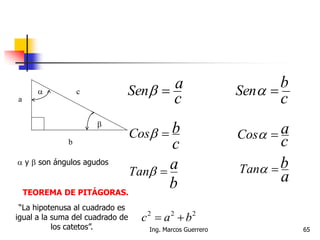
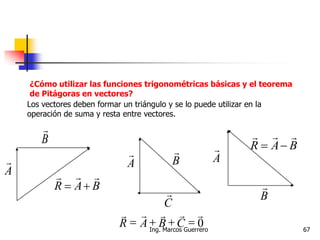
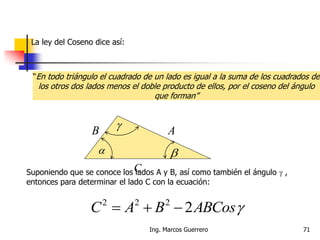
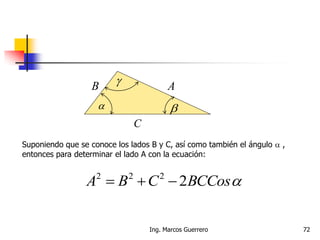
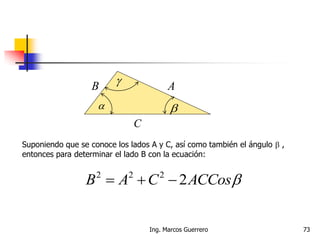
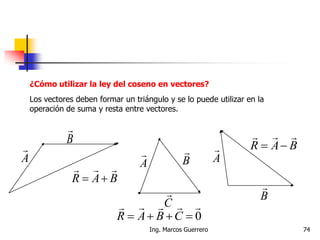
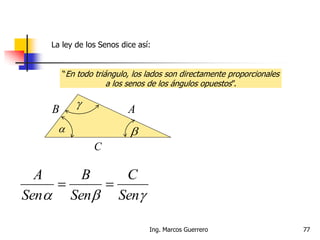
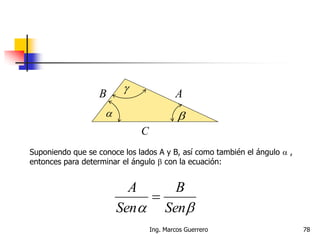
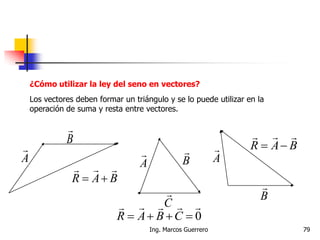
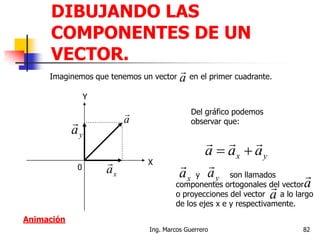
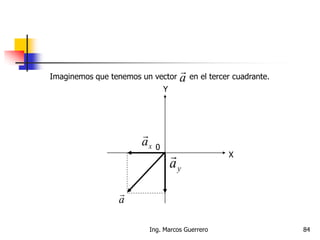
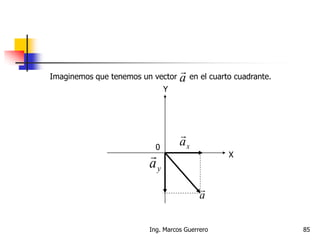
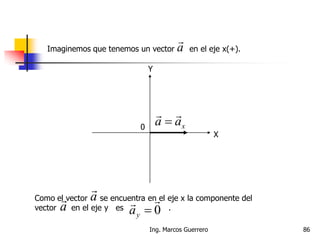
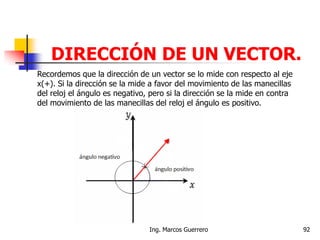
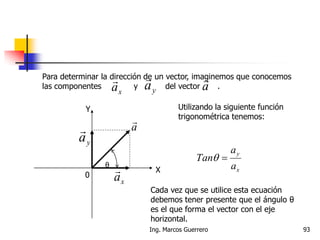
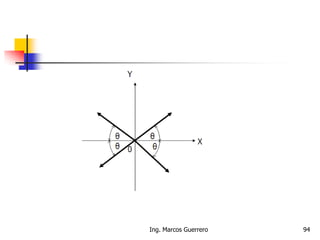
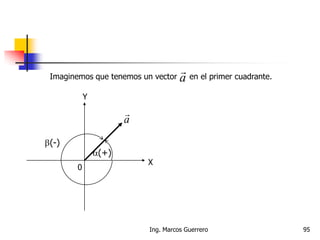
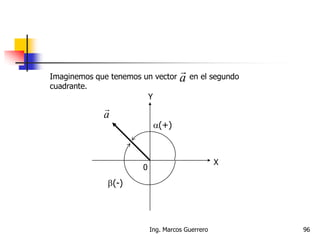
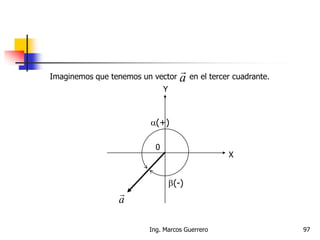
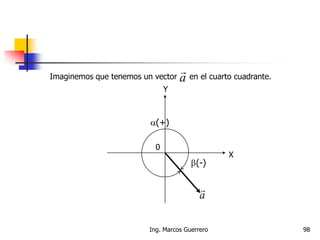
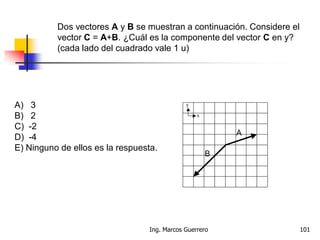
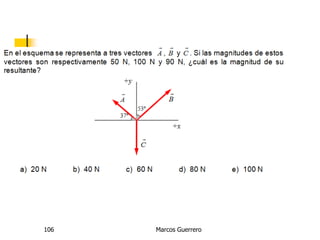
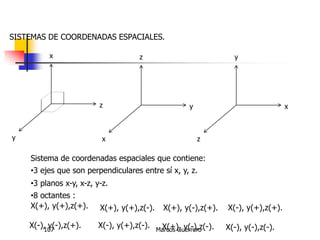
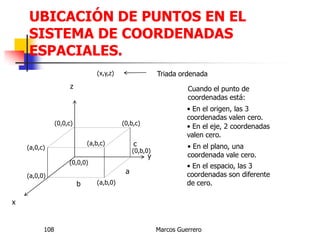
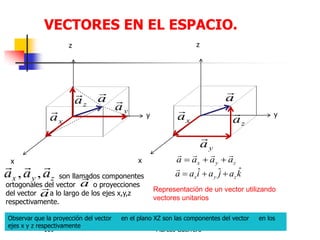
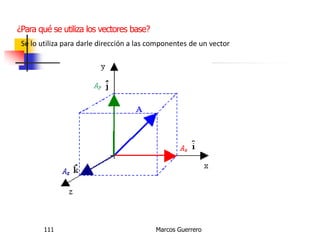
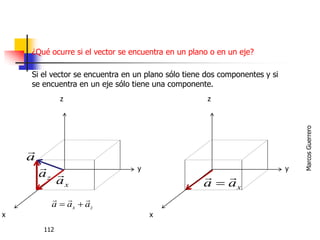
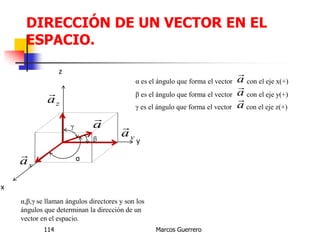
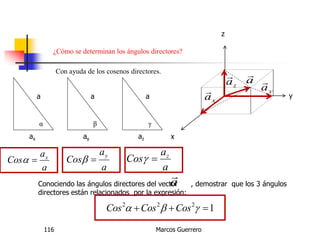
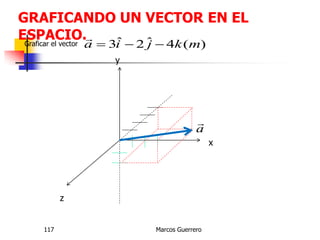
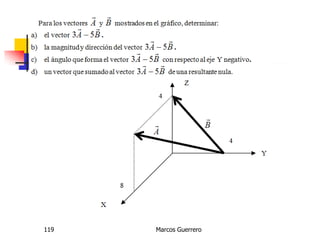
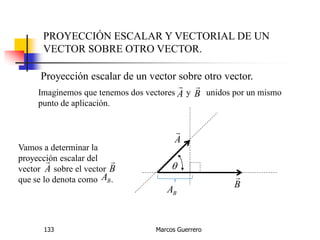
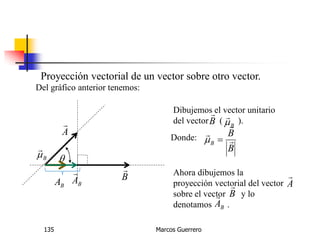
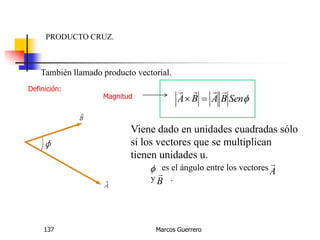
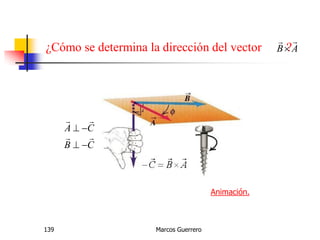
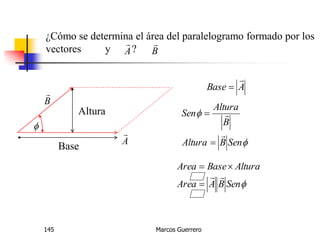
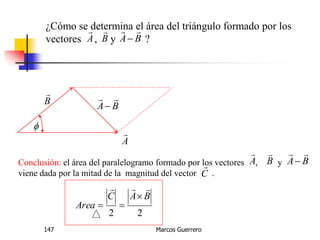
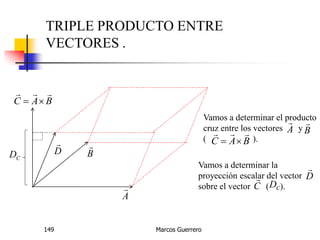
El documento describe los conceptos de cantidades escalares y vectoriales. Existen dos tipos de cantidades físicas: cantidades escalares, que tienen magnitud y unidad de medida, y cantidades vectoriales, que además de magnitud y unidad tienen dirección. Las cantidades vectoriales se representan gráficamente mediante flechas que indican su magnitud y dirección.