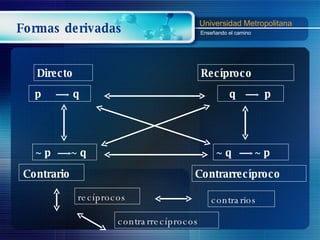
(1) El documento presenta los conceptos básicos de la lógica proposicional, incluyendo proposiciones simples, conectivos lógicos, tablas de verdad y diferentes formas del condicional. (2) Explica cómo construir tablas de verdad para proposiciones compuestas con diferentes números de proposiciones simples. (3) Discute las formas derivadas del condicional, incluyendo el recíproco, el contrario y el contrarrecíproco.

1. Lógica FBMM02 Semestre 0708A Profesor: Ricardo Escalante

2. Agenda Proposiciones Simples Conectivos y proposiciones compuestas. Tablas de verdad Construcción de tablas de verdad para proposiciones compuestas Formas derivadas del condicional Simbolización

3. Proposición Es un enunciado al cual se le puede asociar el concepto de verdadero o falso , pero no ambos . Ejemplos: La luna es cuadrada 7 es un número primo Las arañas son mamíferos ¿Son proposiciones? ¿Qué hora es? Por favor, cierre la puerta El 6 de abril de 1876 fue sábado D ice el Presidente : “ Todos en este país son unos mentirosos y esto es verdad”

4. Proposiciones compuestas Conectivos Conocido el valor de verdad de ciertas proposiciones, la lógica establece el valor de verdad de otras relacionadas con éstas. A éstas últimas se les conoce como proposiciones compuestas

5. Negación Si p es una proposición, entonces “no p” es la negación de p y se denota por: ~ p Ejemplo: p: Hoy es martes ~ p: Hoy no es martes ¿Qué sucede con la negación de p, siendo p verdadero? ¿Qué sucede con la negación de p, siendo p falso?

6. Negación Esto lo podemos escribir de una manera “compacta”, utilizando una tabla A esta tabla se le llama “tabla de certeza de la negación” p ~ p V F F V Posibilidades para la proposición p

7. Conjunción Si p y q son proposiciones, se llama conjunción de p y q a la proposición compuesta “p y q “ y se denota por: p  q Ejemplos: p: Hoy es martes q: La luna es cuadrada r: mañana es miércoles p  q :Hoy es martes y la luna es cuadrada p  r :Hoy es martes y mañana es miércoles

8. Conjunción Para construir la tabla de p  q, debemos considerar las diferentes alternativas de valores de verdad para p y para q: ¿Cuáles son ? Ambas verdaderas una V y la otra F ambas falsas p q p  q V V V V F F F V F F F F

9. Disyunción Si p y q son proposiciones, se llama disyunción de p y q a la proposición compuesta “p o q” y se denota por: p  q p q p  q V V V V F V F V V F F F

10. Disyunción Ser é cantante o futbolista p: Ser é cantante q: Ser é futbolista Simbolización: p  q p q p  q V V V V F V F V V F F F

11. Condicional Si p y q son proposiciones, se llama condicional de p y q a la proposición compuesta “si p, entonces q” y se denota por: p  q Ejemplos: Si no llueve (entonces) iremos a la playa Si me gano la lotería (entonces) me voy de viaje Si no estudio (entonces) no aprobaré Lógica

12. Condicional Veamos la tabla del condicional: p  q Conviene pensar en una “promesa” ..... Si no llueve (entonces) iremos a la playa p q p  q V V V V F F F V V F F V

13. Condicional El condicional es falso, sólo cuando el antecedente es verdadero y el consecuente es falso; es decir, cuando la “promesa” no se cumple. p q p  q V V V V F F F V V F F V

14. Condicional El condicional es muy importante en matemáticas, porque los Teoremas se expresan en forma condicional. Un Teorema será un condicional verdadero con hipótesis verdadera p q p  q V V V

15. Condicional y Teoremas En los Teoremas, al antecedente del condicional (p) se le llama Hipótesis y al consecuente (q) se le llama Tesis o Conclusión Los Teoremas requieren de una demostración; es decir, partiendo de una hipótesis verdadera, hay que demostrar que la Conclusión es verdadera.

16. Tablas de verdad Recordemos que el valor de certeza de una proposición compuesta depende de los valores de certeza de las proposiciones simples que la componen Para analizar los valores de certeza de una proposición compuesta, representamos todas las posibilidades de valores de verdad de las proposiciones simples, en un arreglo de tabla

17. Ejemplo con 2 proposiciones simples Construyamos la tabla de verdad para la siguiente proposición : (p  q)  (p  ~q) 4 filas de posibilidades p q V V V F F V F F p  q p  ~q V F F V F V F V ~q F V F V (p  q)  (p  ~q) F F F F

18. Ejemplo con 3 proposiciones simples ¿Cuántas posibilidades tendremos? 8 p q r V V V V V F V F V V F F F V V F V F F F V F F F

19. Ejemplo con 3 proposiciones simples Hacer la tabla de certeza para: (r  p)  ~(q  p) p q r V V V V V F V F V V F F F V V F V F F F V F F F r  p q  p ~(q  p) V V F V V F V V F V V F V V F F V F V F V F F V (r  p)  ~(q  p) F F F F F F V F

20. En resumen Una tabla de verdad para proposiciones compuestas que contienen: 1 proposición simple… tendrá 2 filas 2 proposiciones simples 3 proposiciones simples 4 proposiciones simples …… razonando inductivamente…….. n proposiciones simples 4 = 2 2 filas 8 = 2 3 filas 16= 2 4 filas 2 n filas

21. Formas de expresar un condicional……. Si es caraqueño , es venezolano ( p  q ) Es venezolano , siempre que sea caraqueño Es venezolano si es caraqueño Es suficiente que sea caraqueño para que sea venezolano Siempre y cuando sea caraqueño, será venezolano . Es necesario que sea venezolano para ser caraqueño TODAS ESTAS EXPRESIONES SE SIMBOLIZAN COMO: p  q

22. Partes de un condicional p  q antecedente Condición suficiente consecuente Condición necesaria

23. Formas derivadas del condicional Dado el condicional directo: p  q, el condicional ~ p  ~q se llama contrario y lo expresaríamos: “ si no p, entonces no q” Directo: p  q Si repruebo el examen, entonces me enojaré bastante Contrario: ~ p  ~q Si no repruebo el examen, entonces no me enojaré bastante

24. Formas derivadas del condicional Dado el condicional directo: p  q, el condicional q  p se llama recíproco y lo expresaríamos: “ si q, entonces p” Directo: p  q Si repruebo el examen, entonces me enojaré bastante Recíproco: q  p Si me enojo bastante , entonces reprobaré el examen

25. Formas derivadas del condicional Dado el condicional directo: p  q, el condicional ~ q  ~p se llama contrarrecíproco y lo expresaríamos: “ si no q, entonces no p” Directo: p  q Si repruebo el examen, entonces me enojaré bastante Contrarrecíproco: ~ q  ~p Si no me enojo bastante, entonces no repruebo el examen

26. Formas derivadas p q q p ~ p ~ q ~ q ~ p Directo Recíproco Contrario Contrarrecíproco recíprocos contrarios contrarrecíprocos

27. Ejemplo Hallar las formas derivadas del siguiente condicional: Si un número es par, entonces es múltiplo de 4. ……………………………………. ¿V o F? Falso (contraejemplo: 2) Recíproco : Si un número es múltiplo de 4 entonces es par. …………………………………..¿V o F? Verdadero!

28. Ejemplo Directo: p  q Si un número es par, entonces es múltiplo de 4. Contrario : ~ p  ~ q Si un número no es par, entonces no es múltiplo de 4 Verdadero!

29. Ejemplo Directo: p  q Si un número es par, entonces es múltiplo de 4. Contrarrecíproco : ~ q  ~ p Si un número no es múltiplo de 4, entonces no es par Falso….. 2 no es múltiplo de cuatro y es par ( antecedente verdadero, consecuente falso )

30. Ejercicios Escribir las formas derivadas para: a) ( r  ~ q )  p. b)Si yo digo sí, ella dice no. Construye una proposición verdadera que incluya un condicional, una conjunción, una disyunción y una negación (no necesariamente en ese orden), que conste de las componentes p, q y r con todas ellas falsas.

31. Ejercicios Escribe el recíproco, el inverso y el contrarrecíproco de cada una de las proposiciones siguientes: Si q, entonces r ~ p  (~ q ) ~p  ~ (r  q ) El sol brilla si estás feliz. Si tu automóvil no tiene aire acondicionado, no tendrás amigos.