Descargado 20 veces
Subido porjuliocesarfernades12
Julio saia
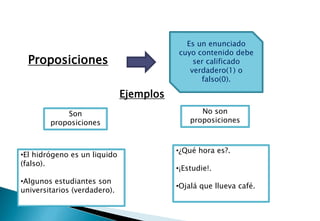
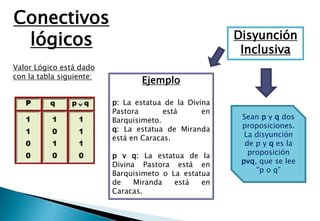
Este documento presenta una introducción a la lógica proposicional. Define conceptos clave como proposiciones atómicas y moleculares, conectivos lógicos como la negación, conjunción, disyunción, condicional y bicondicional, y tablas de verdad. También explica leyes como la de Morgan, tautologías, contradicciones, métodos de demostración como la demostración directa e indirecta, e inferencias como el modus ponens y modus tollens. Finalmente, establece la relación entre
Julio saia
- 1. REPUBLICA BOLIVARIANA DEVENEZUELA UNIVERSIDAD FERMIN TORO CABUDARE-ESTADO LARA Unidad1 Julio Cesar Fernandes López C.I.:20.473.791 Ingeniería en mantenimiento mecánico
- 2. Es un enunciado cuyo contenido debe Proposiciones ser calificado verdadero(1) o falso(0). Ejemplos Son No son proposiciones proposiciones •¿Qué hora es?. •El hidrógeno es un liquido (falso). •¡Estudie!. •Algunos estudiantes son •Ojalá que llueva café. universitarios (verdadero).
- 3. Proposiciones Operaciones atómicas o Veritativas simples Es cuando las proposiciones no contienen Los Conectivos u conectivos Operadores Lógicos lógicos. son símbolos o conectivos que nos permiten unir dos o más Proposiciones proposiciones, a molecular o partir de compuesta proposiciones dadas. Es cuando las proposiciones si contienen conectivos lógicos.
- 4. Conectivos lógicos Sea p una proposición, la negación de p es Negación otra proposición identificada por: ~ p, que se lee "no Tabla de verdad de los conectivos lógicos p", y cuyo valor lógico está dado por la negación de dicha proposición.
- 5. Conectivos lógicos Valor Lógico está dado con la tabla siguiente: Conjunción Ejemplo p: El Negro Primero peleó en Carabobo. Sean p y q dos q: Bolívar murió en proposiciones. Colombia. La conjunción r: Miranda nació en Coro. de p y q es la Entonces proposición p ^ q: El Negro Primero p^q, que se peleó en Carabobo y lee "p y q“. Bolívar murió en Colombia.
- 6. Conectivos lógicos Disyunción Inclusiva Valor Lógico está dado con la tabla siguiente: Ejemplo p: La estatua de la Divina Pastora está en Barquisimeto. Sean p y q dos q: La estatua de Miranda proposiciones. está en Caracas. La disyunción de p y q es la p v q: La estatua de la proposición Divina Pastora está en pvq, que se lee Barquisimeto o La estatua "p o q” de Miranda está en Caracas.
- 7. Conectivos lógicos Disyunción Valor Lógico está dado Exclusiva con la tabla siguiente: Ejemplo p: 17 es un número primo. q: 17 es un número par. Sean p y q dos p v q: ó 17 es un número proposiciones. La primo ó 17 es un número disyunción par. exclusiva de p y q es la proposición pvq, que se lee: “o p o q”.
- 8. Conectivos lógicos Ejemplo Valor Lógico está dado con la tabla siguiente: a: 2 + 1 = 3 si y sólo si 2< 3 b: 2 + 1 = 3 si y sólo si 2 > 3 c: 2 + 1 = 4 si y sólo si 2 > 3 d: 2 + 1 = 4 es condición necesaria y suficiente para que 2< 3. Sean p y q dos proposiciones. Se llama Bicondicional de pyq a la proposición p q, que se lee "p si sólo Bicondicional si q", o "p es condición necesaria y suficiente para q“.
- 9. Conectivos lógicos Ejemplo Valor Lógico está dado Así el condicional A C con la tabla siguiente: puede ser leído de las siguientes maneras: 1. Si A entonces C 2. C es condición necesaria para A Sean p y q dos proposiciones. El condicional con Condicional antecedente p y consecuente q es la proposición p q, que se lee “si p, entonces q”.
- 10. Tablas de Verdadde las formas proposicionales Ejemplo: Permiten determinar Dado el siguiente esquema molecular, construir su el valor de verdad tabla de valores de verdad: de una proposición Pasos para construir la tabla: compuesta y ( p q) (p r) depende de las 1. Determinamos sus valores de verdad 2 3 = 8 proposiciones combinaciones simples y de los 2. Determinamos las combinaciones: operadores que contengan.
- 11. Tablas de Verdadde las formas proposicionales 3. Adjuntamos a éste cuadro el esquema molecular y colocamos debajo de cada una de la variables sus valores de verdad :
- 12. Tautología y Contradicciones Proposición Tautológica o Contradicción Tautología Es aquella proposición Es aquella proposición molecular en la que los valores molecular en la que todos los de verdad que aparecen en su valores de verdad que aparecen tabla de verdad son todos 0 en su tabla de verdad son 1 independientemente de los independientemente de los valores de sus variables valores de sus variables. proposicionales que la forman. Ejemplo: Probar que pv~p es Ejemplo: Probar que p^~ p es una tautología. una contradicción. p v ~P p ^ ~P 1 1 0 1 0 0 0 1 1 0 0 1
- 13. Leyes del Algebrade Proposiciones 1.Leyes Idempotentes 5. Leyes de Identidad 1.1. p v p = p 1.2. p ^ p = p 5.1. p v f = p 5.2. p ^ f = f 2.Leyes Asociativas 5.3. p v v = v 5.4. p ^ v = p 2.1. (p v q) v r = p v (q v r) 2.2. (p ^ q) ^ r = p ^ (q ^ r) 6. Leyes de Complementación 3.Leyes Conmutativas 6.1. p v ~p = v (tercio excluido) 6.2. p ^ ~p = f (contradicción) 3.1. p v q = q v p 6.3. ~~p = p (doble negación) 3.2. p ^ q = q ^ p 6.4. ~v = f, ~ f = v 4.Leyes Distributivas 7. Leyes De Morgan 4.1. p v ( q v r ) = ( p v q ) ^ (p v r) 7.1. ~ ( p v q ) = ~ p ^ ~ q 4.2. p ^( q ^ r ) = ( p ^ q ) v (p ^ r) 7.2. ~ ( p ^ q ) = ~ p v ~ q
- 14. Leyes del Algebrade Proposiciones Otras Equivalencias Notables a. p->q = ~ p v q (Ley del condicional) b. p<-> q = (p->q) ^ (q->p) (Ley del bicondicional) c. p v q = ( p ^ ~q ) v ( q ^ ~p ) (Ley de disyunción exclusiva) d. p->q = ~q->~p (Ley del contrarrecíproco) e. p ^ q = ~(~p v ~q) f. ( (p v q ) -> r) = ( p -> r) ^ (q -> r) (Ley de demostración por casos) g. (p->q) = (p ^ ~ q-> f) (Ley de reducción al absurdo) Todas las equivalencias que aparecen en ambos cuadros pueden ser probadas. Para esto, sólo se tiene que verificar que el bicondicional correspondiente es una tautología.
- 15. Equivalencia e Implicación lógica Implicación lógica Proposiciones Equivalentes Sean A y B dos formas Sean A y B dos formas proposicionales. Se dice que A proposicionales. Diremos que A Implica Lógicamente a B, o es Lógicamente Equivalente a simplemente A implica a B, y se B, o simplemente que A es escribe: equivalente a B, y escribimos: A B ó AB, A B si el condicional A-> B es Si y sólo si la forma una tautología. bicondicional A B es una tautología.
- 16. Razonamiento Forma Proposicional de un Un razonamiento o Razonamiento una inferencia es la aseveración de que Un razonamiento con una premisas P1, P2, P3, P4, & proposición, llama .., Pn y conclusión C lo da conclusión es escribiremos en forma consecuencia de proposicional como: otras proposiciones dadas llamadas P1 premisas. P2 P3 P4 Diremos que un razonamiento es . válido o correcto si la conjunción de . premisas implica lógicamente la . conclusión, en otro caso se dice que Pn es no válido. ----- Un razonamiento que no es válido C es llamado “falacia”.
- 17. Métodos de Demostración Demostración Indirecta Demostración Directa Dentro de este método veremos En la demostración directa dos formas de demostración: debemos probar una implicación: p=>q. Método del Contrarrecíproco: Esto es, llegar a la conclusión q a Otra forma proposicional equivalente partir de la premisa p mediante a p->c nos proporciona la Ley del una secuencia de proposiciones en contrarrecíproco: las que se utilizan axiomas, definiciones, teoremas o p->c ~ c-> ~ P. propiedades demostradas previamente. Esta equivalencia nos proporciona otro método de demostración, llamado el método del contrarrecíproco, según el cual, para demostrar que p=>c, se prueba que ~ c=> ~p.
- 18. Métodos de Demostración Demostración Indirecta. Demostración por reducción al absurdo: Veamos que la proposición p => q es tautológicamente equivalente a la proposición (p ^ ~ q) => (r ^ ~ r) siendo r una proposición cualquiera, para esto usaremos el útil método de las tablas de verdad.
- 19. Inferencia 1.Modus Ponendo Ponens(MPP) (p-> q) ^ p => q p-> q p ---------- q 2. Modus Tollendo Tollens (MTT) (p->q) ^ ~ q=>~ p p->q ~q ----------- ~p 3. Silogismo Disyuntivo (S.D) (pv q) ^ ~ q=> p pvq ó pvq (pv q) ^ ~ p=> q ~q ~p --------- --------- p q
- 20. Inferencia 4. Silogismo Hipotético(S.H) (p q) (q r) (p r) p q q r ---------- p r 5. Ley de Simplificación pqp pq ó pq pqq ---------- ---------- p q 6. Ley de la Adición p p q p q ---------- ó --------- qpq pq pq 7. Ley de Conjunción ( p ) ( q) ( p q) p q --------- pq
- 21. Circuitos lógicos Ejemplo: Construir el circuito correspondiente a Los circuitos lógicos o redes de cada una de las conmutación siguientes expresiones: Los podemos identificar con una forma proposicional. Es decir, dada a) p ^ (q v r) una forma proposicional, podemos asociarle un circuito; o dado un circuito podemos asociarle la forma proposicional correspondiente.