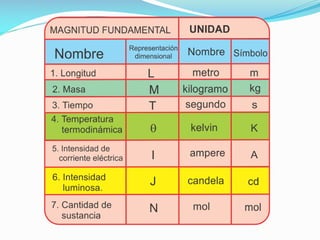
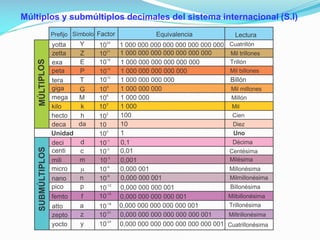
El documento aborda las magnitudes físicas y su clasificación en fundamentales, derivadas y auxiliares, además de su medición utilizando instrumentos específicos. Se establece el Sistema Internacional de Unidades (SI) y sus unidades de base y derivadas, junto con la notación científica para expresar números grandes y pequeños. También se explican las dimensiones físicas, su uso en ecuaciones y la importancia del principio de homogeneidad.

1. FÍSICA
Silvio Chávez Acevedo

2. Magnitudes

3. Estación total

4. Magnitudes
COLUMNA A: Magnitudes COLUMNA B:
Instrumentos de
medida
a) El ancho del salón. ( ) Termómetro
b) El tiempo que demora un atleta en
recorrer 400 metros planos.
( ) Tensiómetro
c) La temperatura del cuerpo humano. ( ) Barómetro
d) La intensidad de corriente eléctrica
que contiene una pila seca UM-1
(grande)
( ) Cronómetro
e) La presión arterial de una persona. ( ) Amperímetro
f) La presión atmosférica en la ciudad de
Huancayo.
( ) Metro patrón

5. MAGNITUDES
Magnitud física es todo aquello susceptible
a ser medido y ser expresado
cuantitativamente.
Toda magnitud física se puede medir,
utilizando instrumentos y unidades
apropiados.
Ejemplo: tiempo, masa, fuerza,
temperatura, velocidad, presión, etc.
Medir.- Es comparar una cantidad física
con otra de su misma naturaleza
considerada como unidad de medida.

6. Clases de magnitudes
a) Por su origen:
a1) Fundamentales o básicas
a2) Derivadas
a3) Auxiliares
b) Por su naturaleza:
b1) Escalares
b2) Vectoriales

7. Magnitudes fundamentales
Son aquellas elegidas como base, nombradas por el
Sistema Internacional de Unidades y en función a ellas
se expresan las demás magnitudes.
Las magnitudes fundamentales de acuerdo a la XI
Conferencia General de Pesas y Medidas de 1960, son 7:
Longitud, masa, tiempo, temperatura termodinámica,
intensidad de corriente eléctrica, intensidad luminosa y
cantidad de sustancia.

8. Magnitudes derivadas
Son aquellas magnitudes que están
expresadas en función de las magnitudes
fundamentales y suplementarias, entre
algunos de ellos tenemos:
El área, volumen, velocidad lineal,
velocidad angular, aceleración, densidad,
etc.

9. Magnitudes auxiliares o
suplementarias
Son aquellas que no han sido
consideradas ni como magnitudes
fundamentales ni derivadas; son 2:
Ángulo plano y ángulo sólido.

10. Magnitudes escalares
Son aquellas magnitudes que quedan bien
definidas al conocer su valor numérico y su
respectiva unidad física, no poseen dirección.
Ejemplo:

11. Magnitudes vectoriales
Son aquellas magnitudes físicas,
que además de tener un valor y
unidad, poseen dirección.
Ejemplo:
1) Velocidad: Un carro que se
desplaza hacia el Este con una
rapidez de 180 km/h.
2) Aceleración: Un cuerpo que
cae verticalmente, acelerando a
razón de 9,8 m/s2

12. Sistema Internacional de Unidades de Medida (S.I.)
A través de la historia, cada pueblo estableció su propio sistema
de pesas y medidas, algunas de las cuales todavía subsisten y otras
han dejado de usarse; sin embargo, las necesidades del
intercambio comercial y científico han llegado a unificar ciertas
unidades, formándose el Sistema Internacional de Unidades (S.I)
En la X Conferencia de Pesas y Medidas (1954) se establecieron las
unidades y magnitudes fundamentales del S.I. Este sistema fue
complementado en la XIV Conferencia (realizada en Francia en
1971).
El Sistema Internacional se ha establecido a partir de siete
magnitudes fundamentales y dos complementarias o
suplementarias.

13. a) Unidades de base
Son aquellas mediante las cuales todas
las otras unidades del SI se pueden
derivar. Están definidas a base de
fenómenos naturales invariables y son
consideradas mutuamente
independientes.

15. b) Unidades suplementarias
Son unidades de medida adimensionales que por sus
características muy particulares aún no han sido
clasificados dentro de las unidades de base, ni como
unidades derivadas

16. C) Unidades derivadas
Están expresadas algebraicamente
en función de las unidades de base y
las unidades suplementarias.
Algunas de estas unidades tienen
nombre y símbolo propio y pueden
ser utilizadas para expresar otras
unidades derivadas.

18. Notación científica
 Notación que permite expresar los números muy
grandes y las fracciones decimales sumamente
pequeñas en una forma abreviada usando potencias
de 10. Es la expresión breve de números con muchas
cifras, para ello se emplea la potencia de base 10.
 Ejemplo: 0,004 8 = 4,8x10-3

19. Notación científica de números grandes
Notación científica de fracciones
decimales muy pequeñas

20. Escritura correcta de las medidas en el
sistema internacional (S.I)
a) Cada unidad y símbolo tienen un nombre propio y se
escribe con letra minúscula. Solamente se escriben
con letra mayúscula el símbolo correspondiente a la
unidad que deriva de nombre de los científicos.
b) Entre el valor y la unidad física se debe dejar un
espacio.
c) El prefijo y la unidad se escriben juntos.

21. d) La multiplicación de dos unidades se lee tal como
se presenta, una a continuación de la otra.
Ejemplos:
20 N.m se lee: Veinte newton metro
80 W.h se lee: Ochenta watts hora
e) El cociente de dos unidades se lee intercalando
entre el nombre de las unidades con la palabra “por”
Ejemplos:
15 m/s se lee: Quince metros por segundo
9 N/C se lee: Nueve newton por coulomb

22. f) Los símbolos que corresponden a las unidades
físicas no se pluralizan.
Ejemplos:
Cuarenta y cinco metros = 45 m
Ochenta y nueve watts = 89 W
Dieciocho centímetros = 18 cm
g) El prefijo y la unidad física constituye una sola
palabra compuesta.
Ejemplos:
40 kW se lee: Cuarenta kilowatts
90 mC se lee: Noventa microcoulombs

23. Múltiplos y submúltiplos decimales del sistema internacional (S.I)

24. Ejercicios
1. Un cuadro rectangular mide 150 cm por
70 cm y se le pone un marco que cuesta
S/.7 el metro de marco. ¿Cuánto costará el
marco?
a) S/.15,4 b) S/.30 c) S/.6.6
d) S/.30,8 e) S/.308

25. 2. Un pozo de 400 cm de largo, 15 dm de
altura y 200 cm ancho contiene agua
totalmente lleno. ¿Cuántos litros de agua
hay en este pozo?
a) 6 000 b) 9 000 c) 12 000 d) 1 200
e) 7 500

26. 3. Un depósito se llena por tres llaves. Una
vierte 12 litros en cada 3 minutos, otra 5
daL en 20 minutos y la tercera 3 hL en cada
40 minutos. ¿Cuál será la capacidad del
depósito, si abriendo los tres grifos tarda
en llenarse 2,5 horas?
a) 864 L b) 25 920 L c) 210 L d) 2 100 L
e) 480 L

27. 4. ¿Cuánto costará pavimentar con
adoquines una calle rectangular de 80 m
de largo y 6 m de ancho, si cada adoquín
tienen una superficie de 24 cm2 y cuesta
S/.4?
a) S/.800 000 b) S/. 400 000 c) S/.800
d) S/.80 000 e) S/.40 000

28. 5. ¿Cuántos cm3 hay en 5×10-4 m3?
a) 0,5 cm3 b) 5 cm3 c) 500 cm3
d) 50 cm3 e) 25 cm3

29. 6. En una caja de 6 cm de ancho, 28 cm de
largo y 40 cm de altura, ¿Cuántos celulares
de 1,2 cm por 5,6 cm por 10 cm caben?

30. Física
Silvio Chávez Acevedo
Reloj atómico
más estable a
base de
entramado de
iterbio que
puede
mantenerse en
hora por 13 800
millones de
años, gracias a
10 mil átomos
que utiliza.

31. Mida las siguientes magnitudes, identifica el
instrumento, la unidad de medida y la respectiva
dimensión. Registra en la siguiente tabla:

32. La dimensión indica la naturaleza física de una magnitud.
Aunque una distancia se mida en unidades de pies o en
metros o en pulgadas, sigue siendo distancia, por que su
dimensión es longitud (L).
Para denotar la dimensión de una cantidad física se
utilizará corchete [ ].
DIMENSIÓN
Es una rama auxiliar de la física que estudia las relaciones
entre las cantidades fundamentales y derivadas. Tiene las
siguientes aplicaciones:
a) Relacionar una magnitud física con otras elegidas
como fundamentales.
b) Comprobar la veracidad de las fórmulas.
c) Elaborar fórmulas empíricas a partir de datos
experimentales.
ANÁLISIS DIMENSIONAL

33. a) La dimensión de los números, medidas angulares,
funciones trigonométricas y logaritmos es uno y se
denominan cantidades adimensionales.
Ejemplos:
[π] = 1; [60º] = 1; [sen30º] = 1; [log28] = 1
Reglas importantes
b) Las dimensiones se pueden tratar como cantidades
algebraicas; es decir, se pueden sumar y restar sólo si tienen
las mismas dimensiones; o sea, deben ser de la misma
naturaleza.
Ejemplo:
10 kg + 8 kg = 18 kg
M + M = M

34. Reglas importantes
c) Principio de homogeneidad.- Los términos en cada
lado de una ecuación deben tener las mismas dimensiones.
Si: AX2 + BY = CD, entonces: [AX2] =
[BY] = [CD], dimensionalmente todos los
términos de la ecuación son iguales.
Ejemplo: En la ecuación homogénea,
halla la fórmula dimensional de “X”. Si:
3AX + 4BC = 5E. Donde: A = aceleración y
E = velocidad.

35. Son aquellas relaciones de igualdad en donde
algunas magnitudes son conocidas y otras
desconocidas.
Ejemplo:
a) L3M2X - L3Y = L3M2T-1.
Incógnitas (cantidades físicas): X; Y
b) LmMnTs = L3M2mT3n-5m.
Incógnitas (números): m; n; s.
Ecuaciones dimensionales

36. Problemas
1. Halla las dimensiones de la siguientes magnitudes
derivadas más utilizadas:
a) Velocidad
b) Aceleración
c) Fuerza = masa  aceleración
d) Trabajo = fuerza  distancia
e) Potencia = trabajo/tiempo
f) Presión = fuerza/área
g) Densidad (r) = masa/volumen
h) Aceleración angular (a) = Dw/t
i) Carga eléctrica (q) = i.t
j) Campo eléctrico (E) = F/q
k) Potencial eléctrico (j) = W/q

37. 2. Halla las dimensiones de las siguientes constantes
físicas más conocidas.
a) G = constante de gravitación universal.
b) K = constante de Coulomb
c) R = constante universal de las gases.
t) h = constante de Planck, siendo h = 6,63 x 10-34 J.s

38. 3. Encuentre la fórmula dimensional de “K”. Si: U =
½.K.x2. Donde: U = Energía; x = longitud.
a) LMT-2 b) L2M c) L2MT-2 d) MT-2
e) L2MT-1

39. 4. ¿Qué magnitud representa Y, en: Y = 6.P.V; donde: P
= presión y V = volumen?
a) Fuerza b) Trabajo c) Potencia d) Masa e) Impulso

40. 5. Siendo la ecuación dimensionalmente correcta,
calcule la dimensión de “x” en:
Donde: f = frecuencia, d = distancia, A = área y m =
masa
a) M3L-3T-3 b) M3L-2T-3 c) M3L-3T-6
d) M3L-2T6 e) M3L-3T-6
f =
4 . .d A x
m
2


41. 6. Si la ecuación mostrada es dimensionalmente
correcta, siendo: v = velocidad, k = constante numérica.
¿Qué magnitud representa B?
a) Longitud b) aceleración c) masa d) velocidad
e) fuerza

42. 7. UNI 2003 II. En la ecuación . = P donde  es
densidad y P es presión, las dimensiones de la constante
 son:
a) L2T-4 b) L3 c) L2T-2 d) M2L2T-4 e) ML2T-2

43. 8. UNCP 2000 II. En la siguiente expresión, halla la
ecuación dimensional de: Z = E/B. Si: E = F.A.t y B =
m.a/t; donde: F = fuerza; A = superficie; m = masa; a =
aceleración; t = tiempo.
a) LT b) L2T-1 c) LT-2 d) L2T-2 e) L2T2

44. 9. UNI 2000 I. La posición X de una partícula en función
del tiempo “t” está dado por: X (t) = at2 - bt4 Con X en
metros y t en segundos. Las unidades de a y b,
respectivamente son:
a) m/s2 ; m/s4 b) m/s ; m/s2 c) m/s2 ; m/s
d) m/s4 ; m/s2 e) m2/s2 ; m/s4

45. 10. UNI 2004 I En la ecuación: AB + BC + AC = P2;
donde P es la presión, la dimensión del producto ABC
es…
a) M3L-3T-3 b) M3L-2T-3 c) M3L-3T-6
d) M3L-2T6 e) M3L-3T-6

46. 11. UNI 1994 II. Halla las dimensiones de C en la
expresión:
Donde: v = velocidad; m = masa; E = energía; T =
temperatura; P = potencia
a) L b) L c)  d) -1 e) M -1

47. 12. UNI 2011 II. Se ha determinado que la velocidad de un
fluido se puede expresar por la ecuación:
donde Pm es la presión manométrica del fluido e “Y” es
la altura del nivel del fluido. Si la ecuación es
dimensionalmente correcta, las magnitudes físicas de A
y B, respectivamente, son:
a) densidad y aceleración b) densidad y velocidad
c) presión y aceleración d) fuerza y densidad
e) presión y fuerza

48. 13. UNI 2013 II. La ecuación del movimiento de una
partícula es: ma + bv + kx = 0. Sea: y 2 = b/m,
donde: m = masa, a = aceleración, x = posición y v =
velocidad. Determine las dimensiones de /.
a) L b) LT-1 c) adimensional d) T-2 e) T