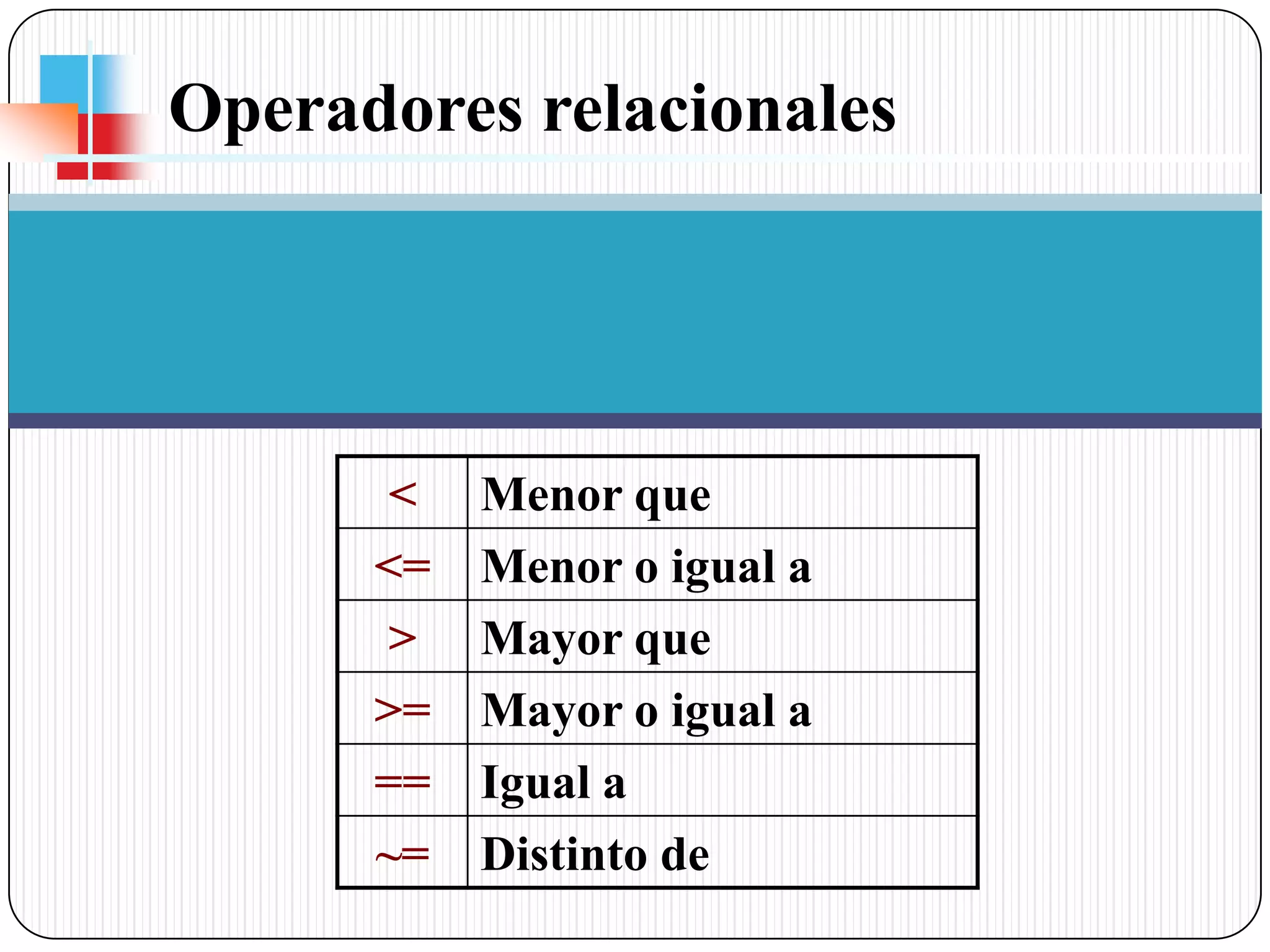
El documento describe las funciones básicas para manejar vectores y matrices en Matlab, incluyendo cómo definir, acceder y realizar operaciones con vectores y matrices, así como el uso del operador (:) y la función cat() para manipular submatrices. También cubre temas como matrices predefinidas, operadores relacionales y lógicos.

1. Manejo de Vectores y Matrices en Matlab

2. Definición de un vector Vector fila: elementos separados con comas (,) o con espacios: Vector columna: elementos separados con punto y coma (;) : Fila a columna y viceversa: con la transpuesta ( ´ ) Ejemplos a) desde línea de comandos, b) prog.: Vector columna Vector fila

3. El operador (:) El operador (:) es utilizado para especificar rangos, su forma de empleo es muy simple y sus beneficios inmensos. Forma de empleo: <vector>=[val_ini : paso : val_fin]; Ejemplo:

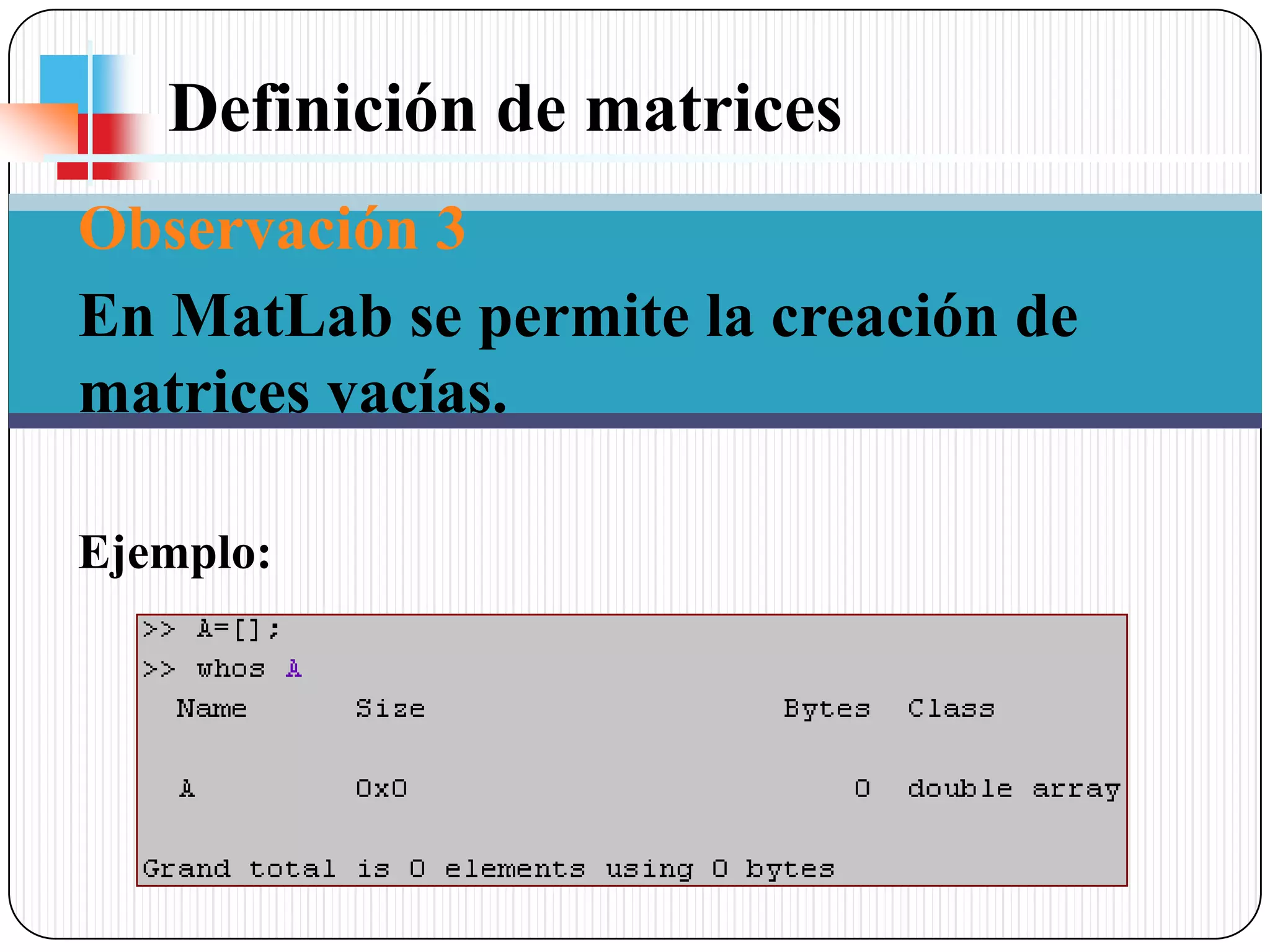
4. Definición de matrices Las matrices se definen por filas, los elementos de la fila se separan por espacios o comas (,) mientras que las filas van separadas por punto y coma (;) Ejemplos: A=[1,2,3; 4,5,6; 7,8,9] ó A=[1 2 3; 4 5 6; 7 8 9] Se ve en pantalla:

5. Definición de matrices Observación 1 Una vez definida la matriz esta pasa a su espacio de trabajo (Workspace) y estará disponible para realizarce cualquier operación. Ejemplo:

6. Definición de matrices Observación 2 MatLab introduce por defecto una variable llamada (ans) de “answer” sobre la cual también se puede operar. Ejemplo:

7. Definición de matrices Observación 3 En MatLab se permite la creación de matrices vacías. Ejemplo:

8. ¿Cómo acceder a los valores? Los elementos de una matriz se acceden poniendo los 2 índices entre paréntesis separados por coma (Ej. A(1,2)). Ejemplo:A(1,2)

9. ¿Cómo acceder a los valores? Observación 1 Si estamos trabajando con vectores bastaría colocar un solo índice. Ejemplo:

10. Operaciones VECTORES: A+B=[a1+b1 a2+b2 ... an+bn] A-B =[a1-b1 a2-b2 ... an-bn] A .* B=[a1.b1 a2.b2 ... an.bn] A y B deben ser horizontales o verticales. Si A=[fila] y B=[Columna]: Producto punto = A*B A./ B=[a1/b1 a2/b2 ... an/bn] A .^ n1=[a1^n1 a2^n1... an^n1 ] MATRICES: sin el punto A * B A/ B A ^ n1 Operaciones con escalares: v+k adición o suma v-k sustracción o resta v*k multiplicación v/k divide por k cada elemento de v k./v divide k por cada elemento de v v.^k potenciación cada componente de v esta elevado a k k.^v potenciación k elevado cada componente de v

14. Operaciones Ejemplo:

15. Matrices predefinidas

16. Operaciones con matrices Ejemplos:

17. El operador (:) El operador (:) se muestra mucho más potentecuando se trabaja con matrices.

18. El operador (:) Extracción de submatrices.

19. El operador (:) Extracción de una columna.

20. El operador (:) Extracción de una fila (end = última).

21. El operador (:) Eliminación de una columna.

22. La función (cat) La función (cat) se emplea para concatenar matrices a lo largo de una dimensión especificada. Al igual que el operador (:) es de una gran utilidad cuando se trabaja con matrices.

23. La función (cat) Ejemplo (1: abajo; 2: a la derecha): B C

24. Operadores relacionales

25. Operadores lógicos

26. Ejemplo de repaso: %Definición vector A=(1:2:11),B=(1:6) X=[3;6;7;12;1;5],Y=B' %operaciones con escalares C=A-2 D=3*Y-1 %operaciones entre vectores E=2*A+B F=A.*B G=Y./X H=X.^2 %definición de matrices I=[1 2 3 4;5 6 7 8;9 10 11 12] J=[5:8;8:11;11:14] K=zeros(4) L=ones(2,4) M=rand(4,4) %Manipulación de matrices N=I(2,3) %obtiene valor de la F2, C3 O=I(1:2,2:3) %extrae las primeras 2F y las cols 2 y 3 de I col1=I(:,1) % extrae la primera columna de la matriz union1=[L;K], union2=[I J] % unión de matrices %Operaciones con matrices sum=I+J mult=I*M pot=M^2 T=I.' deter=det(M) %Sistema de ecuaciones %Regla de Cramer Q=[1 2 3;2 3 4; 4 2 5] R=[4;5;1] D1=[R Q] D1=[4 2 3;5 3 4;1 2 5]; D2=[1 4 3;2 5 4;4 1 5]; D3=[1 2 4;2 3 5;4 2 1]; S=[det(D1),det(D2),det(D3)]/det(Q) %Inversa Q_inv=inv(Q) sol=Q_inv*R