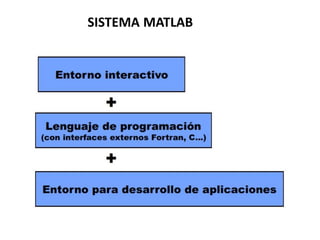
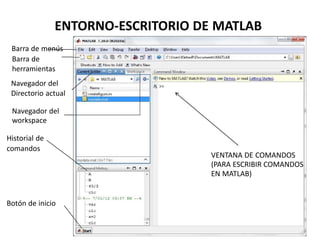
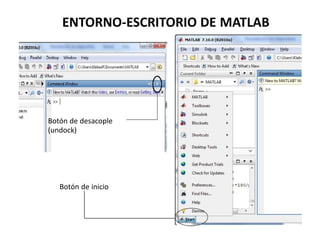
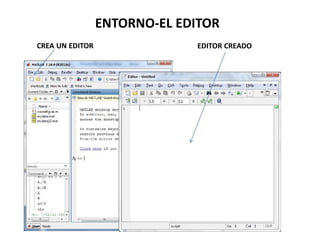
Este documento trata sobre los fundamentos de MATLAB. MATLAB es un lenguaje de programación técnica y de computación matricial. Ofrece múltiples herramientas para aplicar en diversas áreas como aeroespacial, biomédica, procesamiento de imágenes, entre otras. El documento explica los componentes básicos del sistema MATLAB, como la ventana de comandos y el entorno de escritorio. También cubre temas como vectores, matrices, operaciones numéricas y matriciales básicas.



![ENTORNO-WORKSPACE
Consiste en un conjunto de variables
(llamadas arreglos) construidas
durante una sesión de MATLAB y
almacenadas en memoria. Las
variables son añadidas al workspace
a través del uso de funciones,
ejecuciones de archivos M y
cargando Workspace almacenados
>> A=[9 8 7 6 5 4 3 2 1];
>> B=[6 7];
Todos los datos ingresados
al MATLAB son
almacenados en forma de
matriz o un arreglo
multidimensional](https://image.slidesharecdn.com/fundamentosdematlab-140726143504-phpapp02/85/Fundamentos-de-matlab-8-320.jpg)
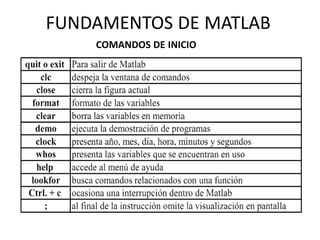











![size(A) : Devuelve el valor [número de filas, número de columnas] de la matriz A.
size(A,1) :
size(A,2) :
length(A) :
Devuelve el número de filas de la matriz A.
Devuelve el número de columnas de la matriz A.
Si A es un vector (fila o columna) devuelve el número de elementos
del vector.
Variablesmatriciales
Para crear una variable (o cambiar su valor) basta colocarla a la izquierda del
operador asignación (=). Podemos evaluar una expresión en MATLAB almacenando
el resultado en una variable.
variable = expresión
o simplemente para obtener el resultado
expresión
Cuyo valor se asigna a una variable interna llamada ans .
FUNDAMENTOS DE MATLAB
VECTORES Y MATRICES
Dimensionesde una matriz](https://image.slidesharecdn.com/fundamentosdematlab-140726143504-phpapp02/85/Fundamentos-de-matlab-24-320.jpg)



![>> A‘
ans =
1 4
2 5
3 6
7
8
9
>> B=A‘
B=
1 4
2 5
3 6
7
8
9
>> B*A
ans =
66 78 90
78 93 108
90 108 126
>> A=[1 2;3 4]
A=
1 2
3 4
>> A*2
ans =
2 4
6 8
>> A-4
ans =
-3 -2
-1 0
>> A/10
ans =
0.1000 0.2000
0.3000 0.4000
Recordar que el
resultado es una
matriz simétrica
FUNDAMENTOS DE MATLAB
VECTORES Y MATRICES
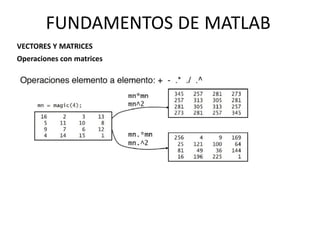
Operaciones con matrices
Ejercicios:](https://image.slidesharecdn.com/fundamentosdematlab-140726143504-phpapp02/85/Fundamentos-de-matlab-28-320.jpg)

![VECTORES Y MATRICES
Formas de construir matrices
[A1 A2 A3 …] ó horzcat(A1,A2,…)
Crea una matriz pegando las matrices A1,A2,… , (todas deben tener igual número de filas).
[A1;A2;A3 …] ó vertcat(A1,A2,…)
Crea una matriz apilando las matrices A1,A2,… , una debajo de otra (todas deben tener igual
número de columnas).
Juntando matrices
Usando funciones predefinidas
A’ : Devuelve la matriz transpuesta de A.
inv(A) : Devuelve la matriz inversa de A.
triu(A) : Devuelve la matriz triangular superior de la matriz A.
tril(A) : Devuelve la matriz triangular inferior de la matriz A.
diag(V) : Crea una matriz diagonal con el vector V en la diagonal.
diag(A) : Extrae la diagonal principal de la matriz A como vector columna.
eye(n) : Crea la matriz identidad de orden n.
eye(m,n) : Crea la matriz de tamaño mxn con unos en la diagonal principal y ceros en el resto.
FUNDAMENTOS DE MATLAB
toeplitz(v) define una matriz simétrica de diagonal constante con v como primera fila y
primera columna](https://image.slidesharecdn.com/fundamentosdematlab-140726143504-phpapp02/85/Fundamentos-de-matlab-31-320.jpg)

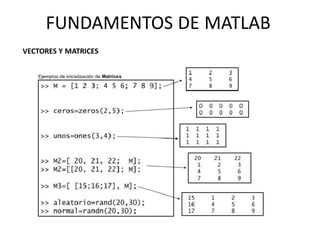
![VECTORES Y MATRICES
Formas de construir matrices
Usando funciones predefinidas
eye(size(A)) : Crea una matriz del mismo tamaño que A con unos en la diagonal principal
y ceros en el resto.
randi(imax,n) : Devuelve una matriz nxn con valores enteros pseudoaleatorios extraidos
de una distribución uniforme discreta en el intervalo (1:imax).
randi(imax,m,n) ó randi(imax,[m,n]) : Devuelve una matriz mxn con valores enteros
pseudoaleatorios extraidos de una distribución uniforme discreta en el intervalo (1:imax).
randi([imin imax],m,n) ó randi([imin imax],[m,n]) : Devuelve una matriz mxn con valores
enteros pseudoaleatorios extraidos de una distribución uniforme discreta en el intervalo
(imin:imax).
magic(n) : Devuelve una matriz nxn de enteros desde 1 hasta n^2 con igual suma de filas y
columnas. El orden de n debe ser un escalar mayor o igual a 3
FUNDAMENTOS DE MATLAB
randn(n) : Devuelve una matriz nxn con valores pseudoaleatorios extraidos de una
distribución normal (media 0 y varianza 1)](https://image.slidesharecdn.com/fundamentosdematlab-140726143504-phpapp02/85/Fundamentos-de-matlab-33-320.jpg)


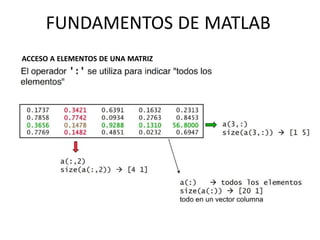

![VECTORES Y MATRICES
Formas de construir matrices
Indexando matrices a partir de vectores
V(J) ó V([j1 j2 j3 …]) : Devuelve el vector formado por los elementos de V indicados por J.
Es decir el vector [V(j1) V(j2) V(j3) … ]
A(I,:) ó A([i1 i2 i3 … ],:) : Define una matriz formada por la filas de A indicadas por I.
Es decir las filas i1-ésima,i2-ésima,etc. de A en ese orden.
A(:,J) ó A(:,[j1 j2 j3 … ]) : el mismo caso anterior para las columnas.
A(I,J) : Como en el caso anterior para elementos de esas filas y esas columnas.
A(m1:m2,:) : Define la submatriz de A formada por las filas entre la m1-ésima y la m2-ésima.
A(:,n1:n2) : Define la submatriz de A formada por las columnas entre la m1-ésima y la m2-
ésima.
A(m1:m2,n1:n2) : Devuelve la submatriz A formada por los elementos de las filas y las
columnas indicadas.
FUNDAMENTOS DE MATLAB](https://image.slidesharecdn.com/fundamentosdematlab-140726143504-phpapp02/85/Fundamentos-de-matlab-39-320.jpg)


![0.3517
1.0000
1.0000
0.5497
0.9172
0.2858
0.7572
0.7537
a=
0.1493 0.8143 0.1966 0.3517 0.9172
0 0 0 0 0.2858
0 0 0 0 0.7572
0.2543 0.3500 0.4733 0.5497 0.7537
>> a([2,3],[2,4])=ones(2,2)
a=
0.1493 0.8143 0.1966
0 1.0000 0
0 1.0000 0
0.2543 0.3500 0.4733
FUNDAMENTOS DE MATLAB
VECTORES Y MATRICES](https://image.slidesharecdn.com/fundamentosdematlab-140726143504-phpapp02/85/Fundamentos-de-matlab-42-320.jpg)

![Eliminar elementos dematrices
Asignando la matriz vacía “[]” , podemos eliminar el contenido de las variables:
V(I)=[] : Elimina los elementos del vector V indiciados por I. Devuelve el V resultante
A(I,:)=[] : Elimina las filas de la matriz A indiciadas por I .
A(:,J)=[] : Elimina las columnas de la matriz A indiciadas por J .
A(K)=[] : Elimina los elementos de A indiciados por K. Devuelve A como un vector fila .
A(I,J)=D : Sustituye los elementos de A indiciados con los vectores I y J, por los
elementos correspondientes de la matriz D. Las matrices A(I,J) y D deben ser del
mismo tamaño.
A(K)=D : Sustituye los elementos de A indiciados con la matriz K por los elementos
correspondientes de la matriz D, dicha indexación es por columnas.
Cambiar valores de matrices
FUNDAMENTOS DE MATLAB](https://image.slidesharecdn.com/fundamentosdematlab-140726143504-phpapp02/85/Fundamentos-de-matlab-44-320.jpg)


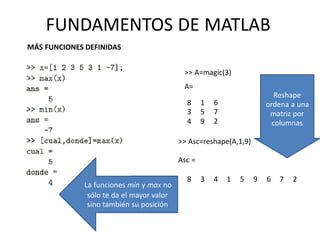




![>> x = [1 2 3]; y = [4 5 6];
>> cross (x,y) % producto
vectorial
ans =
-3 6 –3
>> dot (x,y) % producto
escalar
ans =
32
Estos conceptos
son my utilizados
para definir
magnitudes
física s
FUNDAMENTOS DE MATLAB
FUNCIONES PARA OPERAR CON VECTORES](https://image.slidesharecdn.com/fundamentosdematlab-140726143504-phpapp02/85/Fundamentos-de-matlab-52-320.jpg)


![-700
-1000
-300
-100
-300
-600
-600
-200
-500
700
-800
900
100 1000 -200 200 1000 800
800 -700 0 -500 500 700
400 700 -800 -400 -300 -500
-700 300 200 200 200 200
>> int8(A)
ans =
-128 -128 -128 -128 -128 -128
-128 -100 -128 -128 127 127
100 127 -128 127 127 127
127 -128 0 -128 127 127
127 127 -128 -128 -128 -128
-128 127 127 127 127 127
>> uint8(A)
ans =
0 0 0 0 0 0
0 0 0 0 255 255
100 255 0 200 255 255
255 0 0 0 255 255
255 255 0 0 0 0
0 255 200 200 200 200
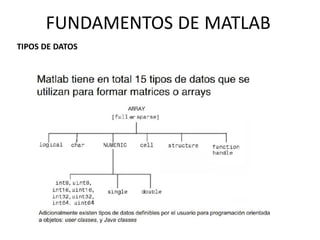
FUNDAMENTOS DE MATLAB
TIPOS DE DATOS
>> A=100*randi([-10 10],6)
A=](https://image.slidesharecdn.com/fundamentosdematlab-140726143504-phpapp02/85/Fundamentos-de-matlab-56-320.jpg)

![AttributesName Size Bytes Class
b 1x5 5 logical
FUNDAMENTOS DE MATLAB
TIPOS DE DATOS
TIPOS LÓGICOS
CREACIÓN DE UN ARREGLO LÓGICO
>> X=[true true false true false]
X=
1 1 0 1 0
>> whos X
Name Size Bytes Class Attributes
X 1x5 5 logical
>> a=[2.1 NaN 4.5 Inf 4];
>> b=isfinite(a)
b=
1 0 1 0 1
>> whos b](https://image.slidesharecdn.com/fundamentosdematlab-140726143504-phpapp02/85/Fundamentos-de-matlab-58-320.jpg)





![ESTRUCTURA Y CELL ARRAYS
>> c={12,'rojo',magic(4)}
c=
[12] 'rojo' [4x4 double]
>> d1{1}=12;
>> d1{2}='rojo';
>> d1{3}=magic(4);
>> d1
d1 =
[12] 'rojo' [4x4 double]
TIPOS DE DATOS
FUNDAMENTOS DE MATLAB
>> c={[true false true],[12.5 25 pi exp(1)],'verde',alumno}
c =
[1x3 logical] [1x4 double] 'verde' [1x1 struct]](https://image.slidesharecdn.com/fundamentosdematlab-140726143504-phpapp02/85/Fundamentos-de-matlab-64-320.jpg)
![ESTRUCTURA Y CELL ARRAYS
>> ss{1,1}=12;
>> ss{1,2}='rojo';
>> ss{1,3}=magic(4);
>> ss{2,1}=ones(3);
>> ss{2,2}=43;
>> ss{2,3}='texto';
>> ss
ss =
[ 12] 'rojo' [4x4 double]
[3x3 double] [ 43] 'texto'
TIPOS DE DATOS
FUNDAMENTOS DE MATLAB](https://image.slidesharecdn.com/fundamentosdematlab-140726143504-phpapp02/85/Fundamentos-de-matlab-65-320.jpg)








![>> A=[2 3 1 1;3 -2 -4 -3; 5 -1 -1 4]
A=
2 3 1 1
3 -2 -4 -3
5 -1 -1 4
>> rref(A)
ans =
1 0
0 1
0 1
0 -1
0 0 1 2
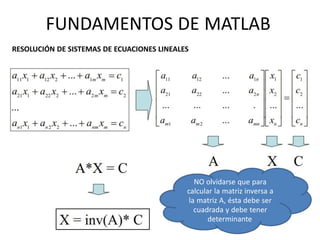
Ejercicio:
Obtener la solución al siguiente
sistema
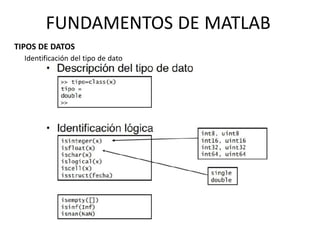
FUNDAMENTOS DE MATLAB
RESOLUCIÓN DE SISTEMAS DE ECUACIONES LINEALES](https://image.slidesharecdn.com/fundamentosdematlab-140726143504-phpapp02/85/Fundamentos-de-matlab-76-320.jpg)



