Este documento presenta un curso taller sobre el uso del editor científico LaTeX. El curso cubrirá instrucciones básicas de LaTeX, la estructura de documentos, la edición de texto y matemáticas, figuras y tablas, listas, bibliografías y los tipos de documentos más comunes. El objetivo del curso es proporcionar las herramientas básicas para crear composiciones en LaTeX, un formato estándar a nivel internacional.

1. Colegio de Matem´aticos del Per´u – Regi´on Piura Facultad de Ciencias – UNP
CURSO TALLER:
Herramientas del Editor Cient´ıfico LATEX
R. Ipanaqu´e 1
21 de marzo de 2014
1Profesor Asociado adscrito al Departamento Acad´emico de Matem´atica de la
Universidad Nacional de Piura.

3. Pr´ologo
En los ´ultimos cinco a˜nos, muchos de los eventos que se organizan a nivel
nacional requieren de la presentaci´on de trabajos en formato pdf los cuales
deben haberse generado mediante LATEX, lo que constituye una clara influencia
de colegas que han tenido la oportunidad de realizar estudios de post-grado en
el extranjero, pues, en eventos internacionales es obligatoria la presentaci´on de
trabajos generados con LATEX. Esto es algo saludable, ya que, no ser´ıa correcto
trabajar con software no estandarizado en una ´epoca en que se lucha por la
tan ansiada acreditaci´on universitaria.
Adem´as, cabe se˜nalar que con LATEX es sumamente pr´actico elaborar un
programa como plantilla (archivo de extensi´on cls, sty o simplemente tex) y
proporcionarlo, a los interesados en presentar sus trabajos en un determinado
evento, para que sea utilizado en la generaci´on de art´ıculos y as´ı obtener una
completa homogeneidad en todos los trabajos presentados.
Por otra parte la presentaci´on de los art´ıculos, reportes, libros, tesis, etc.
tienen un acabado profesional de alta calidad tipogr´afica cient´ıfica.
Por tales motivos se ha considerado la elaboraci´on de este curso taller:
Herramientas del Editor Cient´ıfico LATEX que pretende motivar y proporcionar
las herramientas b´asicas a los interesados en realizar sus composiciones en un
formato estandarizado a nivel internacional.
Robert Ipanaqu´e Chero
ripanaquec@unp.edu.pe
http://www.unp.edu.pe/pers/ripanaque
i

5. ´Indice general
1. Introducci´on 1
1.1. Distribuci´on LATEXy editor TEXMAKER . . . . . . . . . . . . . 1
1.2. Configuraci´on de TEXMAKER . . . . . . . . . . . . . . . . . . . 3
1.3. Instrucciones b´asicas de LATEX . . . . . . . . . . . . . . . . . . . 4
1.3.1. Comandos . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.3.2. Declaraciones globales (bloques) . . . . . . . . . . . . . . 4
1.3.3. Entornos . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.3.4. Comentarios . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.3.5. Espacios en blanco y saltos de l´ınea . . . . . . . . . . . . 5
1.3.6. S´ımbolos especiales . . . . . . . . . . . . . . . . . . . . . 5
1.4. Estructura de los documentos LATEX . . . . . . . . . . . . . . . . 6
1.4.1. Documentos b´asicos m´as utilizados . . . . . . . . . . . . 6
1.4.2. Estructura b´asica de un documento . . . . . . . . . . . . 6
1.5. Ejemplo de un documento LATEX . . . . . . . . . . . . . . . . . 7
2. Texto 11
2.1. Edici´on de texto . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
2.1.1. Tipos . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
2.1.2. Tama˜nos . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.2. Formato de texto . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.2.1. Texto centrado . . . . . . . . . . . . . . . . . . . . . . . 13
2.2.2. Alineaci´on a la izquierda o derecha . . . . . . . . . . . . 13
2.2.3. Citas textuales y poemas . . . . . . . . . . . . . . . . . . 14
2.2.4. Interlineado, sangr´ıa y espacios . . . . . . . . . . . . . . 15
2.2.5. Verbatim . . . . . . . . . . . . . . . . . . . . . . . . . . 16
2.2.6. Notas al pie de p´agina . . . . . . . . . . . . . . . . . . . 17
2.3. Texto, fondos y cajas en color . . . . . . . . . . . . . . . . . . . 18
2.4. Texto en columnas . . . . . . . . . . . . . . . . . . . . . . . . . 21
2.4.1. El paquete multicol . . . . . . . . . . . . . . . . . . . . 21
2.4.2. El entorno minipage . . . . . . . . . . . . . . . . . . . . 21
2.4.3. El comando parbox . . . . . . . . . . . . . . . . . . . . 22
2.5. L´ıneas y otros efectos de texto . . . . . . . . . . . . . . . . . . . 22
3. Matem´atica 24
3.1. Modos texto y display . . . . . . . . . . . . . . . . . . . . . . . 24
iii

6. iv ´INDICE GENERAL
3.2. Los comandos textstyle y displaystyle . . . . . . . . . . . 25
3.3. Construcciones diversas . . . . . . . . . . . . . . . . . . . . . . . 26
3.3.1. Fracciones . . . . . . . . . . . . . . . . . . . . . . . . . . 26
3.3.2. Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
3.3.3. Funciones a trozos . . . . . . . . . . . . . . . . . . . . . 27
3.3.4. Arriba y abajo . . . . . . . . . . . . . . . . . . . . . . . 27
3.3.5. Adornos y operadores . . . . . . . . . . . . . . . . . . . . 28
3.3.6. N´umeros combinatorios . . . . . . . . . . . . . . . . . . . 28
3.3.7. Fracciones generalizadas y continuas . . . . . . . . . . . 28
3.4. Texto en expresiones matem´aticas . . . . . . . . . . . . . . . . . 29
3.5. Tipos de letra en modo matem´atico . . . . . . . . . . . . . . . . 30
3.6. S´ımbolos matem´aticos en negrita . . . . . . . . . . . . . . . . . 30
3.7. Tama˜no de fuente en modo matem´atico . . . . . . . . . . . . . . 30
3.8. Alineaci´on de f´ormulas . . . . . . . . . . . . . . . . . . . . . . . 31
3.8.1. multline . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
3.8.2. gather . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
3.8.3. align . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
3.8.4. split . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
3.8.5. aligned . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
3.8.6. gathered . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
3.8.7. flalign . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
3.8.8. intertext . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
3.9. Par´entesis y signos de agrupaci´on . . . . . . . . . . . . . . . . . 38
3.10. Cajas de encuadre . . . . . . . . . . . . . . . . . . . . . . . . . 39
3.11. F´ormulas, fondos y cajas en color . . . . . . . . . . . . . . . . . 39
3.12. Teoremas y estructuras relacionadas . . . . . . . . . . . . . . . . 40
3.12.1. El paquete amsthm . . . . . . . . . . . . . . . . . . . . . 40
4. Figuras y tablas 50
4.1. El comando includegraphics . . . . . . . . . . . . . . . . . . 50
4.2. El entorno tabular . . . . . . . . . . . . . . . . . . . . . . . . . 51
4.3. Alineaci´on diferenciada en una columna . . . . . . . . . . . . . . 56
4.4. Divisi´on diagonal en celdas . . . . . . . . . . . . . . . . . . . . . 56
4.5. Rotando el texto de las celdas . . . . . . . . . . . . . . . . . . . 57
4.6. Escalamiento de tablas . . . . . . . . . . . . . . . . . . . . . . . 58
4.7. Especificar las dimensiones reales de una tabla . . . . . . . . . . 58
4.8. Tablas extensas . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
4.9. Color en tablas . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
4.9.1. Columnas en color . . . . . . . . . . . . . . . . . . . . . 60
4.9.2. Filas en color . . . . . . . . . . . . . . . . . . . . . . . . 61
4.9.3. Celdas individuales en color . . . . . . . . . . . . . . . . 62
4.10. Objetos flotantes . . . . . . . . . . . . . . . . . . . . . . . . . . 62
4.10.1. Creaci´on de figuras flotantes . . . . . . . . . . . . . . . . 63
4.10.2. Posicionamiento de figuras . . . . . . . . . . . . . . . . . 64

7. ´INDICE GENERAL v
4.10.3. Creaci´on de tablas flotantes . . . . . . . . . . . . . . . . 64
4.10.4. Posicionamiento de tablas . . . . . . . . . . . . . . . . . 65
4.11. El paquete subfigure . . . . . . . . . . . . . . . . . . . . . . . 65
5. Listas 67
5.1. Entorno enumerate . . . . . . . . . . . . . . . . . . . . . . . . . 67
5.2. Entorno itemize . . . . . . . . . . . . . . . . . . . . . . . . . . 68
5.3. Entorno description . . . . . . . . . . . . . . . . . . . . . . . 68
5.4. Entorno list . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
5.5. Listas anidadas . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
5.6. Manipulaci´on de etiquetas en el entorno enumerate . . . . . . . 72
5.7. Manipulaci´on de etiquetas en el entorno itemize . . . . . . . . 74
6. La bibliograf´ıa 75
6.1. El entorno thebibliography . . . . . . . . . . . . . . . . . . . 75
6.1.1. ´Indice de contenidos . . . . . . . . . . . . . . . . . . . . 76
6.2. El programa BibTEX . . . . . . . . . . . . . . . . . . . . . . . . 77
6.2.1. Estilos de BibTEX . . . . . . . . . . . . . . . . . . . . . 78
6.2.2. Pasos para ejecutar BibTEX con LATEX . . . . . . . . . . 78
6.2.3. Creaci´on de bases de datos bibliogr´aficos . . . . . . . . . 79
7. Documentos b´asicos 82
7.1. Art´ıculo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
7.2. Libro . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
7.3. Diapositivas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94
8. Elementos de programaci´on 100
8.1. Creaci´on de comandos y entornos . . . . . . . . . . . . . . . . . 100
8.1.1. Comandos . . . . . . . . . . . . . . . . . . . . . . . . . . 100
8.1.2. Entornos . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
8.2. Contadores y longitudes . . . . . . . . . . . . . . . . . . . . . . 104
8.2.1. Contadores . . . . . . . . . . . . . . . . . . . . . . . . . 104
8.3. Longitudes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108
8.3.1. Longitudes el´asticas fil . . . . . . . . . . . . . . . . . . . 112
9. Personalizaciones 116
9.1. El paquete titlesec . . . . . . . . . . . . . . . . . . . . . . . . 116
9.1.1. Resultado por defecto . . . . . . . . . . . . . . . . . . . 117
9.1.2. Personalizaci´on tesis fc-unp . . . . . . . . . . . . . . . . 117
9.1.3. Personalizaci´on titlerule . . . . . . . . . . . . . . . . . . 119
9.1.4. Personalizaci´on leftmarg . . . . . . . . . . . . . . . . . . 121
9.1.5. Personalizaci´on tikz . . . . . . . . . . . . . . . . . . . . . 123
9.2. El paquete facyhdr . . . . . . . . . . . . . . . . . . . . . . . . . 127
9.2.1. Resultado por defecto . . . . . . . . . . . . . . . . . . . 127
9.2.2. Personalizaci´on simple . . . . . . . . . . . . . . . . . . . 131

8. vi ´INDICE GENERAL
9.2.3. Personalizaci´on rule . . . . . . . . . . . . . . . . . . . . . 131
9.2.4. Personalizaci´on actualizable . . . . . . . . . . . . . . . . 134
9.3. El paquete titletoc . . . . . . . . . . . . . . . . . . . . . . . . 137
Bibliograf´ıa 140

9. Cap´ıtulo 1
Introducci´on
1.1. Distribuci´on LATEXy editor TEXMAKER
LATEX es un sistema de composici´on de textos; orientado especialmente a la
creaci´on de libros, documentos cient´ıficos y t´ecnicos que contengan f´ormulas
matem´aticas.
LATEX est´a formado por un gran conjunto de macros1
de TEX2
, escrito por
Leslie Lamport en 1984, con la intenci´on de facilitar el uso del lenguaje de
composici´on tipogr´afica TEX.
Una distribuci´on LATEX para Microsoft Windows es MiKTEX que fue desa-
rrollada por Christian Schenk y es libre. La ´ultima versi´on estable de MiKTEX
es la 2.9 que incluye el editor libre TEXworks, el cual es extremadamente sim-
ple, no obstante requiere de cierto dominio de c´odigo LATEX que naturalmente
no est´a al alcance de quien tiene un primer contacto con dicho sistema.
MiKTEX esta disponible en su p´agina oficial (ver Fig. 1.1)
http://miktex.org
1
Un macro –abreviatura de macroinstrucci´on– es una serie de instrucciones que se alma-
cenan para que se puedan ejecutar de manera secuencial mediante una sola llamada u orden
de ejecuci´on
2
TEX es un sistema de tipograf´ıa escrito por Donald E. Knuth (empezando a dise˜narlo
durante su a˜no sab´atico en 1978 y culminando la ´ultima versi´on estable alrededor de 1985),
muy popular en el entorno acad´emico, especialmente entre las comunidades de matem´aticos,
f´ısicos e inform´aticos
1

10. 2 CAP´ITULO 1. INTRODUCCI ´ON
Figura 1.1: Porci´on de la p´agina web oficialde MiKTEX.
Figura 1.2: Porci´on de la p´agina web oficialde TEXMAKER.
Un editor m´as mucho amigable que TEXworks es TEXMAKER. Dado que
TEXMAKER es un editor libre especialmente dise˜nado para hacer m´as f´acil y
c´omodo el trabajo con LATEX es que ha sido seleccionado para desarrollar este
curso taller.
TEXMAKER est´a est´a disponible en su p´agina oficial (ver Fig. 1.2)
http://www.xm1math.net/texmaker
La instalaci´on de MiKTEX y TEXMAKER se hace dando doble clic so-
bre el icono del respectivo instalador para luego seguir las instrucciones (se
recomienda usar los valores por defecto).

11. 1.2. CONFIGURACI ´ON DE TEXMAKER 3
1.2. Configuraci´on de TEXMAKER
Antes de empezar a elaborar cualquier documento en LATEX es preciso configu-
rar el editor TEXMAKER. Para ello deben efectuarse los siguientes pasos (ver
Fig. 1.3):
1. Acceder a TEXMAKER haciendo doble clic sobre el icono de acceso di-
recto que debe haberse creado en el escritorio.
2. Elegir <Configurar Texmaker> de la opci´on <Opciones> de la barra de
Men´u.
3. Seleccionar <Editor> de la ventana Configurar Texmaker y elegir ISO-
8859-1 en la opci´on Codificaci´on del editor. Elegir, adem´as, el diccionario
ES es.dic en la opci´on Diccionario. Aqu´ı es posible configurar: tipo y ta-
ma˜no de letra, colores para entorno matem´atico, comandos y palabras
clave, as´ı como los atajos.
4. Finalmente para que se actualicen las configuraciones se presiona el bot´on
<Aceptar> que se ubica en la parte inferior.
Figura 1.3: Configurando TEXMAKER.

12. 4 CAP´ITULO 1. INTRODUCCI ´ON
1.3. Instrucciones b´asicas de LATEX
1.3.1. Comandos
Los comandos de LATEX comienzan con seguido de una secuencia de letras3
.
Los diferentes tipos de comandos, as´ı como la sintaxis de los mismos son:
Simples4
:
<comando>
Con argumentos obligatorios:
<comando>{...}{...}...{...}
Con argumentos obligatorios y opcionales:
<comando>[<opcionales>]{...}{...}...{...}
1.3.2. Declaraciones globales (bloques)
Las declaraciones globales son aquellas que limitan su alcance al bloque de
texto contenido entre un par de llaves {...<texto>...} emparejadas.
1.3.3. Entornos
Los entornos son construcciones del documento que son tratadas de manera
distinta del documento principal, deben especificarse en la forma:
begin{<entorno>}
<texto>
end{<entorno>}
3
Los comandos en LATEX son sensibles a may´usculas y min´usculas.
4
Luego de los comandos simples los espacios son ignorados, por esta raz´on es im-
portante forzar a que aparezcan ´estos mediante cualquiera de las siguientes secuencias:
<comando> , {<comando>} o <comando>{}.

13. 1.3. INSTRUCCIONES B ´ASICAS DE LATEX 5
1.3.4. Comentarios
Todo texto que se encuentre a la derecha del s´ımbolo % no es procesado, de
esta forma se pueden agregar los comentarios dentro de un documento LATEX.
1.3.5. Espacios en blanco y saltos de l´ınea
En cuanto a los espacios en blanco y los saltos de l´ınea todo estudiante de
LATEX debe tener bien grabadas las siguientes siete reglas b´asicas:
1. Con muchos espacios en blanco que se agreguen entre palabras, LATEX
los considera como uno solo.
2. Para indicar el inicio de un nuevo p´arrafo es necesario pulsar la tecla
ENTER, con lo que se consigue dejar una l´ınea en blanco completa.
3. Por muchas l´ıneas en blanco completas que se agreguen entre dos p´arra-
fos, LATEX las trata como si s´olo hubiera una.
4. Si se quiere provocar un salto de l´ınea y permanecer en el mismo p´arrafo,
debe concluirse la l´ınea con uno de los siguientes comandos ,
[salto] o newline (donde el argumento opcional salto se refiere a
la distancia vertical adicional a la que debe situarse la siguiente l´ınea).
La versi´on * indica que la l´ınea que se inicia despu´es del comando no
debe pasar a la p´agina siguiente.
5. Si se quiere provocar un salto de l´ınea, permanecer en el mismo p´arrafo
y lograr la justificaci´on de la l´ınea abandonada, debe concluirse la l´ınea
con el comando linebreak.
6. Para provocar un salto de p´agina sin ajustar la p´agina abandonada, debe
concluirse el p´arrafo con el comando newpage.
7. Para provocar un salto de p´agina y lograr el ajuste de la p´agina aban-
donada, debe concluirse el p´arrafo con el comando pagebreak.
1.3.6. S´ımbolos especiales
Los siguientes s´ımbolos no se pueden obtener directamente, es necesario espe-
cificarlos mediante comandos: , {, }, $, etc. (Ver Cuad. 1.1)

14. 6 CAP´ITULO 1. INTRODUCCI ´ON
Cuadro 1.1: Tabla de s´ımbolos especiales m´as comunes.
S´ımbolo Comando S´ımbolo Comando
textbackslash & &
{ { } }
_ _ $ $
% % # #
^ ^ ~ ~
1.4. Estructura de los documentos LATEX
1.4.1. Documentos b´asicos m´as utilizados
article: para elaborar documentos cortos.
book: para elaborar documentos m´as extensos que contienen cap´ıtulos.
report: para elaborar informes t´ecnicos.
beamer: para elaborar dispositivas al estilo PowerPoint.
1.4.2. Estructura b´asica de un documento
La estructura b´asica de un documento es de la forma:
documentclass[<opciones>]{<clase>}
Pre´ambulo
<t´ıtulo>, <autor>, <fecha>
<declaraciones: paquetes>
begin{document}
Documento
<comandos especiales: maketitle>
<cuerpo del documento>
end{document}

15. 1.5. EJEMPLO DE UN DOCUMENTO LATEX 7
1.5. Ejemplo de un documento LATEX
Despu´es de haber accedido a TEXMAKER realizaremos los siguientes pasos:
1. Pulsar el bot´on <Nuevo> que se aprecia en la figura 1.4. Despu´es de esto
aparecer´a autom´aticamente una “hoja en blanco” como la que se aprecia
en la figura 1.5.
2. Elegir <Asistente para nuevo documento> de la opci´on <Asistentes> de
la barra de Men´u (ver Fig. 1.6), tras lo cual debe aparecer un cuadro de
di´alogo como el de la figura 1.75
.
3. Presionar el bot´on <Aceptar> ubicado en la parte inferior (ver Fig. 1.6).
Despu´es de esto, la hoja en blanco ser´a llenada autom´aticamente con el
c´odigo mostrado en la figura 1.8.
4. Escribir
maketitle ,
presionar ENTER y luego escribir
´Este es mi primer documento escrito en LaTeX.
en el campo ubicado entre begin{document} y end{document} (ver
Fig. 1.9).
5. Guardar el archivo (de preferencia en una nueva carpeta), asign´ando-
le un nombre. En nuestro caso convendremos en asignarle el nombre
ejemplo.tex.
6. Verificar que est´e activo el panel de mensajes presionando el bot´on
<Messages/Log>, ubicado en el extremo inferior izquierdo, hasta que
aparezca un cuadro como el que se aprecia en la parte inferior derecha
de la figura 1.10.
7. Presionar la tecla <F6> y esperar a que se compile el documento y se
genere el respectivo archivo pdf. Al finalizar la compilaci´on debe apare-
cer un mensaje (en el panel de mensajes) indicando que el proceso ha
terminado exitosamente (process exited normally).
8. Presionar la tecla <F7> para poder ver el archivo pdf con el visor de
TEXMAKER (ver Fig. 1.11).

16. 8 CAP´ITULO 1. INTRODUCCI ´ON
Figura 1.4: Bot´on <Nuevo> de la barra Archivo.
Figura 1.5: “Hoja en blanco” de TEXMAKER.
Figura 1.6: Opci´on asistente para nuevo documento.
Figura 1.7: Modelo para llenar el cuadro de di´alogo del asistente para nuevo
documento.

17. 1.5. EJEMPLO DE UN DOCUMENTO LATEX 9
Figura 1.8: “Hoja en blanco” llenada autom´aticamente.
Figura 1.9: Primer documento en LATEX.
Figura 1.10: Activando el panel de mensajes.

18. 10 CAP´ITULO 1. INTRODUCCI ´ON
Ejemplo
Robert Ipanaqu´e Chero
19 de Enero de 2014
´Este es mi primer documento escrito en LATEX.
1
Figura 1.11: Porci´on del Pdf del primer documento en LATEX.
Para realizar cualquier cambio en el documento simplemente se accede
al archivo tex (en este caso ejemplo.tex), se hace el cambio y se actualiza
presionado <F6> y luego <F7> (no olvide guardar los cambios. Una forma
r´apida de hacer esto es presionando la combinaci´on <Ctrl>+<S>).
T´engase presente que en la carpeta donde se ha almacenado el archivo, al
que se convino llamar ejemplo, se habr´an creado cuatro archivos. Espec´ıfica-
mente: ejemplo.tex, ejemplo.txt, ejemplo.aux y ejemplo.pdf.
5
El lector debe llenar los casilleros de autor y t´ıtulo; as´ı como seleccionar el tipo de do-
cumento (article), el tama˜no de letra (12pt), etc. y finalmente activar las casillas: Paquete
babel (con la opci´on spanish), Paquete geometry, etc.

19. Cap´ıtulo 2
Texto
2.1. Edici´on de texto
2.1.1. Tipos
LATEX elige el tama˜no y tipo de las fuentes usadas seg´un una estructura l´ogica.
Para cambiar directamente se pueden usar las instrucciones siguientes:
Comando Tipo
textrm{<texto>} Letra romana
textit{<texto>} Letra it´alica
texttt{<texto>} Letra typewriter
textbf{<texto>} Letra Negrita
textsf{<texto>} Letra sans serif
textsl{<texto>} Letra inclinada
textsc{<texto>} Letra vers´alita
Cada uno de los tipos de fuentes b´asicos tiene su modo enf´atico, el cual se
obtiene por medio de comando:
emph{<texto>}
A continuaci´on se muestra una tabla que contiene ejemplos acerca de los
resultados obtenidos al usar el modo enf´atico en los tipos de fuentes b´asicos.
11

20. 12 CAP´ITULO 2. TEXTO
El modo enf´atico El modo enf´atico
textrm{El modo enf´atico emph{El modo enf´atico}}
El modo enf´atico El modo enf´atico
textit{El modo enf´atico emph{El modo enf´atico}}
El modo enf´atico El modo enf´atico
texttt{El modo enf´atico emph{El modo enf´atico}}
El modo enf´atico El modo enf´atico
textbf{El modo enf´atico emph{El modo enf´atico}}
El modo enf´atico El modo enf´atico
textsf{El modo enf´atico emph{El modo enf´atico}}
El modo enf´atico El modo enf´atico
textsl{El modo enf´atico emph{El modo enf´atico}}
El modo enf´atico El modo enf´atico
textsc{El modo enf´atico emph{El modo enf´atico}}
Cabe mencionar que underline{subrayado} produce subrayado.
2.1.2. Tama˜nos
El tama˜no de la fuente depende de la selecci´on por defecto. Los comandos para
modificarlo son:
Comando Tama˜no
normalsize Letra normal
small Tama˜no normal
footnotesize Letra peque˜na
scriptsize Letra m´as peque˜na
tiny Letra muy peque˜na
large Letra grande
Large Letra m´as grande
LARGE Letra muy grande
huge Letra a´un m´as grande
Huge Letra enorme
Estos comandos afectan al texto que sigue a partir de su aparaci´on, o al
´area delimitada entre par´entesis. Por ejemplo:
Estas palabras aparecer´an en
{tiny letra peque~na}
Estas palabras aparecer´an en letra pe-
que˜na

21. 2.2. FORMATO DE TEXTO 13
Para ajustar autom´aticamente el espacio entre renglones, de acuerdo con
el tama˜no de letra en uso, se cuenta con el comando par. Un ejemplo de su
uso es el siguiente:
{Large ‘‘Todo saber tiene
de ciencia lo que tiene de
matem´atica’’, Poincar´e}
“Todo saber tiene de cien-
cia lo que tiene de ma-
tem´atica”, Poincar´e
{Large ‘‘Todo saber tiene
de ciencia lo que tiene de
matem´atica’’, Poincar´e par}
“Todo saber tiene de cien-
cia lo que tiene de ma-
tem´atica”, Poincar´e
2.2. Formato de texto
2.2.1. Texto centrado
El entorno center hace que el texto aparezca centrado. Si el texto fuera muy
largo, LATEXse ocupa de partirlo en varias l´ıneas, y si se quiere indicar el salto
de l´ınea se utiliza el comando .
begin{center} El ingenioso
hidalgo D. Quijote de la
Mancha end{center}
El ingenioso hidalgo
D. Quijote de la Mancha
2.2.2. Alineaci´on a la izquierda o derecha
De forma similar al entorno center existen los entornos flushright y flushleft
para alineaci´on del texto a derecha e izquierda, respectivamente.
begin{flushleft} Este texto
aparecer´a alineado por su
parte izquierda end{flushleft}
Este texto aparecer´a
alineado por su
parte izquierda
begin{flushright} Este texto
aparecer´a alineado por su
parte derecha end{flushright}
Este texto aparecer´a
alineado por su
parte derecha

22. 14 CAP´ITULO 2. TEXTO
2.2.3. Citas textuales y poemas
Existen otros entornos para resaltar partes de un texto, como citas textua-
les o poemas, de cierta longitud. Los entornos que nos permiten hacerlo son:
quote, quotation y verse. A continuaci´on se da una breve descripci´on de
estos entornos.
El entorno quote es adecuado para una cita textual no larga.
... B. Russell escribi´o:
begin{quote}
Las matem´aticas pueden ser definidas como aquel tema en el cual ni
sabemos nunca lo que decimos ni si lo que decimos es verdadero.
end{quote}
... B. Russell escribi´o:
Las matem´aticas pueden ser definidas como aquel tema en el cual
ni sabemos nunca lo que decimos ni si lo que decimos es verdadero.
El entorno quotation es m´as apropiado para citas largas. N´otese la diferen-
cia con respecto al anterior.
... W. Shakespeare utiliz´o la frase:
begin{quotation}
A veces, no es todo oro lo que reluce. En ocasiones, la palabra
sirve tambi´en para no decir la verdad; no, no es que se mienta,
simplemente, se dicen medias verdades, ¿o no?. La palabra, sin la
mirada, puede llegar a enga~nar; la mirada, sin siquiera la palabra,
no enga~na, ¿o si?. Nada es verdad ni es mentira, todo depende del
cristal con que se mira.
end{quotation}
... W. Shakespeare utiliz´o la frase:
A veces, no es todo oro lo que reluce. En ocasiones, la palabra
sirve tambi´en para no decir la verdad; no, no es que se mienta,
simplemente, se dicen medias verdades, ¿o no?. La palabra, sin la
mirada, puede llegar a enga˜nar; la mirada, sin siquiera la palabra,
no enga˜na, ¿o si?. Nada es verdad ni es mentira, todo depende del
cristal con que se mira.

23. 2.2. FORMATO DE TEXTO 15
Para escribir poes´ıa disponemos del entorno verse, donde cada verso es
separado con el comando .
He aqu´ı un poema:
begin{verse}
Voy a la casa donde no viviremos,
miro los muros que no levantar´an,
huelo las bugambilas que no crecer´an,
y con los hijos que jam´as tendremos,
salgo a ver el mar ...
donde se han hundido tantas cosa nuestras.
rightline{textsc{(M. Scorza)}}
end{verse}
He aqu´ı un poema:
Voy a la casa donde no viviremos,
miro los muros que no levantar´an,
huelo las bugambilas que no crecer´an,
y con los hijos que jam´as tendremos,
salgo a ver el mar ...
donde se han hundido tantas cosa nuestras.
(M. Scorza)
2.2.4. Interlineado, sangr´ıa y espacios
El espacio entre l´ıneas del texto se puede cambiar en el pre´ambulo con la orden:
renewcommand{baselinestretch}{<n´umero>}
donde n´umero se refiere a un factor de interlineado, que por defecto es 1. Por
ejemplo, si se pone:
renewcommand{baselinestretch}{2}
se estar´a escribiendo a doble espacio. Es posible fijar n´umero a un valor deci-
mal.

24. 16 CAP´ITULO 2. TEXTO
El espacio entre p´arrafos del texto se puede cambiar en el pre´ambulo con
la orden:
setlength{parskip}{<longitud>}
donde longitud se refiere a una medida. Por ejemplo si se pone:
setlength{parskip}{2cm}
se estar´a estableciendo un espacio de 2cm entre p´arrafos del texto. Aunque en
estos casos se sugiere usar:
setlength{parskip}{baselineskip}
Al inicio de un p´arrafo LATEXintroduce un sangrado de forma autom´atica,
que puede ser evitado con el comando noindent. La longitud del sangrado
del texto se puede cambiar en el pre´ambulo con la orden:
setlength{parindent}{<longitud>}
donde longitud se refiere a una medida, como en el caso previo.
Para aumentar la distancia entre p´arrafos pueden usarse los comandos
smallskip, medskip y bigskip, el ´ultimo de los cuales aproximadamente
supondr´ıa dejar una l´ınea en blanco, mientras que los otros se refieren a la
mitad y cuarta parte de ´este, respectivamente.
Para poner distancias entre palabras podemos usar alguno de los comandos
siguientes: (espacio entre palabras), quad (longitud de una M) y qquad
(longitud de dos M). Tambi´en se cuenta con los llamados micro-espacios que
son producidos por los comandos: , (un micro-espacio equivalente a un sexto
de un quad), ; (dos micro-espacios), : (tres micro-espacios) y ! (un micro-
espacio negativo).
2.2.5. Verbatim
En el ambiente verbatim, LATEX procesa el texto exactamente como est´a escrito
utilizando fuente typewriter. ´Util para secciones de c´odigo C, FORTRAN,
etc., ya que dentro de este ambiente los caracteres especiales de LATEX pierden
validez.

25. 2.2. FORMATO DE TEXTO 17
begin{verbatim}
c bucle en %i
do i=1, n
a(i,i+1) = i
end do
end{verbatim}
c bucle en %i
do i=1, n
a(i,i+1) = i
end do
Para obtener un texto corto en el modo verbatim se usa, por ejemplo
verb+verbatim breve+, lo que produce verbatim breve.
2.2.6. Notas al pie de p´agina
Las notas a pie de p´agina se generan con el comando
footnote{<texto de la nota>}
en la posici´on del texto en la que queremos que aparezca la marca de la nota.
El espacio entre entre el texto y el pie de p´agina se puede cambiar en el
pre´ambulo con la orden:
setlength{skipfootins}{<longitud>}
donde longitud se refiere a una medida. Por ejemplo si se pone:
setlength{skipfootins}{2cm}
se estar´a estableciendo un espacio de 2cm entre entre el texto y el pie de p´agina.
El espacio entre pies de p´agina se puede cambiar en el pre´ambulo con:
setlength{footnotesep}{<longitud>}
donde longitud se refiere a una medida, como en el caso previo.
La l´ınea que separa los pies de p´agina del texto tambi´en se puede cambiar.
El c´odigo que LATEX usa por defecto para elaborar dicha l´ınea es:

26. 18 CAP´ITULO 2. TEXTO
newcommand{footnoterule}{
vspace*{-3pt}noindentrule{2in}{0.4pt}vspace*{2.6pt}
}
Para modificar la l´ınea en cuesti´on escribimos, por ejemplo, en el pre´ambulo:
renewcommand{footnoterule}{
vspace*{-3pt}noindentrule{10in}{2pt}vspace*{2.6pt}
}
lo que aumentar´ıa el largo y grosor de dicha l´ınea (Note que al inicio del primer
c´odigo se usa newcommand, mientras que al inicio del segundo, renewcommand).
2.3. Texto, fondos y cajas en color
Es posible aplicar una caja a: texto, f´ormulas matem´aticas, elementos flotantes,
listas, entornos tipo center, flushleft, flushrigth y minipage.
Una forma sencilla de enmarcar un texto con una caja es usando el comando
fbox:
fbox{Texto enmarcado} Texto enmarcado
No obstante, para obtener texto, fondos y cajas en color es preciso usar el
paquete color. Esto se consigue escribiendo, en el pre´ambulo:
usepackage{color}
El color del texto se establece con el comando textcolor
textcolor{blue}{
Este texto est´a en azul} Este texto est´a en azul
El color del fondo de texto se establece con el comando colorbox.

27. 2.3. TEXTO, FONDOS Y CAJAS EN COLOR 19
colorbox{yellow}{
Este texto tiene fondo amarillo}
Este texto tiene fondo amarillo
Es posible combinar varios colores y elementos de fuente para lograr resul-
tados interesantes. Por ejemplo:
colorbox{yellow}{
textcolor{red}{
Texto en color rojo
y fondo amarillo}}
Texto en color rojo y fondo amarillo
Para incluir texto en una caja:
fcolorbox{red}{yellow}{
Una caja amarilla
con borde rojo}
Una caja amarilla con borde rojo
El grosor del borde es controlado por fboxrule. Vamos a establecer el
grosor del borde en 4 puntos:
setlength{fboxrule}{4pt}
fcolorbox{red}{white}{Una caja blanca con borde rojo
de 4pt de grosor}
Una caja blanca con borde rojo de 4pt de grosor
La separaci´on entre el borde y el objeto encerrado es controlado por fboxsep.
Vamos a establecer la separaci´on a cero:
setlength{fboxrule}{4pt}
setlength{fboxsep}{0pt}
fcolorbox{red}{white}{Una caja blanca con borde rojo
y separaci´on de 0pt}
Una caja blanca con borde rojo y separaci´on de 0pt

28. 20 CAP´ITULO 2. TEXTO
Modelo Especificaci´on Ejemplo
gray Un n´umero entre
0 y 1
definecolor{light-gray}{gray}{0.95}
rgb Tres n´umeros
entre 0 y 1
definecolor{orange}{rgb}{1,0.5,0}
RGB Tres n´umeros
entre 0 y 255
definecolor{orange}{RGB}{255,127,0}
HTML Seis n´umeros en
el sistema hexa-
decimal, similar
a los usados en
HTML
definecolor{orange}{HTML}{FF7F00}
cmyk cuatro n´umeros
entre 0 y 1
definecolor{orange}{cmyk}{0,0.5,1,0}
Cuadro 2.1: Modelos de color.
Aunque se pueden usar lo colores predefinidos (white, black, red, green,
blue, cyan, magenta o yellow), tambi´en es posible personalizar los colores.
Esto se consigue colocando en el pre´ambulo:
definecolor{nombre}{modelo}{especificaci´on}
donde nombre es el nombre que asignaremos al nuevo color; modelo es la forma
en que se describe el color y especificaci´on es la descripci´on del color (ver Cuad.
2.1).
Por ejemplo, poniendo en el pre´ambulo:
definecolor{miorange}{RGB}{234, 112, 2}
y usando el siguiente c´odigo:
setlength{fboxrule}{4pt}
setlength{fboxsep}{2pt}
fcolorbox{miorange}{yellow}{Una caja amarilla con borde naranja
y separaci´on de 2pt}
obtenemos:
Una caja amarilla con borde naranja y separaci´on de 2pt

29. 2.4. TEXTO EN COLUMNAS 21
2.4. Texto en columnas
2.4.1. El paquete multicol
La forma m´as sencilla es utilizar el paquete multicol, para ello se pone en el
pre´ambulo:
usepackage{multicol}
begin{multicols}{2}
Hace que el texto que est´a entre los delimitadores salga a
doble columna, LaTeX se encarga de manera autom´atica de
distribuir el texto entre las columnas de la mejor manera,
adem´as de acomodar el texto cuando hay un cambio de l´ınea.
El campo de separaci´on que se deja entre las columnas se
define en el pre´ambulo con la instrucci´on
verb@setlength{columnsep}{7mm}@, la cual dejar´ıa un
espacio de 7 mil´ımetros entre ellas.
end{multicols}
Hace que el texto que est´a entre los
delimitadores salga a doble columna,
LATEX se encarga de manera autom´ati-
ca de distribuir el texto entre las co-
lumnas de la mejor manera, adem´as
de acomodar el texto cuando hay un
cambio de l´ınea.
El campo de separaci´on que se
deja entre las columnas se defi-
ne en el pre´ambulo con la instruc-
ci´on setlength{columnsep}{7mm},
la cual dejar´ıa un espacio de 7 mil´ıme-
tros entre ellas.
2.4.2. El entorno minipage
Otra manera de insertar texto a doble columna (o m´as columnas), es utilizar
el entorno minipage.
begin{minipage}[t]{4cm}
Hace una mini p´agina de 4cm de ancho y con el texto ajustado
con la l´ınea superior (top).
end{minipage} hfill

30. 22 CAP´ITULO 2. TEXTO
begin{minipage}[t]{6cm}
Hace otra mini p´agina de 6cm de ancho y con el texto ajustado
con la l´ınea superior (top). Otras opciones de ajuste son:
bottom (b) y center (c).
end{minipage}
Hace una mini p´agina
de 4cm de ancho y con
el texto ajustado con
la l´ınea superior (top).
Hace otra mini p´agina de 6cm de
ancho y con el texto ajustado con
la l´ınea superior (top). Otras op-
ciones de ajuste son: bottom (b)
y center (c).
2.4.3. El comando parbox
Produce resultados similares a los obtenidos con minipage.
parbox[t]{4cm}{
Hace una caja de p´arrafos de 4cm de ancho y con el texto ajustado
con la l´ınea superior (top).} hfill
parbox[t]{6cm}{
Hace otra caja de p´arrafos de 6cm de ancho y con el texto ajustado
con la l´ınea superior (top). Otras opciones de ajuste son:
bottom (b) y center (c).}
Hace una caja de
p´arrafos de 4cm de
ancho y con el texto
ajustado con la l´ınea
superior (top).
Hace otra caja de p´arrafos de 6cm
de ancho y con el texto ajustado
con la l´ınea superior (top). Otras
opciones de ajuste son: bottom
(b) y center (c).
2.5. L´ıneas y otros efectos de texto
El comando hfill inserta un espacio tal que el texto que est´a despu´es del
mismo se alinea a la derecha.
Universidad Nacional de Piura hfill Tiempo: 2:00 hrs
Universidad Nacional de Piura Tiempo: 2:00 hrs

31. 2.5. L´INEAS Y OTROS EFECTOS DE TEXTO 23
El comando hrulefill inserta una l´ınea recta horizontal de modo que el
texto que est´a despu´es del mismo se alinea a la derecha.
Universidad Nacional de Piura hrulefill Tiempo: 2:00 hrs
Universidad Nacional de Piura Tiempo: 2:00 hrs
El comando dotfill inserta un puntos alineados horizontalmente de ma-
nera que el texto que est´a despu´es del mismo se alinea a la derecha.
Universidad Nacional de Piura dotfill Tiempo: 2:00 hrs
Universidad Nacional de Piura . . . . . . . . . . . . . . . . . . . . . . . . . . . . Tiempo: 2:00 hrs
El comando rule[dist]{ancho}{alto} dibuja una l´ınea recta horizontal o
vertical, donde dist es la distancia (puede ser negativa, nula o positiva) entre
la l´ınea y la base del texto, ancho es la longitud horizontal de la l´ınea y alto
es la longitud vertical de la misma.
Universidad Nacional de Piura hfill Tiempo: 2:00 hrs
rule[1cm]{textwidth}{0.01cm}
Universidad Nacional de Piura Tiempo: 2:00 hrs
El comando textwidth es una medida que equivale al ancho del texto en
la p´agina actual.

32. Cap´ıtulo 3
Matem´atica
3.1. Modos texto y display
LATEX divide la introducci´on de tipograf´ıa matem´atica seg´un se haga: en la
misma l´ınea del p´arrafo en que se est´a escribiendo (modo texto), o en p´arrafos
separados (modo display).
La tipograf´ıa matem´atica escrita en modo texto, ha de ser introducida en-
tre $ y $, mientras que para hacerlo en modo display, se encierra entre [ y
]. Adem´as, el entorno equation, que esencialmente tiene el mismo funcio-
namiento que [ y ], a˜nade adem´as un n´umero a la ecuaci´on para futuras
referencias. Por ejemplo:
Todo emph{n´umero real}
no negativo $x$ se
representa mediante una
fracci´on decimal infinita
[
lfloor xrfloor,x_1,x_2,ldots,
]
donde $lfloor xrfloor$ es el
n´umero entero mayor que no
sobrepasa $x$ y se denomina
emph{parte entera} del n´umero
$x$, $x_nin{1,2,ldots,9}$
para cualquier $ninmathbb{N}$.
Todo n´umero real no negativo x
se representa mediante una fracci´on
decimal infinita
x , x1, x2, . . . ,
donde x es el n´umero entero ma-
yor que no sobrepasa x y se deno-
mina parte entera del n´umero x,
xn ∈ {1, 2, . . . , 9} para cualquier
n ∈ N.
24

33. 3.2. LOS COMANDOS TEXTSTYLE Y DISPLAYSTYLE 25
3.2. Los comandos textstyle y displaystyle
Determinadas construcciones matem´aticas adquieren un tama˜no distinto seg´un
es escriban en modo texto o display. Por ejemplo:
La f´ormula $sum_{k=1}^{n}k =
frac{n(n+1)}{2}$ es bien
conocida.
La f´ormula n
k=1 k = n(n+1)
2
es bien
conocida.
La f´ormula [sum_{k=1}^{n}k =
frac{n(n+1)}{2}] es bien
conocida.
La f´ormula
n
k=1
k =
n(n + 1)
2
es bien conocida.
La primera ha sido escrita en modo texto y la segunda en modo display.
Si se quiere obtener resultados distintos en uno u otro modo debe usarse los
comandos textstyle (en modo display) o displaystyle (en modo texto).
As´ı:
La f´ormula $displaystyle
sum_{k=1}^{n}k =
frac{n(n+1)}{2}$ es bien
conocida.
La f´ormula
n
k=1
k =
n(n + 1)
2
es
bien conocida.
La f´ormula [textstyle
sum_{k=1}^{n}k =
frac{n(n+1)}{2}] es bien
conocida.
La f´ormula
n
k=1 k = n(n+1)
2
es bien conocida.

34. 26 CAP´ITULO 3. MATEM ´ATICA
3.3. Construcciones diversas
3.3.1. Fracciones
[
frac{frac{a}{x-y}+frac{b}{x+y}}
{1+frac{a-b}{a+b}}
]
a
x−y
+ b
x+y
1 + a−b
a+b
3.3.2. Matrices
[
left( begin{array}{lll}
1 & 2 & 3 4 & 5 & 6 7 & 8 & 9
end{array}right)
]


1 2 3
4 5 6
7 8 9


[
left( begin{array}{ccc}
1 & cdots & n 2 & cdots & n+1
vdots & ddots & vdots
n & cdots & 2n-1
end{array}right)
]





1 · · · n
2 · · · n + 1
...
...
...
n · · · 2n − 1





begin{equation}
begin{matrix} 0 & 11 & 0 end{matrix}qquad
begin{pmatrix} 0 & -ii & 0
end{pmatrix}qquad
begin{bmatrix} a & bc & d end{bmatrix}qquad
begin{vmatrix} 0 & 1-1 & 0
end{vmatrix}qquad
begin{Vmatrix} f & ge & v end{Vmatrix}
end{equation}
0 1
1 0
0 −i
i 0
a b
c d
0 1
−1 0
f g
e v
(3.1)

35. 3.3. CONSTRUCCIONES DIVERSAS 27
3.3.3. Funciones a trozos
[
psi(x)=begin{cases}
Ae^{ikx}+Be^{-ikx}, & text{si $x=0$,}
De^{- kx}, & text{si $xneq 0$.}
end{cases}
]
ψ(x) =
Aeikx
+ Be−ikx
, si x = 0,
De−kx
, si x = 0.
3.3.4. Arriba y abajo
[
astackrel{{rm def}}{=} alpha + betaquad
stackrel{beta to 0}{longrightarrow}
]
a
def
= α + β
β→0
−→
begin{equation*}
sum_{substack{0leq ileq m0>j>n}}phi(i,j)
end{equation*}
0≤i≤m
0>j>n
φ(i, j)
Observe, en el ´ultimo ejemplo, que el entorno alternativo equation* no
a˜nade ninguna numeraci´on a la ecuaci´on.
begin{equation*}
sum^{substack{0leq ileq m0>j>n}}phi(i,j)
end{equation*}

36. 28 CAP´ITULO 3. MATEM ´ATICA
0≤i≤m
0>j>n
φ(i, j)
3.3.5. Adornos y operadores
abc $widetilde{abc}$ abc $widehat{abc}$
←−
abc $overleftarrow{abc}$
−→
abc $overrightarrow{abc}$
abc $overline{abc}$ abc $underline{abc}$
abc $overbrace{abc}$ abc $underbrace{abc}$
√
abc $sqrt{abc}$ n
√
abc $sqrt[n]{abc}$
f $f^prime$ x $vec{x}$
3.3.6. N´umeros combinatorios
[
{n choose k} =
frac{n!}{k!,(n-k)!}
]
n
k
=
n!
k! (n − k)!
3.3.7. Fracciones generalizadas y continuas
El comando genfrac se puede utilizar para producir fracciones personaliza-
das, con la sintaxis:
genfrac{Delim.Izqdo}{Delim.Derecho}{GrosorL´ınea}
{Tama~no}{Numerador}{Denominador}
Para Tama˜no, se puede elegir entre los valores 0; 1; 2 y 3.
[
genfrac{{}{}}{0pt}{}{ij}{k}=
g^{k1}genfrac{[}{]}{0pt}{}{ij}{1}
+g^{k2}genfrac{[}{]}{0pt}{}{ij}{2}
]

37. 3.4. TEXTO EN EXPRESIONES MATEM ´ATICAS 29
ij
k
= gk1 ij
1
+ gk2 ij
2
Las fracciones continuas se obtienen a trav´es del comando cfrac.
[
frac{4}{pi} = 1+cfrac{1^2}{2+
cfrac{3^2}{2+cfrac{5^2}{2+dotsb}}}
]
4
π
= 1 +
12
2 +
32
2 +
52
2 + · · ·
3.4. Texto en expresiones matem´aticas
La instrucci´on text{texto} se usa para incluir texto en modo matem´atico.
´Este comando se utiliza principalmente en los despliegues, ya que en el discurso
corriente el modo matem´atico est´a delimitado por los s´ımbolos indicados en la
secci´on 3.1.
[
text{Para todo }varepsilon >0
text{ existe }delta >0
text{ tal que }|x-a|<delta
text{ implica }|f(a)-f(x)|<varepsilon.
]
Para todo ε > 0 existe δ > 0 tal que |x − a| < δ implica |f(a) − f(x)| < ε.

38. 30 CAP´ITULO 3. MATEM ´ATICA
3.5. Tipos de letra en modo matem´atico
$mathrm{abc...}$ abcd...
$mathrm{ABC...}$ ABCD...
$mathit{abc...}$ abcd...
$mathit{ABC...}$ ABCD...
$mathsf{abc...}$ abcd...
$mathsf{ABC...}$ ABCD...
$mathtt{abc...}$ abcd...
$mathtt{ABC...}$ ABCD...
$mathbf{abc...}$ abcd...
$mathbf{ABC...}$ ABCD...
$mathcal{ABC...}$ ABCD...
$mathfrak{abc...}$ abcd...
$mathfrak{ABC...}$ ABCD...
$mathbb{ABC...}$ ABCD...
3.6. S´ımbolos matem´aticos en negrita
El comando mathbf afecta solamente a las letras del alfabeto ordinario, a los
n´umeros y a las letras griegas may´uscula no inclinadas. El paquete amsmath
incluye el comando pmb (o boldsymbol) con los que se obtienen los s´ımbolos
matem´aticos en negrita.
[
text{Para todo } pmb{varepsilon} >0
text{ existe }pmb{delta} >0
text{ tal que }|x-a|<pmb{delta}text{ implica }
|f(a)-f(x)|<pmb{varepsilon}.
]
Para todo εεε > 0 existe δδδ > 0 tal que |x − a| < δδδ implica |f(a) − f(x)| < εεε.
3.7. Tama˜no de fuente en modo matem´atico
Para realizar el cambio del tama˜no del texto matem´atico se puede utilizar los
modificadores del texto normal, pero con la precauci´on de que el modificador
aplicado debe ser llamado antes de ingresar a un modo matem´atico.

39. 3.8. ALINEACI ´ON DE F ´ORMULAS 31
{tiny $f_x:Atomathbb{R}^2$} fx : A → R2
{small $f_x:Atomathbb{R}^2$} fx : A → R2
{Large $f_x:Atomathbb{R}^2$} fx : A → R2
{Huge $f_x:Atomathbb{R}^2$} fx : A → R2
3.8. Alineaci´on de f´ormulas
3.8.1. multline
begin{multline}
(a+b)^3 = (a+b)(a+b)(a+b)
= (a^2 + 2ab + b^2)(a+b)
= (a+b)(a^2 + 2ab + b^2)
= a^3 + 3a^2b + 3ab^2 + b^3
end{multline}
(a + b)3
= (a + b)(a + b)(a + b)
= (a2
+ 2ab + b2
)(a + b)
= (a + b)(a2
+ 2ab + b2
)
= a3
+ 3a2
b + 3ab2
+ b3
(3.2)
begin{multline*}
(a+b)^3 = (a+b)(a+b)(a+b)
= (a^2 + 2ab + b^2)(a+b)
= (a+b)(a^2 + 2ab + b^2)
= a^3 + 3a^2b + 3ab^2 + b^3
end{multline*}
(a + b)3
= (a + b)(a + b)(a + b)
= (a2
+ 2ab + b2
)(a + b)
= (a + b)(a2
+ 2ab + b2
)
= a3
+ 3a2
b + 3ab2
+ b3

40. 32 CAP´ITULO 3. MATEM ´ATICA
3.8.2. gather
begin{gather}
(a+b)^3 = (a+b)(a+b)(a+b)
= (a^2 + 2ab + b^2)(a+b)
= a^3 + 3a^2b + 3ab^2 + b^3
end{gather}
(a + b)3
= (a + b)(a + b)(a + b) (3.3)
= (a2
+ 2ab + b2
)(a + b) (3.4)
= a3
+ 3a2
b + 3ab2
+ b3
(3.5)
begin{gather}
(a+b)^3 = (a+b)(a+b)(a+b)
= (a^2 + 2ab + b^2)(a+b) notag
= (a+b)(a^2 + 2ab + b^2)
= a^3 + 3a^2b + 3ab^2 + b^3 notag
end{gather}
(a + b)3
= (a + b)(a + b)(a + b) (3.6)
= (a2
+ 2ab + b2
)(a + b)
= (a + b)(a2
+ 2ab + b2
) (3.7)
= a3
+ 3a2
b + 3ab2
+ b3
begin{gather*}
(a+b)^3 = (a+b)(a+b)(a+b)
= (a^2 + 2ab + b^2)(a+b)
= a^3 + 3a^2b + 3ab^2 + b^3
end{gather*}
(a + b)3
= (a + b)(a + b)(a + b)
= (a2
+ 2ab + b2
)(a + b)
= a3
+ 3a2
b + 3ab2
+ b3

41. 3.8. ALINEACI ´ON DE F ´ORMULAS 33
3.8.3. align
begin{align}
(a+b)^3 &= (a+b)(a+b)(a+b)
&= (a^2 + 2ab + b^2)(a+b)
&= (a+b)(a^2 + 2ab + b^2)
&= a^3 + 3a^2b + 3ab^2 + b^3
end{align}
(a + b)3
= (a + b)(a + b)(a + b) (3.8)
= (a2
+ 2ab + b2
)(a + b) (3.9)
= (a + b)(a2
+ 2ab + b2
) (3.10)
= a3
+ 3a2
b + 3ab2
+ b3
(3.11)
begin{align}
(a+b)^3 &= (a+b)(a+b)(a+b) notag
&= (a^2 + 2ab + b^2)(a+b)
&= (a+b)(a^2 + 2ab + b^2)
&= a^3 + 3a^2b + 3ab^2 + b^3 notag
end{align}
(a + b)3
= (a + b)(a + b)(a + b)
= (a2
+ 2ab + b2
)(a + b) (3.12)
= (a + b)(a2
+ 2ab + b2
) (3.13)
= a3
+ 3a2
b + 3ab2
+ b3
begin{align*}
(a+b)^3 &= (a+b)(a+b)(a+b)
&= (a^2 + 2ab + b^2)(a+b)
&= (a+b)(a^2 + 2ab + b^2)
&= a^3 + 3a^2b + 3ab^2 + b^3
end{align*}

42. 34 CAP´ITULO 3. MATEM ´ATICA
(a + b)3
= (a + b)(a + b)(a + b)
= (a2
+ 2ab + b2
)(a + b)
= (a + b)(a2
+ 2ab + b2
)
= a3
+ 3a2
b + 3ab2
+ b3
3.8.4. split
begin{equation}
begin{split}
(a+b)^3 &= (a+b)(a+b)(a+b)
&= (a^2 + 2ab + b^2)(a+b)
&= (a+b)(a^2 + 2ab + b^2)
&= a^3 + 3a^2b + 3ab^2 + b^3
end{split}
end{equation}
(a + b)3
= (a + b)(a + b)(a + b)
= (a2
+ 2ab + b2
)(a + b)
= (a + b)(a2
+ 2ab + b2
)
= a3
+ 3a2
b + 3ab2
+ b3
(3.14)
3.8.5. aligned
begin{equation}
begin{aligned}
a &= b + c + d
z &= x + y
m &= n
end{aligned}
qquad
begin{aligned}
A &= B + C + D
Z &= X + Y
end{aligned}
qquad

43. 3.8. ALINEACI ´ON DE F ´ORMULAS 35
begin{aligned}
phi &= mu +nu +eta
end{aligned}
end{equation}
a = b + c + d
z = x + y
m = n
A = B + C + D
Z = X + Y
φ = µ + ν + η (3.15)
begin{equation*}
begin{aligned}[t]
a &= b + c + d
z &= x + y
m &= n
end{aligned}
qquad
begin{aligned}[t]
phi &= mu +nu +eta
end{aligned}
end{equation*}
a = b + c + d
z = x + y
m = n
φ = µ + ν + η
3.8.6. gathered
begin{equation}
begin{gathered}[t]
a = b + c + d
z = x + y
m = n
end{gathered}
qquad
begin{gathered}[t]
A = B + C + D
Z = X + Y

44. 36 CAP´ITULO 3. MATEM ´ATICA
end{gathered}
qquad
begin{gathered}[t]
phi = mu +nu +eta
end{gathered}
end{equation}
a = b + c + d
z = x + y
m = n
A = B + C + D
Z = X + Y
φ = µ + ν + η (3.16)
begin{equation*}
begin{gathered}[b]
a = b + c + d
z = x + y
m = n
end{gathered}
qquad
begin{gathered}[b]
A = B + C + D
Z = X + Y
end{gathered}
qquad
begin{gathered}[b]
phi = mu +nu +eta
end{gathered}
end{equation*}
a = b + c + d
z = x + y
m = n
A = B + C + D
Z = X + Y φ = µ + ν + η
3.8.7. flalign
begin{flalign}
a &= b + c & A &= B + C & phi &= mu + nu + eta
z &= x + y & Z &= X + Y notag
m &= n

45. 3.8. ALINEACI ´ON DE F ´ORMULAS 37
end{flalign}
a = b + c A = B + C φ = µ + ν + η (3.17)
z = x + y Z = X + Y
m = n (3.18)
3.8.8. intertext
El comando intertext permite a˜nadir l´ıneas de texto en cualquiera de los
entornos de alineaci´on, de tal manera que se preserva la alineaci´on dada por
el entorno.
begin{align}
intertext{Dado que por la regla de la cadena se tiene la
igualdad}
(fg)^{prime} &= f^{prime}g + fg^{prime}
intertext{la cual se puede reescribir como}
fg^{prime} &= (fg)^{prime} - f^{prime}g
intertext{entonces se concluye que}
int fg^{prime} &= int (fg)^{prime} - int f^{prime}g
end{align}
Dado que por la regla de la cadena se tiene la igualdad
(fg) = f g + fg (3.19)
la cual se puede reescribir como
fg = (fg) − f g (3.20)
entonces se concluye que
fg = (fg) − f g (3.21)

46. 38 CAP´ITULO 3. MATEM ´ATICA
3.9. Par´entesis y signos de agrupaci´on
Para los s´ımbolos de los par´entesis y de los corchetes se usan las teclas usuales,
para los dem´as s´ımbolos LATEXprovee de una variada gama de comandos para
producir dichos signos de agrupaci´on. A continuaci´on se listan los comandos
de los signos m´as usualmente utilizados.
{ { } }
langle rangle
vert | Vert
lfloor rfloor
lceil rceil
Para aumentar el tama˜no de los s´ımbolos de agrupaci´on se usan los modi-
ficadores left y right antes del s´ımbolo. ´Estos se deben usar en pares, de
ser necesario, se usan los comandos left. o right. para formar el par.
Si los comandos left y right no producen los mejores resultados, pa-
ra esto, LATEXprovee los modificadores big, Big, bigg, Bigg, los cuales
permiten tener un mejor control sobre el tama˜no de los signos de agrupaci´on.
Adem´as de los modificadores anteriores el paquete amsmath provee una
versi´on mejorada de ´estos, en una versi´on de parejas de izquierda a derecha:
bigl bigr, Bigl Bigr, biggl biggr, Biggl Biggr.
$((a_1b_1)-(a_2b_2))((a_2b_1)+(a_1b_2))$
((a1b1) − (a2b2))((a2b1) + (a1b2))
$big((a_1b_1)-(a_2b_2)big)big((a_2b_1)+(a_1b_2)big)$
(a1b1) − (a2b2) (a2b1) + (a1b2)
$bigg((a_1b_1)-(a_2b_2)bigg)bigg((a_2b_1)+(a_1b_2)bigg)$
(a1b1) − (a2b2) (a2b1) + (a1b2)

47. 3.10. CAJAS DE ENCUADRE 39
$Big((a_1b_1)-(a_2b_2)Big)Big((a_2b_1)+(a_1b_2)Big)$
(a1b1) − (a2b2) (a2b1) + (a1b2)
$Bigg((a_1b_1)-(a_2b_2)Bigg)Bigg((a_2b_1)+(a_1b_2)Bigg)$
(a1b1) − (a2b2) (a2b1) + (a1b2)
3.10. Cajas de encuadre
A veces necesario disponer de este tipo de recuadros para controlar la altura
bajo una ra´ız, la alineaci´on de una f´ormula, etc.
Comando Descripci´on
phantom{XXX} espacio tan ancho y alto como tres X
hphantom{XXX} espacio tan ancho como tres X y altura 0
vphantom{XXX} espacio tan alto como tres X y ancho 0
Observe el efecto que produce el uso de vphantom{b} en la l´ınea horizontal
de
√
a en el siguiente ejemplo:
$sqrt{a}+sqrt{b}$
√
a +
√
b
$sqrt{vphantom{b}a}+sqrt{b}$
√
a +
√
b
3.11. F´ormulas, fondos y cajas en color
El proceso para generar f´ormulas, fondos y cajas en color es similar al que se
explica en la secci´on 2.3, la diferencia est´a en que las f´ormulas deben estar
delimitadas por $ y $.
fbox{$ax^2+bx+c=0,aneq 0$} ax2
+ bx + c = 0, a = 0

48. 40 CAP´ITULO 3. MATEM ´ATICA
textcolor{blue}{$ax^2+bx+c=0,aneq 0$} ax2
+ bx + c = 0, a = 0
[fcolorbox{red}{yellow}{
textcolor{blue}{$ax^2+bx+c=0,aneq 0$}}]
ax2
+ bx + c = 0, a = 0
setlength{fboxrule}{2pt}
setlength{fboxsep}{10pt}
[fcolorbox{red}{yellow}{
textcolor{blue}{$pmb{ax^2+bx+c=0,aneq 0}$}}]
ax2
+ bx + c = 0, a = 0ax2
+ bx + c = 0, a = 0ax2
+ bx + c = 0, a = 0
3.12. Teoremas y estructuras relacionadas
3.12.1. El paquete amsthm
El paquete amsthm incluye un conjunto de comandos que brindan mayor control
en la definici´on de las estructuras tratadas en esta secci´on. Este paquete se
invoca escribiendo en el pre´ambulo:
usepackage{amsthm}
El comando newtheorem
El comando
newtheorem{nombre}{r´otulo}[sub]
define una estructura numerada, creando el entorno nombre con su respectivo
contador. r´otulo aparece impreso cuando se invoca el entorno. La opci´on sub

49. 3.12. TEOREMAS Y ESTRUCTURAS RELACIONADAS 41
permite que las estructuras adquieran una numeraci´on subordinada respecto
de los cap´ıtulos, secciones, etc.
La forma
newtheorem{nombre}[principal]{r´otulo}
hace que la estructura nombre comparta la secuencia de numeraci´on con la
estructura principal.
El comando theoremstyle
La sintaxis de ´este comando es:
theoremstyle{estilo}
donde estilo puede ser:
plain Estilo por defecto de LATEX. Los r´otulos aparecen en negrita y el texto
enfatizado.
definition Los r´otulos aparecen en negrita pero el texto aparece en letra
normal.
remark Los r´otulo aparecen enfatizados y el texto aparece en letra normal.
El comando swapnumbers
´Este comando produce numeraci´on a izquierda en los entornos creados con
newtheorem (por ejemplo, 3.1. Teorema en vez de Teorema 3.1.).
El comando newtheorem*
´Este comando permite generar estructuras no numeradas.

50. 42 CAP´ITULO 3. MATEM ´ATICA
El entorno proof
La sintaxis de ´este entorno es:
begin{proof}[r´otulo]
. . .
end{proof}
y produce r´otulo (enfatizado) al principio de una demostraci´on, y el s´ımbolo
al final. Si se omite r´otulo, LATEX imprime Proof (o Demostraci´on si se usa
usepackage[spanish]{babel}).
El s´ımbolo puede ser reemplazado por otro cualquiera redefiniendo la
instrucci´on qedsymbol. As´ı por ejemplo, si el usuario prefiere el s´ımbolo
debe escribir en el pre´ambulo:
renewcommand{qedsymbol}{$blacksquare$}
El s´ımbolo para fin de demostraci´on aparece colocado en el ´ultimo rengl´on
del entorno proof, cargado a la derecha. Si el ´ultimo rengl´on es una f´ormula en
modo matem´atico independiente, el s´ımbolo aparece en una l´ınea nueva muy
abajo de la f´ormula. En tales situaciones se debe usar el comando qedhere
en el sitio preciso en el que finaliza la demostraci´on, antes de end{proof}.
Ejemplo de estructuras con numeraci´on no subordinada
documentclass{article}
...
usepackage{amsthm}
theoremstyle{definition}
newtheorem{midefinicion}{Definici´on}
newtheorem{miteorema}{Teorema}
newtheorem{micorolario}{Corolario}
newtheorem*{minota}{Nota}
...
begin{document}
...
begin{midefinicion}[L´ınea recta]
Llamamos l´ınea recta al lugar geom´etrico de los puntos tales
que tomados emph{dos puntos diferentes cualesquiera

51. 3.12. TEOREMAS Y ESTRUCTURAS RELACIONADAS 43
$P_{1}(x_{1},y_{1})$ y $P_{2}(x_{2},y_{2})$ del lugar},
el valor de la pendiente $m$ resulta siempre constante.
end{midefinicion}
begin{miteorema}[Forma punto-pendiente]
label{teo-ptom}
La recta que pasa por el punto dado $P_{1}(x_{1},y_{1})$ y tiene
la pendiente dada $m$, tiene por ecuaci´on
begin{equation}
label{eq-ptom}
y-y_{1} = m(x-x_{1}).
end{equation}
end{miteorema}
begin{micorolario}
La recta cuya pendiente es $m$ y cuya ordenada en el origen es $b$
tiene por ecuaci´on [y = mx+b.]
end{micorolario}
begin{miteorema}[Forma punto-punto]
La recta que pasa por dos puntos dados $P_{1}(x_{1},y_{1})$ y
$P_{2}(x_{2},y_{2})$ tiene por ecuaci´on
begin{equation}
label{eq-ptopto}
y-y_{1} = frac{y_{1}-y_{2}}{x_{1}-x_{2}}(x-x_{1}), ;
x_{1}neq x_{2}.
end{equation}
end{miteorema}
begin{proof}
Sea la recta $P_{1}P_{2}$. Como se conocen dos de sus puntos,
su pendiente est´a dada por
[m = frac{y_{1}-y_{2}}{x_{1}-x_{2}}, ; x_{1}neq x_{2}.]
Por tanto, con esta pendiente y el punto $P_{1}(x_{1},y_{1})$,
sustituyendo este valor de la pendiente en la ecuaci´on
(ref{eq-ptom}) del teorema ref{teo-ptom} obtenemos la forma
(ref{eq-ptopto}) tal como se quer´ıa demostrar.
end{proof}
begin{minota}
Si $x_{1}=x_{2}$ la ecuaci´on ref{eq-ptopto} no puede usarse.
En este caso la recta es paralela al eje $Y$, y su ecuaci´on es
$x=x_{1}$.

52. 44 CAP´ITULO 3. MATEM ´ATICA
end{minota}
...
end{document}
Definici´on 1 (L´ınea recta). Llamamos l´ınea recta al lugar geom´etrico de
los puntos tales que tomados dos puntos diferentes cualesquiera P1(x1, y1) y
P2(x2, y2) del lugar, el valor de la pendiente m resulta siempre constante.
Teorema 1 (Forma punto-pendiente). La recta que pasa por el punto dado
P1(x1, y1) y tiene la pendiente dada m, tiene por ecuaci´on
y − y1 = m(x − x1). (3.22)
Corolario 1. La recta cuya pendiente es m y cuya ordenada en el origen es b
tiene por ecuaci´on
y = mx + b.
Teorema 2 (Forma punto-punto). La recta que pasa por dos puntos dados
P1(x1, y1) y P2(x2, y2) tiene por ecuaci´on
y − y1 =
y1 − y2
x1 − x2
(x − x1), x1 = x2. (3.23)
Demostraci´on. Sea la recta P1P2. Como se conocen dos de sus puntos, su
pendiente est´a dada por
m =
y1 − y2
x1 − x2
, x1 = x2.
Por tanto, con esta pendiente y el punto P1(x1, y1), sustituyendo este valor
de la pendiente en la ecuaci´on (3.22) del teorema 1 obtenemos la forma (3.23)
tal como se quer´ıa demostrar.
Nota. Si x1 = x2 la ecuaci´on 3.23 no puede usarse. En este caso la recta es
paralela al eje Y , y su ecuaci´on es x = x1.
Ejemplo de estructuras con numeraci´on subordinada
documentclass{article}
...
usepackage{amsthm}
theoremstyle{definition}
newtheorem{midefinicion}{Definici´on}[section]

53. 3.12. TEOREMAS Y ESTRUCTURAS RELACIONADAS 45
newtheorem{miteorema}{Teorema}[section]
newtheorem{micorolario}{Corolario}[section]
newtheorem*{minota}{Nota}
...
begin{document}
...
begin{midefinicion}[L´ınea recta]
Llamamos l´ınea recta al lugar geom´etrico de los puntos tales
que tomados emph{dos puntos diferentes cualesquiera
$P_{1}(x_{1},y_{1})$ y $P_{2}(x_{2},y_{2})$ del lugar},
el valor de la pendiente $m$ resulta siempre constante.
end{midefinicion}
begin{miteorema}[Forma punto-pendiente]
label{teo-ptom}
La recta que pasa por el punto dado $P_{1}(x_{1},y_{1})$ y tiene
la pendiente dada $m$, tiene por ecuaci´on
begin{equation} label{eq-ptom}
y-y_{1} = m(x-x_{1}).
end{equation}
end{miteorema}
begin{micorolario}
La recta cuya pendiente es $m$ y cuya ordenada en el origen es $b$
tiene por ecuaci´on [y = mx+b.]
end{micorolario}
begin{miteorema}[Forma punto-punto]
La recta que pasa por dos puntos dados $P_{1}(x_{1},y_{1})$ y
$P_{2}(x_{2},y_{2})$ tiene por ecuaci´on
begin{equation} label{eq-ptopto}
y-y_{1} = frac{y_{1}-y_{2}}{x_{1}-x_{2}}(x-x_{1}), ;
x_{1}neq x_{2}.
end{equation}
end{miteorema}
begin{proof}
Sea la recta $P_{1}P_{2}$. Como se conocen dos de sus puntos,
su pendiente est´a dada por
[m = frac{y_{1}-y_{2}}{x_{1}-x_{2}}, ; x_{1}neq x_{2}.]
Por tanto, con esta pendiente y el punto $P_{1}(x_{1},y_{1})$,
sustituyendo este valor de la pendiente en la ecuaci´on
(ref{eq-ptom}) del teorema ref{teo-ptom} obtenemos la forma

54. 46 CAP´ITULO 3. MATEM ´ATICA
(ref{eq-ptopto}) tal como se quer´ıa demostrar.
end{proof}
begin{minota}
Si $x_{1}=x_{2}$ la ecuaci´on ref{eq-ptopto} no puede usarse.
En este caso la recta es paralela al eje $Y$, y su ecuaci´on es
$x=x_{1}$.
end{minota}
...
end{document}
Definici´on 3.12.1 (L´ınea recta). Llamamos l´ınea recta al lugar geom´etrico
de los puntos tales que tomados dos puntos diferentes cualesquiera P1(x1, y1)
y P2(x2, y2) del lugar, el valor de la pendiente m resulta siempre constante.
Teorema 3.12.1 (Forma punto-pendiente). La recta que pasa por el punto
dado P1(x1, y1) y tiene la pendiente dada m, tiene por ecuaci´on
y − y1 = m(x − x1). (3.24)
Corolario 3.12.1. La recta cuya pendiente es m y cuya ordenada en el origen
es b tiene por ecuaci´on
y = mx + b.
Teorema 3.12.2 (Forma punto-punto). La recta que pasa por dos puntos
dados P1(x1, y1) y P2(x2, y2) tiene por ecuaci´on
y − y1 =
y1 − y2
x1 − x2
(x − x1), x1 = x2. (3.25)
Demostraci´on. Sea la recta P1P2. Como se conocen dos de sus puntos, su
pendiente est´a dada por
m =
y1 − y2
x1 − x2
, x1 = x2.
Por tanto, con esta pendiente y el punto P1(x1, y1), sustituyendo este valor
de la pendiente en la ecuaci´on (3.24) del teorema 3.12.1 obtenemos la forma
(3.25) tal como se quer´ıa demostrar.
Nota. Si x1 = x2 la ecuaci´on 3.25 no puede usarse. En este caso la recta es
paralela al eje Y , y su ecuaci´on es x = x1.

55. 3.12. TEOREMAS Y ESTRUCTURAS RELACIONADAS 47
Ejemplo de estructuras con numeraci´on subordinada y compartida
documentclass{article}
...
usepackage{amsthm}
theoremstyle{definition}
swapnumbers
newtheorem{midefinicion}{Definici´on}[section]
newtheorem{miteorema}[midefinicion]{Teorema}
newtheorem{micorolario}[midefinicion]{Corolario}
newtheorem*{minota}{Nota}
renewcommand{qedsymbol}{$blacksquare$}
...
begin{document}
...
begin{midefinicion}[L´ınea recta]
Llamamos l´ınea recta al lugar geom´etrico de los puntos tales
que tomados emph{dos puntos diferentes cualesquiera
$P_{1}(x_{1},y_{1})$ y $P_{2}(x_{2},y_{2})$ del lugar},
el valor de la pendiente $m$ resulta siempre constante.
end{midefinicion}
begin{miteorema}[Forma punto-pendiente]
label{teo-ptom}
La recta que pasa por el punto dado $P_{1}(x_{1},y_{1})$ y tiene
la pendiente dada $m$, tiene por ecuaci´on
begin{equation} label{eq-ptom}
y-y_{1} = m(x-x_{1}).
end{equation}
end{miteorema}
begin{micorolario}
La recta cuya pendiente es $m$ y cuya ordenada en el origen es $b$
tiene por ecuaci´on [y = mx+b.]
end{micorolario}
begin{miteorema}[Forma punto-punto]
La recta que pasa por dos puntos dados $P_{1}(x_{1},y_{1})$ y
$P_{2}(x_{2},y_{2})$ tiene por ecuaci´on
begin{equation} label{eq-ptopto}
y-y_{1} = frac{y_{1}-y_{2}}{x_{1}-x_{2}}(x-x_{1}), ;
x_{1}neq x_{2}.

56. 48 CAP´ITULO 3. MATEM ´ATICA
end{equation}
end{miteorema}
begin{proof}
Sea la recta $P_{1}P_{2}$. Como se conocen dos de sus puntos,
su pendiente est´a dada por
[m = frac{y_{1}-y_{2}}{x_{1}-x_{2}}, ; x_{1}neq x_{2}.]
Por tanto, con esta pendiente y el punto $P_{1}(x_{1},y_{1})$,
sustituyendo este valor de la pendiente en la ecuaci´on
(ref{eq-ptom}) del teorema ref{teo-ptom} obtenemos la forma
(ref{eq-ptopto}) tal como se quer´ıa demostrar.
end{proof}
begin{minota}
Si $x_{1}=x_{2}$ la ecuaci´on ref{eq-ptopto} no puede usarse.
En este caso la recta es paralela al eje $Y$, y su ecuaci´on es
$x=x_{1}$.
end{minota}
...
end{document}
3.12.1 Definici´on (L´ınea recta). Llamamos l´ınea recta al lugar geom´etrico
de los puntos tales que tomados dos puntos diferentes cualesquiera P1(x1, y1)
y P2(x2, y2) del lugar, el valor de la pendiente m resulta siempre constante.
3.12.2 Teorema (Forma punto-pendiente). La recta que pasa por el punto
dado P1(x1, y1) y tiene la pendiente dada m, tiene por ecuaci´on
y − y1 = m(x − x1). (3.26)
3.12.3 Corolario. La recta cuya pendiente es m y cuya ordenada en el origen
es b tiene por ecuaci´on
y = mx + b.
3.12.4 Teorema (Forma punto-punto). La recta que pasa por dos puntos
dados P1(x1, y1) y P2(x2, y2) tiene por ecuaci´on
y − y1 =
y1 − y2
x1 − x2
(x − x1), x1 = x2. (3.27)
Demostraci´on. Sea la recta P1P2. Como se conocen dos de sus puntos, su
pendiente est´a dada por
m =
y1 − y2
x1 − x2
, x1 = x2.

57. 3.12. TEOREMAS Y ESTRUCTURAS RELACIONADAS 49
Por tanto, con esta pendiente y el punto P1(x1, y1), sustituyendo este valor
de la pendiente en la ecuaci´on (3.26) del teorema 3.12.2 obtenemos la forma
(3.27) tal como se quer´ıa demostrar.
Nota. Si x1 = x2 la ecuaci´on 3.27 no puede usarse. En este caso la recta es
paralela al eje Y , y su ecuaci´on es x = x1.

58. Cap´ıtulo 4
Figuras y tablas
4.1. El comando includegraphics
La sintaxis de este comando es:
includegraphics[<opciones>]{<nombre del archivo>}
Algunas de las opciones que incorpora este comando son:
width Anchura de la figura.
height Altura del figura.
scale Define un factor de escala a aplicar en ambas di-
recciones.
angle Especifica un ´angulo de rotaci´on en grados sexage-
simales.
viewport Define el trozo rectangular de la figura que se
quiere visualizar (Funciona s´olo con archivos pdf
y se usa en la forma viewport=xmin ymin xmax
ymax,clip).
includegraphics[width=2cm]{unp.png}
50

59. 4.2. EL ENTORNO TABULAR 51
includegraphics[width=2cm,height=1cm]{unp.png}
includegraphics[height=2cm,angle=45]{unp.png}
includegraphics[scale=0.17,angle=60]{unp.png}
includegraphics[scale=0.17,
angle=60]{fc.pdf}
includegraphics[
scale=1.75,
viewport=270 395 385 460,
clip]{fc.pdf}
4.2. El entorno tabular
La sintaxis de este comando es:
begin{tabular}[<pocisi´on>]{<colocaci´on>}
filas
end{tabular}

60. 52 CAP´ITULO 4. FIGURAS Y TABLAS
El significado de los argumentos es el siguiente:
posici´on Posici´on vertical de la tabla respecto de la l´ınea base. Puede tomar
los valores:
t la l´ınea superior de la tabla se alinea con la l´ınea base,
b la l´ınea inferior de la tabla se alinea con la l´ınea base,
Si no aparece el par´ametro, se centrar´a respecto de la l´ınea base.
colocaci´on Alineaci´on de las columnas. Debe aparecer una entrada por cada
columna de la tabla adem´as de entradas opcionales para delimitar los
bordes entre cada columna. Los formatos posibles para cada columna
son:
l alineaci´on a la izquierda,
c la columna aparecer´a centrada,
r alineaci´on a la derecha,
p{wd} elemento tipo p´arrafo. El texto aparecer´a en un p´arrafo de an-
chura wd, con la l´ınea superior alineada con las otras columnas.
*{num}{cols} abreviaci´on para repetici´on de formato. Por ejemplo, *{3}{c}
es equivalente a ccc.
Los elementos para separaci´on de columnas son:
| dibuja una l´ınea vertical,
| | dibuja dos l´ıneas verticales pr´oximas.
@{texto} inserta texto entre dos columnas. ´Util para cuando los valores de
una misma columna deben estar separados por una marca determinada
(gui´on, punto decimal, etc.) La expresi´on @{texto} elimina el espacio
autom´atico que se pone entre cada columna y lo sustituye por el texto.
Si se necesita espacio blanco extra, debe ser expl´ıcitamente incluido.
Cada una de las filas tendr´a la estructura siguiente:
elemento1 & elemento2 & ... & elementon
Es decir, el s´ımbolo & se utiliza para separar dos columnas consecutivas y el
comando para separar una fila de la siguiente. Todas las filas, salvo la ´ultima
debe ser finalizada con este comando.

61. 4.2. EL ENTORNO TABULAR 53
Otros comandos son:
hline este comando dibuja una l´ınea horizontal entre fila y fila. Debe apa-
recer s´olo antes de la primera fila, o justo a continuaci´on de . Dos
comandos hline dibujan dos l´ıneas con un peque˜no espacio entre ellas.
cline{n – m} como el comando hline, dibuja una l´ınea horizontal entre
la columna n hasta la columna m. S´olo se acepta que aparezca detr´as de
y puede haber m´as de uno.
vline este comando dibuja una l´ınea vertical en la l´ınea en la que aparece
de altura correspondiente a la fila en la que se encuentra.
multicolumn{n´umero}{col}{texto} engloba un n´umero de columnas dado
por n´umero bajo una columna simple cuya anchura corresponde a las
que engloba, con formato dado en col y con el contenido de texto.
begin{tabular}{|l|c|r|}
hline
uno & dos & tres
hline
cuatro & cinco & seis
hline
end{tabular}
uno dos tres
cuatro cinco seis
begin{tabular}{|l|c|r|}
hline
multicolumn{3}{|c|}{Tabla con
n´umeros}
hline
uno & dos & tres
hline hline
cuatro & cinco & seis
cline{1-2} siete & ocho & nueve
cline{2-3}
diez & once & doce
cline{1-3} trece &
multicolumn{2}{c|}{catorce}
hline
end{tabular}
Tabla con n´umeros
uno dos tres
cuatro cinco seis
siete ocho nueve
diez once doce
trece catorce

62. 54 CAP´ITULO 4. FIGURAS Y TABLAS
begin{tabular}{|lrrc|}
hline
Pa´ıs & Total & Ind´ıgenas & Porcentaje
hlinehline
Bolivia & 6,9 & 4,9 & 71
hline
Guatemala & 8,0 & 5,3 & 66
hline
Per´u & 20,0 & 9,3 & 47
hline
Ecuador & 9,5 & 4,15 & 43
hline
end{tabular}
Pa´ıs Total Ind´ıgenas Porcentaje
Bolivia 6,9 4,9 71
Guatemala 8,0 5,3 66
Per´u 20,0 9,3 47
Ecuador 9,5 4,15 43
begin{tabular}{|l|r@{,}l|r|}
hline
Estados Unidos & 14 & 7 & 10,5
hline
Italia & 1 & 82 & 0,25
hline
Francia & 3 & 4 & 0,6
hline
end{tabular}
Estados Unidos 14,7 10,5
Italia 1,82 0,25
Francia 3,4 0,6
begin{tabular}{|p{3cm}|{p4cm}|}
hline
Universidad Nacional de Piura & Facultad de Ciencias
hline
Colegio de Matem´aticos del Per´u & Curso Taller
hline
end{tabular}
Universidad Na-
cional de Piura
Facultad de Ciencias
Colegio de Ma-
tem´aticos del
Per´u
Curso Taller: “He-
rramientas del editor
cient´ıfico LATEX”

63. 4.2. EL ENTORNO TABULAR 55
El estilo de las tablas est´a definido por defecto por LATEX, y puede ser cam-
biado, globalmente en el pre´ambulo, o de forma local, no dentro del entorno.
Los par´ametros para realizar cambios de estilo en las tablas son:
tabcolsep corresponde a la mitad de la anchura del espacio insertado entre
dos columnas (valor por defecto: 6pt),
arrayrulewidth es el grosor de las l´ıneas que conforman la tabla (valor por
defecto: 0.4pt),
doublerulesep es la separaci´on entre las l´ıneas dobles (valor por defecto:
2pt),
arraystretch modifica la distancia entre las filas. Se trata de un factor mul-
tiplicativo, de modo que el valor est´andar corresponde a 1, y un valor de
1.5 aumenta un 50 % la distancia.
Para realizar modificaciones en estos par´ametros se usan las siguientes de-
claraciones:
setlengthtabcolsep{<dimensi´on>}
setlengtharrayrulewidth{<dimensi´on>}
setlengthdoublerulesep{<dimensi´on>}
renewcommand{arraystretch}{<factor>}
setlength{tabcolsep}{15pt}
setlength{arrayrulewidth}{2pt}
renewcommand{arraystretch}{3}
begin{tabular}{|l|c|r|}
hline
uno & dos & tres
hline
cuatro & cinco & seis
hline
end{tabular}
uno dos tres
cuatro cinco seis

64. 56 CAP´ITULO 4. FIGURAS Y TABLAS
4.3. Alineaci´on diferenciada en una columna
Si se necesita una alineaci´on particular para cada celda de una misma columna,
lo que podemos hacer es poner el texto dentro de una caja.
begin{tabular}{|l|l|}
hline
celda 1 &celda 2
hline
celda 3 &makebox[2.5cm][c]{celda 4}
hline
celda 5 &makebox[2.5cm][r]{celda 6}
hline
end{tabular}
celda 1 celda 2
celda 3 celda 4
celda 5 celda 6
4.4. Divisi´on diagonal en celdas
Para poder hacer divisiones diagonales en las tablas debemos usar el paquete
slashbox, por lo tanto debemos agregar en el pre´ambulo la declaraci´on:
usepackage{slashbox}
Cuando se quiere dividir una celda se usa el siguiente comando:
backslashbox{izq}{der}
donde izq y der ser´a el contenido de la celda a cada lado de la l´ınea diagonal.
begin{tabular}{|l|r|r|r|}
hline
backslashbox{origen}{destino} & Piura & Chiclayo & Trujillo
hline
Piura & 0 Km & 210 Km & 416 Km
hline
Chiclayo & 210 Km & 0 Km & 206 Km
hline
Trujillo & 416 Km & 206 Km & 0Km
hline
end{tabular}

65. 4.5. ROTANDO EL TEXTO DE LAS CELDAS 57
PPPPPPPPPorigen
destino
Piura Chiclayo Trujillo
Piura 0 Km 210 Km 416 Km
Chiclayo 210 Km 0 Km 206 Km
Trujillo 416 Km 206 Km 0Km
4.5. Rotando el texto de las celdas
Para rotar una tabla completa o simplemente el texto de una celda se usa el
entorno sideways del paquete rotating. Para ello se escribe en el pre´ambulo:
usepackage{rotating}
begin{sideways}
begin{tabular}{|l|r|r|}
hline
& columna 1 & columna 2
hline
fila 1 & $a_{11}$ & $a_{12}$
hline
fila 2 & $a_{21}$ & $a_{22}$
hline
end{tabular}
end{sideways}
columna1columna2
fila1a11a12
fila2a21a22
begin{tabular}{|l|r|r|}
hline
&begin{sideways}columna 1end{sideways}&
begin{sideways}columna 2end{sideways}
hline
fila 1 & $a_{11}$ & $a_{12}$
hline
fila 2 & $a_{21}$ & $a_{22}$
hline
end{tabular}
columna1
columna2
fila 1 a11 a12
fila 2 a21 a22

66. 58 CAP´ITULO 4. FIGURAS Y TABLAS
4.6. Escalamiento de tablas
Para escalar una tabla se usa el comando scalebox en la forma:
scalebox{escala horizonal}[escala vertical]{argumento}
scalebox{1.5}[2]{
begin{tabular}{|r|l|l|}
hline
&columna 1&columna 2
hline
fila 1& celda 1&celda 2
hline
fila 2& celda 3&celda 4
hline
end{tabular}}
columna 1 columna 2
fila 1 celda 1 celda 2
fila 2 celda 3 celda 4
scalebox{0.5}{
begin{tabular}{|r|l|l|}
hline
&columna 1&columna 2
hline
fila 1& celda 1&celda 2
hline
fila 2& celda 3&celda 4
hline
end{tabular}}
columna 1 columna 2
fila 1 celda 1 celda 2
fila 2 celda 3 celda 4
4.7. Especificar las dimensiones reales de una
tabla
Para escalar una tabla se usa el comando resizebox* en la forma:
resizebox*{ancho}{altura}{argumento}

67. 4.8. TABLAS EXTENSAS 59
resizebox*{3cm}{3cm}{
begin{tabular}{|r|l|l|}
hline
&columna 1&columna 2
hline
fila 1& celda 1&celda 2
hline
fila 2& celda 3&celda 4
hline
end{tabular}}
columna1 columna2
fila1 celda1 celda2
fila2 celda3 celda4
En el siguiente ejemplo solo se especifica la altura, y el ancho es calculado
de manera proporcional.
resizebox*{!}{2cm}{
begin{tabular}{|r|l|l|}
hline
&columna 1&columna 2
hline
fila 1& celda 1&celda 2
hline
fila 2& celda 3&celda 4
hline
end{tabular}}
columna 1 columna 2
fila 1 celda 1 celda 2
fila 2 celda 3 celda 4
4.8. Tablas extensas
Si una tabla es demasiado grande, una soluci´on es cortarla manualmente
y “reiniciarla” en la p´agina que sigue. La manera f´acil es usar el paquete
supertabular. Para usar este paquete ponemos en el pre´ambulo:
usepackage{supertabular}
begin{supertabular}{llll}
hline
Clave & C´odigo & Nombre del Curso & Insc
hline
3090 & CB2510 & Biolog´ıa Celular & 25
3035 & CB2410 & Bioqu´ımica & 39
3036 & CB2410 & Bioqu´ımica & 22

68. 60 CAP´ITULO 4. FIGURAS Y TABLAS
3020 & CB2405 & Bot´anica b´asica & 39
3080 & CB5308 & Desarrollo Ambiental & 21
3115 & CB4400 & Ecolog´ıa de Comunidades & 12
hline
end{supertabular}
Clave C´odigo Nombre del Curso Insc
3090 CB2510 Biolog´ıa Celular 25
3035 CB2410 Bioqu´ımica 39
3036 CB2410 Bioqu´ımica 22
3020 CB2405 Bot´anica b´asica 39
3080 CB5308 Desarrollo Ambiental 21
3115 CB4400 Ecolog´ıa de Comunidades 12
4.9. Color en tablas
Para poder colorear las tablas es posible usar el paquete colortbl, por lo tanto
cebe agregarse en el pre´ambulo:
usepackage{colortbl}
4.9.1. Columnas en color
Para colorear las columnas disponemos del comando columncolor. El modo
de usarlo es:
>{columncolor[modelo color]{color}}
definecolor{micolor}{rgb}{0,1,0.5}
begin{tabular}{|
>{columncolor[rgb]{0.7,0,0.7}}c |
>{columncolor[cmyk]{0.8,0.5,0.4,0.1}}c |
>{columncolor[gray]{0.7}}c |
>{columncolor{blue}}c |
>{columncolor{micolor}}c|}
hline
Col 1 & Col 2 & Col 3 & Col 4 & Col 5

69. 4.9. COLOR EN TABLAS 61
hline
rgb & cmyk & gray & predefinido & definido por nosotros
hline
end{tabular}
Col 1 Col 2 Col 3 Col 4 Col 5
rgb cmyk gray predefinido definido por nosotros
Para colorear el entorno multicolumn puede procedersecomo en el siguiente
ejemplo:
begin{tabular}{|c|c|}
hline
multicolumn{2}{|>{columncolor{red}}c|}{multicolumna 1-2}
hline
multicolumn{1}{|>{columncolor{green}}c|}{columna 1} &
multicolumn{1}{|>{columncolor{yellow}}c|}{columna 2}
hline
end{tabular}
multicolumna 1-2
columna 1 columna 2
4.9.2. Filas en color
La sintaxis es similar a la de las columnas, pero m´as sencilla:
rowcolor[model color]{color}
begin{tabular}{|l|l|}
hline
rowcolor[cmyk]{1,1,0,0}Abraham & Lapuerta
hline
rowcolor[rgb]{0,1,1}Roque & Fort
hline
rowcolor[gray]{0.9}Eva & Dirse
hline
end{tabular}

70. 62 CAP´ITULO 4. FIGURAS Y TABLAS
Abraham Lapuerta
Roque Fort
Eva Dirse
4.9.3. Celdas individuales en color
La sintaxis para colorear celdas individuales es la siguiente:
cellcolor[modelo color]{color}
begin{tabular}{|l|l|}
hline
cellcolor[cmyk]{1,1,0,0}Abraham & cellcolor{red}Lapuerta
hline
cellcolor[rgb]{0,1,1}Roque & cellcolor{blue}Fort
hline
cellcolor[gray]{0.9}Eva & cellcolor{green}Dirse
hline
end{tabular}
Abraham Lapuerta
Roque Fort
Eva Dirse
4.10. Objetos flotantes
La inclusi´on de figuras y tablas puede presentar problemas al intentar ubicarlas
en el texto pues al no poder ser divididas no pueden aparecer en cualquier punto
del documento. Para resolver este problema, es necesario tratar este tipo de
objetos como objetos flotantes1
, que son situados donde el compilador estima
conveniente.
1
Una forma sencilla de ilustrar un objeto flotante, por ejemplo una figura flotante, es
el siguiente: piense en una persona que redacta el texto de un documento y llega a un
punto, en un determinado p´arrafo, en el que precisa insertar una figura. Esta persona puede
escribir, por ejemplo, “... este proceso se ilustra en la siguiente figura:” y a continuaci´on de
este p´arrafo deber´a insertar la respectiva figura (no tiene otra opci´on). O puede escribir,
siguiendo con el mismo ejemplo, “... este proceso se ilustra en la figura n”. En este ´ultimo
caso, la persona del ejemplo, puede elegir entre insertar la figura a continuaci´on de este
p´arrafo; o insertarla uno, dos, etc. p´arrafos antes de este p´arrafo; o insertarla uno, dos, etc.
p´arrafos despu´es de este p´arrafo, siempre y cuando le asigne el n´umero n a la figura. Dado

71. 4.10. OBJETOS FLOTANTES 63
4.10.1. Creaci´on de figuras flotantes
Las figuras flotantes se crean con el entorno figure, en cuyo interior situamos
el correspondiente figura con includegraphics. La sintaxis del entorno es:
begin{figure}[<posici´on>]
centering
includegraphics{figura}
caption{<pie de la figura>}
label{<etiqueta>}
end{figure}
Los comandos caption y label son opcionales y sirven para situar
una leyenda para la figura, que aparecer´a numerada. Dicha numeraci´on
se asignar´a a la etiqueta label. El comando label debe ser situado
inmediatamente despu´es del caption.
Si el comando caption se crea una figura sin enumerar.
El comando listoffigures (normalmente situado al inicio del docu-
mento) genera una lista con todas las figuras incluidas en el documento.
El comando caption puede llevar un argumento opcional que especifica
el texto que aparecer´a en la Lista de Figuras. En caso de no aparecer,
dicho texto es el mismo que el argumento obligatorio del comando.
La figura flotante 4.1 ha sido creada con el siguiente c´odigo:
begin{figure}
centering
includegraphics[scale=0.25]{unp.png}
caption{Ejemplo de figura flotante.}
label{ej}
end{figure}
que la mencionada figura no necesariamente quedar´a ubicada inmediatamente despu´es del
p´arrafo, sino que flota en el documento, recibe el nombre de figura flotante (un ejemplo
similar se puede plantear para una tabla o cuadro). La ventaja aqu´ı es que LATEX ubica la
figura y le asigna un n´umero en forma autom´atica.

72. 64 CAP´ITULO 4. FIGURAS Y TABLAS
Figura 4.1: Ejemplo de figura flotante.
4.10.2. Posicionamiento de figuras
La posici´on en la que la figura aparece en el texto est´a determinada por el
argumento opcional que puede ser una (o m´as de una) de las siguientes letras
h, t, b, p.
h Sit´ua la figura all´ı donde aparece el entorno. Es-
ta opci´on no puede ser ejecutada siempre, pues
es posible que el figura no entre en el espacio
de p´agina que reste.
t Sit´ua la figura en la parte superior de la p´agina.
b Sit´ua la figura en la parte inferior de la p´agina.
p Sit´ua la figura en una p´agina separada.
Si no se especifica la posici´on, el compilador toma por defecto la secuencia
[tbp].
4.10.3. Creaci´on de tablas flotantes
Para tratar las tablas como un objeto flotante disponemos del entorno table,
cuya sintaxis es:
begin{table}[<posici´on>]
centering
entorno tabular
caption{<pie de la tabla>}
label{<etiqueta>}
end{table}

73. 4.11. EL PAQUETE SUBFIGURE 65
an
1 2 3
1 1 1 1
2 2 4 8
3 3 9 27
4 4 16 64
Cuadro 4.1: Potencias
Por ejemplo, la tabla 4.1 ha sido generada con el siguiente c´odigo:
begin{table}
centering
begin{tabular}{|l||c|c|l|}
hline
$a^n$ & 1 & 2 & 3
hlinehline
1 & 1 & 1 & 1cline{2-4}
2 & 2 & 4 & 8cline{2-4}
3 & 3 & 9 & 27cline{2-4}
4 & 4 & 16 & 64hline
end{tabular}
caption{Potencias}
label{ejt}
end{table}
4.10.4. Posicionamiento de tablas
Se usan los mismos argumentos opcionales que para el posicionamiento de
figuras (ver Subsec. 4.10.2).
4.11. El paquete subfigure
El paquete subfigure permite introducir subfiguras de manera f´acil. Para
utilizarlo debe colocarse en el pre´ambulo:
usepackage{subfigure}
Por ejemplo, la figura 4.2 se ha creado con el c´odigo:

74. 66 CAP´ITULO 4. FIGURAS Y TABLAS
begin{figure}
centering
subfigure[Logo del COMAP]{
qquadincludegraphics[scale=0.25]{logo.png}qquad}
subfigure[Logo de la FC]{
qquadincludegraphics[scale=0.15]{fc.png}qquad}
caption{Subfiguras.}
label{ej2}
end{figure}
(a) Logo del COMAP. (b) Logo de la FC.
Figura 4.2: Subfiguras.

75. Cap´ıtulo 5
Listas
Existen cuatro tipos de entornos para crear listas:
begin{enumerate} texto listado end{enumerate}
begin{itemize} texto listado end{itemize}
begin{description} texto listado end{description}
begin{list} texto listado end{list}
5.1. Entorno enumerate
begin{enumerate}
item Se trata de listas secuenciadas num´ericamente.
item Los n´umeros son consecutivos comenzando por 1,
en cada llamada al entorno.
end{enumerate}
1. Se trata de listas secuenciadas num´ericamente.
2. Los n´umeros son consecutivos comenzando por 1, en cada llamada al
entorno.
begin{enumerate}
addtocounter{enumi}{5}
67

76. 68 CAP´ITULO 5. LISTAS
item Es posible inicializar la numeraci´on a partir de
un n´umero diferente de 1 utilizando el comando
addtocounter.
item Por ejemplo, aqu´ı se inicializa la numeraci´on a
partir de 6.
end{enumerate}
6. Es posible inicializar la numeraci´on a partir de un n´umero diferente de
1 utilizando el comando addtocounter.
7. Por ejemplo, aqu´ı se inicializa la numeraci´on a partir de 6.
5.2. Entorno itemize
begin{itemize}
item Cada uno de los emph{items} son indicados con un
s´ımbolo determinado.
item La longitud del texto no tiene l´ımite.
end{itemize}
Cada uno de los items son indicados con un s´ımbolo determinado.
La longitud del texto no tiene l´ımite.
5.3. Entorno description
begin{description}
item[Primero:] Parece claro el funcionamiento de este
entorno.
item[Observaci´on:] No es un entorno demasiado frecuente.
end{description}
Primero: Parece claro el funcionamiento de este entorno.
Observaci´on: No es un entorno demasiado frecuente.

77. 5.4. ENTORNO LIST 69
5.4. Entorno list
El entorno list permite crear listas propias.
begin{list}{$clubsuit$}{}
item Colegio de Matem´aticos del Per´u -- Regi´on Piura.
item Facultad de Ciencias.
item Curso Taller: Herramientas del Editor Cient´ıfico LaTeX.
end{list}
♣ Colegio de Matem´aticos del Per´u – Regi´on Piura.
♣ Facultad de Ciencias.
♣ Curso Taller: Herramientas del Editor Cient´ıfico LATEX.
5.5. Listas anidadas
Pueden crearse listas de listas, hasta cuatro niveles de inclusi´on (por defecto).
Los siguientes son dos ejemplos que muestran listas de listas, con cuatro
niveles de inclusi´on:
begin{itemize}
item Primer elemento del primer nivel.
item Segundo elemento del primer nivel.
begin{itemize}
item Primer elemento del segundo nivel.
begin{itemize}
item Primer elemento del tercer nivel.
begin{itemize}
item Primer elemento del cuarto nivel.
end{itemize}
item Segundo elemento del tercer nivel.
end{itemize}
item Segundo elemento del segundo nivel.
end{itemize}
item Tercer elemento del primer nivel.
end{itemize}

78. 70 CAP´ITULO 5. LISTAS
Primer elemento del primer nivel.
Segundo elemento del primer nivel.
• Primer elemento del segundo nivel.
◦ Primer elemento del tercer nivel.
Primer elemento del cuarto nivel.
◦ Segundo elemento del tercer nivel.
• Segundo elemento del segundo nivel.
Tercer elemento del primer nivel.
begin{enumerate}
item Primer elemento del primer nivel.
item Segundo elemento del primer nivel.
begin{enumerate}
item Primer elemento del segundo nivel.
begin{enumerate}
item Primer elemento del tercer nivel.
begin{enumerate}
item Primer elemento del cuarto nivel.
end{enumerate}
item Segundo elemento del tercer nivel.
end{enumerate}
item Segundo elemento del segundo nivel.
end{enumerate}
item Tercer elemento del primer nivel.
end{enumerate}
1. Primer elemento del primer nivel.
2. Segundo elemento del primer nivel.
a) Primer elemento del segundo nivel.
1) Primer elemento del tercer nivel.
a Primer elemento del cuarto nivel.
2) Segundo elemento del tercer nivel.
b) Segundo elemento del segundo nivel.
3. Tercer elemento del primer nivel.

79. 5.5. LISTAS ANIDADAS 71
Adem´as, pueden incluirse listas dentro de otras de distinto tipo, hasta cua-
tro niveles de inclusi´on (por defecto).
El siguiente es un ejemplo que muestra listas mixtas, con cuatro niveles de
inclusi´on:
begin{itemize}
item Primer nivel en texttt{itemize} (primer nivel global)
begin{enumerate}
item Primer nivel en texttt{enumerate} (segundo nivel
global).
begin{itemize}
item Segundo nivel en texttt{itemize} (tercero global).
begin{enumerate}
item Segundo nivel en texttt{enumerate} (cuarto global).
item Segundo elemento del cuarto nivel global.
end{enumerate}
item Vuelta al tercer nivel global (segundo en
texttt{itemize}).
end{itemize}
item Segundo nivel global (primer en texttt{enumerate}).
end{enumerate}
item Primer nivel global.
end{itemize}
Primer nivel en itemize (primer nivel global)
1. Primer nivel en enumerate (segundo nivel global).
• Segundo nivel en itemize (tercero global).
a) Segundo nivel en enumerate (cuarto global).
b) Segundo elemento del cuarto nivel global.
• Vuelta al tercer nivel global (segundo en itemize).
2. Segundo nivel global (primer en enumerate).
Primer nivel global.

80. 72 CAP´ITULO 5. LISTAS
5.6. Manipulaci´on de etiquetas en el entorno
enumerate
El estilo de numeraci´on y las etiquetas que se˜nalan cada lista son configurables
f´acilmente. En el entorno enumerate, las etiquetas por defecto son:
begin{enumerate}
item Etiqueta de primer nivel
begin{enumerate}
item Etiqueta de segundo nivel
begin{enumerate}
item Etiqueta de tercer nivel
begin{enumerate}
item Etiqueta de cuarto nivel
item Etiqueta de cuarto nivel
end{enumerate}
item Etiqueta de tercer nivel
end{enumerate}
item Etiqueta de segundo nivel
end{enumerate}
item Etiqueta de primer nivel
end{enumerate}
1. Etiqueta de primer nivel
a) Etiqueta de segundo nivel
1) Etiqueta de tercer nivel
a Etiqueta de cuarto nivel
b Etiqueta de cuarto nivel
2) Etiqueta de tercer nivel
b) Etiqueta de segundo nivel
2. Etiqueta de primer nivel
La numeraci´on por defecto en la lista de nivel uno est´a formada por n´ume-
ros ar´abigos, el nivel dos por letras en min´usculas, el nivel tres son n´umeros
nuevamente y el cuatro, letras con ap´ostrofe. Cada una de estas etiquetas pue-
de cambiarse redefiniendo apropiadamente los comandos que las generan. Tales
comandos son: theenumi, theenumii, theenumiii y theenumiv, uno pa-
ra cada nivel. Mientras que las etiquetas que generan la construcci´on de dichos

81. 5.6. MANIPULACI ´ON DE ETIQUETAS EN EL ENTORNO ENUMERATE 73
comandos son labelenumi, labelenumii, labelenumiii y labelenumiv.
Si se quiere cambiar este comportamiento por defecto en cualquier nivel, es
necesario redefinir ambos comandos, justo antes del inicio del entorno corres-
pondiente. Por ejemplo:
renewcommand{theenumii}{arabic{enumii}}
renewcommand{labelenumii}{theenumi.theenumii.}
renewcommand{labelenumiii}{theenumi.theenumii.
theenumiii.}
renewcommand{theenumiv}{arabic{enumiv}}
renewcommand{labelenumiv}{theenumi.theenumii.
theenumiii.theenumiv.}
begin{enumerate}
item Etiqueta de primer nivel
begin{enumerate}
item Etiqueta de segundo nivel
begin{enumerate}
item Etiqueta de tercer nivel
begin{enumerate}
item Etiqueta de cuarto nivel
item Etiqueta de cuarto nivel
end{enumerate}
item Etiqueta de tercer nivel
end{enumerate}
item Etiqueta de segundo nivel
end{enumerate}
item Etiqueta de primer nivel
end{enumerate}
1. Etiqueta de primer nivel
1.1. Etiqueta de segundo nivel
1.1. 1. Etiqueta de tercer nivel
1.1. 1.1. Etiqueta de cuarto nivel
1.1. 1.2. Etiqueta de cuarto nivel
1.1. 2. Etiqueta de tercer nivel
1.2. Etiqueta de segundo nivel
2. Etiqueta de primer nivel
Los comandos que permiten cambiar el estilo de la numeraci´on son arabic
(n´umeros ar´abigos), roman, Roman (numeraci´on romana, en min´usculas y

82. 74 CAP´ITULO 5. LISTAS
may´usculas) y alph, Alph (numeraci´on alfab´etica, en min´usculas y may´uscu-
las). T´engase en cuenta que listas alfab´eticas con m´as elementos que letras del
alfabeto generar´a errores en la compilaci´on.
renewcommand{theenumi}{Roman{enumi}}
renewcommand{labelenumi}{[textbf{theenumi}]}
renewcommand{theenumii}{Alph{enumii}}
renewcommand{labelenumii}{[textbf{theenumi}-
textit{theenumii}]}
begin{enumerate}
item Etiqueta de primer nivel
begin{enumerate}
item Etiqueta de segundo nivel
item Etiqueta de segundo nivel
end{enumerate}
item Etiqueta de primer nivel
end{enumerate}
[I] Etiqueta de primer nivel
[I- A] Etiqueta de segundo nivel
[I- B] Etiqueta de segundo nivel
[II] Etiqueta de primer nivel
5.7. Manipulaci´on de etiquetas en el entorno
itemize
El esquema de etiquetas por defecto en este entorno es $blacksquare$ ( )
en el nivel uno, $bullet$ (•) en el nivel dos, $circ$ (◦) en el nivel tres
y $diamond$ ( ) en el nivel cuatro. La modificaci´on de estas etiquetas se
lleva a cabo redefiniendo los comandos del nivel correspodiente labelitemi,
labelitemii, labelitemiii y labelitemiv.

83. Cap´ıtulo 6
La bibliograf´ıa
6.1. El entorno thebibliography
La bibliograf´ıa es el entorno que permite al autor listar las referencias utilizadas
y citarlas en alg´un punto del texto. La estructura es similar a la de una lista
enumerada donde cada entrada viene marcada por el comando bibitem y es
referenciada desde el comando cite, que producir´a un n´umero de referencia
o el nombre del autor, seg´un sea el estilo escogido.
El entorno se define del siguiente modo:
begin{thebibliography}[etiqueta mayor]
bibitem[leyenda1]{referencia1} T´ıtulo, autor, ...
bibitem[leyenda2]{referencia2} T´ıtulo, autor, ...
end{thebibliography}
El argumento etiqueta mayor indica el n´umero de referencias que vaya
a aparecer. Por ejemplo, si vamos a introducir entre 10 y 99 publicaciones,
entonces deberemos comenzar con begin{thebibliography}[99].
El argumento opcional de bibitem, leyenda se utiliza para modificar la
identificaci´on en la lista de referencias, en lugar de un n´umero. El argumento
referencia ser´a la etiqueta usada para referenciar la cita. Se usa a trav´es del
comando cite:
cite{etiqueta1}
cite{etiqueta1,etiqueta2,...}
75

84. 76 CAP´ITULO 6. LA BIBLIOGRAF´IA
Si queremos a˜nadir alg´un dato m´as a la referencia (n´umero de p´agina donde
aparece, o el cap´ıtulo, etc.) usamos un argumento opcional:
cite[P´agina 25]{etiqueta1}
...
La referencia cl´asica en LaTeX es cite{Gr}.
Otras referencias interesantes son cite{Gu,Kn}.
...
begin{thebibliography}{9}
...
bibitem{Gr} Griffiths, D and Higham, D. LEARNING LaTeX.
The Society for Industrial and Applied Mathematics (1997).
bibitem{Gu} Gurari, E. WRITING WITH TeX. McGraw-Hill,
Inc. (1994).
bibitem{Kn} Knuth, D. THE TeX BOOK. Adisson-Wesley
Publishing Company (1991).
end{thebibliography}
La referencia cl´asica en LATEX es [3]. Otras referencias interesantes son [4, 5].
6.1.1. ´Indice de contenidos
El entorno thebibliography crea una secci´on del documento a modo de
cap´ıtulo (si la clase de documento es report o book) o secci´on (si la clase
es article). Sin embargo no aparece listado en el ´ındice de contenidos. Para
introducir dicho cap´ıtulo o secci´on en el ´ındice es necesario a˜nadir una l´ınea
como la que sigue:
addcontentsline{Extensi´on de archivo}{Unidad}{Texto de entrada}
El par´ametro Extensi´on de archivo se refiere a uno de los archivos donde
LATEXalmacena informaci´on sobre ´ındices de contenido, de figuras o tablas. Las
extensiones respectivas son toc, lof o lot.
El argumento Unidad se refiere a qu´e tipo de unidad de estructura queremos
asimilar dicha entrada, es decir, si se trata de una secci´on, un cap´ıtulo, etc.
Los valores ser´an section, chapter, etc.

85. 6.2. EL PROGRAMA BIBTEX 77
El Texto de entrada el lo que deseamos que aparezca en el ´ındice corres-
pondiente. As´ı, en un libro, la entrada a incluir ser´a:
addcontentsline{toc}{chapter}{Bibliograf´ıa}
6.2. El programa BibTEX
La elaboraci´on de entornos para bibliograf´ıa puede automatizarse c´omodamen-
te usando el programa BibTEX. Dicho programa crea un entorno bibliogr´afico
para un documento concreto a partir de una base de datos previamente cons-
truida. De este modo, s´olo es necesario mantener una base de datos y recurrir
a ella para construir la bibliograf´ıa de cada documento que escribamos.
La base de datos consiste en uno o varios archivos con extensi´on .bib que
deben poseer una estructura concreta. Por cada referencia debemos incluir una
entrada en dicho archivo, que ser´a etiquetada de forma similar a lo que se hace
en un bibitem.
En el momento en el que aparezca una cita a una de las referencias de
nuestra base de datos, ´esta ser´a autom´aticamente incluida en la bibliograf´ıa
del mismo a trav´es del programa BibTEX.
Para usar dicho programa debemos incluir en nuestro archivo fuente un co-
mando que llame a la base o bases de datos que queramos utilizar, del siguiente
modo:
bibliography{database1,database2}
El comando anterior especifica que las entradas bibliogr´aficas se colocar´an
en la posici´on en la que aparece dicho comando y ser´an extra´ıdas de los archivos
database1.bib y database2.bib.
El estilo que aparecer´a en la bibliograf´ıa viene especificado por el comando
bibliographystyle, que determinar´a el formato en el que aparecer´an las
diferentes entradas. Por ejemplo:
bibliographystyle{plain}
especifica que las entradas ser´an formateadas seg´un el estilo plain que se

86. 78 CAP´ITULO 6. LA BIBLIOGRAF´IA
encuentra descrito en el archivo (plain.bst). Es posible situar este comando
en cualquier punto del documento despu´es de begin{document}.
6.2.1. Estilos de BibTEX
plain Estilo est´andar. Las entradas son numeradas correlativamente por or-
den alfab´etico de autores.
unsrt Similar al estilo plain, pero las entradas son numeradas en el orden en
que son citadas en el documento.
alpha Se diferencia con el estilo plain, en que las etiquetas de las entradas
est´an formadas por el nombre del autor y el a˜no de publicaci´on, en lugar
de ser n´umeros.
abbrv Similar al estilo plain, pero las entradas son m´as compactas, quedando
abreviados los nombres de pila de los autores, las revistas, etc.
acm Estilo usado en las revistas de la ACM (Association for Computing Ma-
chinery).
apalike Estilo usado en las revistas de la American Psychology Association
(APA). Precisa del paquete apalike.
Adem´as varias organizaciones, revistas, etc. han desarrollado sus propios es-
tilos bibliogr´aficos, algunos de los cuales vienen con la distribuci´on MiKTEX(v´ease
C:Archivos de programaMiKTeX 2.9bibtexbst).
6.2.2. Pasos para ejecutar BibTEX con LATEX
1. Al correr LATEX, se generar´a un listado de referencias para cada comando
cite que est´e presente. Dicho listado aparecer´a en el archivo auxiliar
.aux.
2. Ejecutar BibTEX, el cual leer´a dicho archivo, las bases de datos y el
archivo de estilo y escribir´a un archivo .bbl que contiene un entorno
bibliograf´ıa formateado seg´un el archivo .bst escogido. Los errores o
avisos ser´an escritos en un archivo .blg.
3. En la siguiente compilaci´on de LATEX, se lee el archivo .bbl.
4. Una tercera compilaci´on resuelve todas las referencias cruzadas.

87. 6.2. EL PROGRAMA BIBTEX 79
N´otese que las referencias que aparecer´an en el texto son aquellas que hayan
sido citadas mediante cite, y no todas las presentes en la base de datos .bib.
En ocasiones, es posible querer incluir publicaciones que no son expl´ıcita-
mente citadas. Pare ellos usamos el comando n cualquier parte del documento.
Dicho comando no produce texto alguno pero hace que la referencia citada sea
incluida por BibTEX. El comando nocite{*} hace que todas las entradas de
la base de datos sean incluidas.
6.2.3. Creaci´on de bases de datos bibliogr´aficos
La ventaja principal del uso del programa BibTEX es la no necesidad de escribir
un listado de referencias para cada documento. Las referencias son escritas una
sola vez y almacenadas en la(s) base(s) de datos correspondiente(s) para usos
futuros.
No obstante, es necesario crear las entradas de la base de datos seg´un un
formato espec´ıfico. Lo que sigue es un ejemplo de entrada:
@BOOK{knuth:86a,
AUTHOR ="Donald E. Knuth",
TITLE ={The TeXbook},
EDITION ="third"
PUBLISHER ="Addison-Wesley",
ADDRESS ={Reading, MA},
YEAR =1986}
La primera palabra, prefijada por @, determina el tipo de entrada, que va-
riar´a seg´un el tipo de publicaci´on que sea: libros, art´ıculos, prepublicaciones,
etc. El resto de la informaci´on es escrita entre llaves, comenzando por la etique-
ta (la que usaremos para la referencia con el comando cite), En el ejemplo
anterior pondr´ıamos cite{knuth:86a}. El resto de la informaci´on sobre la
referencia es introducida mediante varios campos, separados por comas, en el
formato que se aprecia. Los espacios son opcionales. La informaci´on de cada
campo puede ser incluida entre llaves o entre comillas dobles; sin embargo, si
la informaci´on del campo consta ´unicamente de n´umeros, no son necesarios
los delimitadores. Cada tipo de entrada tiene una serie de campos requeridos
y otros opcionales. En caso de ausencia de alg´un campo requerido BibTEX
dar´a un informe de error.

88. 80 CAP´ITULO 6. LA BIBLIOGRAF´IA
Los tipos de referencias, los campos requeridos y los opcionales son:
@article Art´ıculos en revistas.
campos requeridos author, title, journal, year.
campos opcionales volume, number, pages, month, note.
@book Libros con editorial conocida.
campos requeridos author or editor, title, publisher, year.
campos opcionales volume or number, series, address, edition, month,note.
@booklet Libros sin conocimiento de la editorial que lo publica.
campos requeridos title.
campos opcionales author, howpublished, address, month, year, note.
@conference Art´ıculo en un recopilatorio de una conferencia.
campos requeridos author, title, booktitle, year.
campos opcionales editor, volume or number, series, pages, address, month,
organization, publisher, note.
@inbook Entrada para una parte de un libro.
campos requeridos author or editor, title, chapter and/or pages, publis-
her, year.
campos opcionales volume or number, series, type, address, edition, month,
note.
@incollection Entrada para una parte de un libro con t´ıtulo propio.
campos requeridos author, title, booktitle, publisher, year.
campos opcionales editor, volume or number, series, type, chapter, pa-
ges, address, edition, month, note.
@inproceedings Art´ıculo en las publicaciones de un congreso.
campos requeridos author, title, booktitle, year.
campos opcionales editor, volume or number, series, pages, address, month,
organization, publisher, note.
@manual Entrada para documentaci´on de tipo t´ecnico.
campos requeridos title.

89. 6.2. EL PROGRAMA BIBTEX 81
campos opcionales author, organisation, address, edition, month, year,
note.
@masterthesis Entrada para proyecto, tesina o master.
campos requeridos author, title, school, year.
campos opcionales type, address, month, note.
@misc Documento que no se ajusta a ninguno de los dem´as tipos.
campos requeridos none.
campos opcionales author, title, howpublished, month, year, note.
@phdthesis Tesis doctoral.
campos requeridos author, title, school, year.
campos opcionales type, address, month, note.
@proceedings campos requeridos title, year.
campos opcionales editor, volume or number, series, address, month, or-
ganization, publisher, note.
@unpublished Documento no publicado con t´ıtulo y autor.
campos requeridos author, title, note.
campos opcionales month, year.

90. Cap´ıtulo 7
Documentos b´asicos
7.1. Art´ıculo
documentclass[opciones]{article}
Pre´ambulo
declaraciones: paquetes, comandos
t´ıtulo, autor, fecha
begin{document}
Documento



maketitle
begin{abstract}...end{abstract}
tableofcontents
section{...}
subsection{...}
subsubsection{...}
begin{thebibliography}
. . .
end{thebibliography}
end{document}
Para elaborar un art´ıculo con TEXMAKER realizamos los siguientes pasos:
1. Clic en la opci´on Asitentes de la barra de men´u.
2. Clic en la opci´on Asistente para nuevo documento.
3. Completar el cuadro desplegado de manera similar a la indicada en la
figura 7.1 y hacer clic en el bot´on aceptar.
4. Editar el c´odigo impreso (Fig. 7.2) de acuerdo a nuestro requerimiento.
82

91. 7.1. ART´ICULO 83
Figura 7.1: Asistente para nuevo art´ıculo de TEXMAKER
Figura 7.2: C´odigo obtenido con el asistente de TEXMAKER.

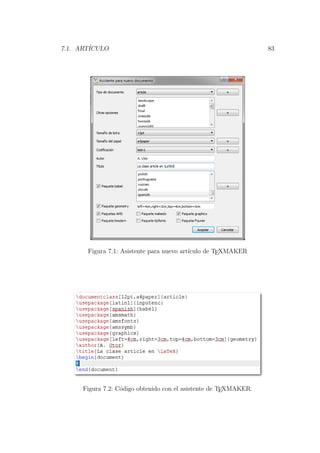
92. 84 CAP´ITULO 7. DOCUMENTOS B ´ASICOS
El documento obtenido con el siguiente c´odigo se aprecia en la figura 7.3.
documentclass[a4paper]{article}
usepackage[latin1]{inputenc}
usepackage[spanish]{babel}
usepackage{amsmath}
usepackage{amsfonts}
usepackage{amssymb}
usepackage{graphicx}
usepackage[left=4cm,right=3cm,top=4cm,bottom=3cm]{geometry}
author{A. Utor thanks{Catedr´atico, UNP, autor@unp.edu.pe}}
title{La clase article en LaTeX}
date{}
begin{document}
maketitle
tableofcontents
begin{abstract}
En este documento se exhibir´an las caracter´ısticas m´as
importantes de un art´ıculo escrito en LaTeX.
end{abstract}
section{Art´ıculo en LaTeX}
Los art´ıculos son la clase de documentos LaTeX m´as ampliamente
utilizados, dada la sencillez en su creaci´on.
subsection{Estructura de un art´ıculo}
Este tipo de documento se puede dividir en dos partes, los campos
de identificaci´on: t´ıtulo, autor y fecha. Y el cuerpo del
documento, en el cual el texto pertenece a una de las siguientes
unidades divisionales: resumen, secciones, subsecciones,
par´agrafos, subpar´agrafos, etc.
begin{thebibliography}{9}
bibitem{Ar} Aranda, E. CURSO DE LaTeX. Departamento de
Matem´aticas, E.T.S. Ingenieros Industriales, Universidad de
Castilla, La Mancha. (2008).
end{thebibliography}
end{document}

93. 7.1. ART´ICULO 85
La clase article en LATEX
A. Utor *
´Indice
1. Art´ıculo en LATEX 1
1.1. Estructura de un art´ıculo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
Resumen
En este documento se exhibir´an las caracter´ısticas m´as importantes de un art´ıculo
escrito en LATEX.
1. Art´ıculo en LATEX
Los art´ıculos son la clase de documentos LATEX m´as ampliamente utilizados, dada la
sencillez en su creaci´on.
1.1. Estructura de un art´ıculo
Este tipo de documento se puede dividir en dos partes, los campos de identificaci´on:
t´ıtulo, autor y fecha. Y el cuerpo del documento, en el cual el texto pertenece a una de las
siguientes unidades divisionales: resumen, secciones, subsecciones, par´agrafos, subpar´agrafos,
etc.
Referencias
[1] Aranda, E. CURSO DE LATEX. Departamento de Matem´aticas, E.T.S. Ingenieros Indus-
triales, Universidad de Castilla, La Mancha. (2008).
*Catedr´atico, UNP, autor@unp.edu.pe
1
Figura 7.3: Art´ıculo.

94. 86 CAP´ITULO 7. DOCUMENTOS B ´ASICOS
7.2. Libro
documentclass[opciones]{book}
Pre´ambulo
declaraciones: paquetes, comandos
t´ıtulo, autor, fecha
begin{document}
Documento



maketitle
frontmatter
tableofcontents
mainmatter
chapter{...}
section{...}
subsection{...}
subsubsection{...}
appendix
backmatter
begin{thebibliography}
. . .
end{thebibliography}
end{document}
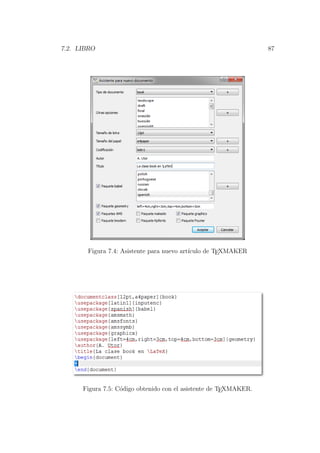
Para elaborar un libro con TEXMAKER realizamos los siguientes pasos:
1. Clic en la opci´on Asitentes de la barra de men´u.
2. Clic en la opci´on Asistente para nuevo documento.
3. Completar el cuadro desplegado de manera similar a la indicada en la
figura 7.4 y hacer clic en el bot´on aceptar.
4. Editar el c´odigo impreso (Fig. 7.5) de acuerdo a nuestro requerimiento.
El documento obtenido con el siguiente c´odigo se aprecia en las figuras 7.6,
7.7, 7.8, 7.9 y 7.10.
documentclass[a4paper]{book}
usepackage[latin1]{inputenc}
usepackage[spanish]{babel}
usepackage{amsmath}

95. 7.2. LIBRO 87
Figura 7.4: Asistente para nuevo art´ıculo de TEXMAKER
Figura 7.5: C´odigo obtenido con el asistente de TEXMAKER.

96. 88 CAP´ITULO 7. DOCUMENTOS B ´ASICOS
usepackage{amsfonts}
usepackage{amssymb}
usepackage{graphicx}
usepackage[left=4cm,right=3cm,top=4cm,bottom=3cm]{geometry}
author{A. Utor thanks{Catedr´atico, UNP, autor@unp.edu.pe}}
title{La clase book en LaTeX}
date{}
begin{document}
maketitle
frontmatter
chapter{Pr´ologo}
La clase book facilita la digitaci´on de libros de alta calidad.
tableofcontents
mainmatter
chapter{Libro en LaTeX}
Los libros son la clase de documentos LaTeX m´as completa.
section{Estructura de un libro}
Este tipo de documento se puede dividir en tres partes, la
apertura: pr´ologo, agradecimientos, tabla de contenidos, etc.
La parte central del documento, en la que se desarrolla el
tema tratado y el texto pertenece a una de las siguientes
unidades divisionales: cap´ıtulos secciones, subsecciones, etc.
Y el cierre del documento que contiene la bibliograf´ıa,
conclusiones, recomendaciones, etc.
backmatter
begin{thebibliography}{9}
bibitem{Ar} Aranda, E. CURSO DE LaTeX. Departamento de
Matem´aticas, E.T.S. Ingenieros Industriales, Universidad de
Castilla, La Mancha. (2008).
end{thebibliography}
end{document}

97. 7.2. LIBRO 89
La clase book en LATEX
A. Utor 1
1
Catedr´atico, UNP, autor@unp.edu.pe
Figura 7.6: Portada del libro.

98. 90 CAP´ITULO 7. DOCUMENTOS B ´ASICOS
Pr´ologo
La clase book facilita la digitaci´on de libros de alta calidad.
i
Figura 7.7: ´Indice general del libro.

99. 7.2. LIBRO 91
´Indice general
Pr´ologo I
1. Libro en LATEX 1
1.1. Estructura de un libro . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
iii
Figura 7.8: Pr´ologo del libro.

100. 92 CAP´ITULO 7. DOCUMENTOS B ´ASICOS
Cap´ıtulo 1
Libro en LATEX
Los libros son la clase de documentos LATEX m´as completa.
1.1. Estructura de un libro
Este tipo de documento se puede dividir en tres partes, la apertura: pr´ologo, agradeci-
mientos, tabla de contenidos, etc. La parte central del documento, en la que se desarrolla el
tema tratado y el texto pertenece a una de las siguientes unidades divisionales: cap´ıtulos sec-
ciones, subsecciones, etc. Y el cierre del documento que contiene la bibliograf´ıa, conclusiones,
recomendaciones, etc.
1
Figura 7.9: Cap´ıtulo 1 del libro.

101. 7.2. LIBRO 93
Bibliograf´ıa
[1] Aranda, E. CURSO DE LATEX. Departamento de Matem´aticas, E.T.S. Ingenieros Indus-
triales, Universidad de Castilla, La Mancha. (2008).
3
Figura 7.10: Bibliograf´ıa del libro.

102. 94 CAP´ITULO 7. DOCUMENTOS B ´ASICOS
7.3. Diapositivas
documentclass[opciones]{beamer}
Pre´ambulo
declaraciones: temas, paquetes, comandos
autor, t´ıtulo, logo, instituto, fecha
begin{document}
Documento



maketitle
begin{frame}titlepageend{frame}
begin{frame}tableofcontentsend{frame}
begin{frame}{<T´ıtulo>}
...
end{frame}
. . .
begin{frame}{<T´ıtulo>}
...
end{frame}
begin{frame}
begin{thebibliography}
. . .
end{thebibliography}
end{frame}
end{document}
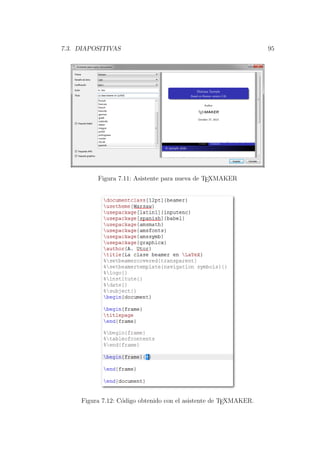
Para elaborar diapositivas con TEXMAKER realizamos los siguientes pasos:
1. Clic en la opci´on Asitentes de la barra de men´u.
2. Clic en la opci´on Quick beamer presentation.
3. Completar el cuadro desplegado de manera similar a la indicada en la
figura 7.11 y hacer clic en el bot´on aceptar.
4. Editar el c´odigo impreso (Fig. 7.12) de acuerdo a nuestro requerimiento.

103. 7.3. DIAPOSITIVAS 95
Figura 7.11: Asistente para nueva de TEXMAKER
Figura 7.12: C´odigo obtenido con el asistente de TEXMAKER.

104. 96 CAP´ITULO 7. DOCUMENTOS B ´ASICOS
El documento obtenido con el siguiente c´odigo se aprecia en las figuras 7.13,
7.14 y 7.15.
documentclass[12pt]{beamer}
usetheme{Warsaw}
usepackage[latin1]{inputenc}
usepackage[spanish]{babel}
deftranslation[to=spanish]{Theorem}{Teorema}
usepackage{amsmath}
usepackage{amsfonts}
usepackage{amssymb}
usepackage{graphicx}
usepackage{multicol}
author{A. Utor thanks{Catedr´atico, UNP, autor@unp.edu.pe}}
title{La clase beamer en LaTeX}
%setbeamercovered{transparent}
%setbeamertemplate{navigation symbols}{}
%logo{}
%institute{}
%date{}
%subject{}
begin{document}
begin{frame}
titlepage
end{frame}
begin{frame}
tableofcontents
end{frame}
section{Primera secci´on}
begin{frame}{Primera diapositiva}
Una f´ormula:
[int_{-infty}^infty e^{-x^2} , dx = sqrt{pi}]
Una lista:
begin{multicols}{2}
begin{itemize}
item itemized item 1
item itemized item 2
item itemized item 3

105. 7.3. DIAPOSITIVAS 97
end{itemize}
begin{enumerate}
item enumerated item 1
item enumerated item 2
item enumerated item 3
end{enumerate}
end{multicols}
begin{theorem}
En un tri´angulo rect´angulo, el cuadrado de la hipotenusa
es igual a la suma de los cuadrados de los otros dos lados.
end{theorem}
end{frame}
section{Bibliograf´ıa}
begin{frame}
begin{thebibliography}{9}
bibitem{Ar} Aranda, E. CURSO DE LaTeX. Departamento de
Matem´aticas, E.T.S. Ingenieros Industriales, Universidad de
Castilla, La Mancha. (2008).
end{thebibliography}
end{frame}
end{document}
Primera secci´on
Bibliograf´ıa
La clase beamer en LATEX
A. Utor 1
31 de enero de 2014
1
Catedr´atico, UNP, autor@unp.edu.pe
A. Utor La clase beamer en LATEX
Figura 7.13: Portada de las diapositivas.

106. 98 CAP´ITULO 7. DOCUMENTOS B ´ASICOS
Primera secci´on
Bibliograf´ıa
1 Primera secci´on
2 Bibliograf´ıa
A. Utor La clase beamer en LATEX
Figura 7.14: ´Indice general de las diapositivas.
Primera secci´on
Bibliograf´ıa
Primera diapositiva
Una f´ormula: ∞
−∞
e−x2
dx =
√
π
Una lista:
itemized item 1
itemized item 2
itemized item 3
1 enumerated item 1
2 enumerated item 2
3 enumerated item 3
Teorema
En un tri´angulo rect´angulo, el cuadrado de la hipotenusa es
igual a la suma de los cuadrados de los otros dos lados.
A. Utor La clase beamer en LATEX
Figura 7.15: Contenido de las diapositivas.

107. 7.3. DIAPOSITIVAS 99
Primera secci´on
Bibliograf´ıa
Aranda, E. CURSO DE LATEX. Departamento de
Matem´aticas, E.T.S. Ingenieros Industriales, Universidad
de Castilla, La Mancha. (2008).
A. Utor La clase beamer en LATEX
Figura 7.16: Bibliograf´ıa de las diapositivas.

108. Cap´ıtulo 8
Elementos de programaci´on
8.1. Creaci´on de comandos y entornos
8.1.1. Comandos
En ´esta secci´on describiremos c´omo utilizar el comando newcommand para
definir nuevos comandos LATEX que puedan ayudarnos a simplificar el realizar
tareas repetitivas. Para la definici´on de un nuevo comando se dispone de tres
posibilidades
newcommand{NombreComando}[NumArg][ArgDefecto]{Definici´on}
renewcommand{NombreComando}[NumArg][ArgDefecto]{Definici´on}
providecommand{NombreComando}[NumArg][ArgDefecto]{Definici´on}
donde NombreComando es el nombre que queremos asignar al nuevo comando,
NumArg indica el n´umero de argumentos que va a tener (comprendido entre 1
y 9), ArgDefecto es el valor por defecto de un argumento optativo (el primero
de ellos), y Definici´on contiene la definici´on del comando, donde los distintos
argumentos se denotan como #1, #2, etc.
Entre estas tres versiones existen diferencias importantes. newcommand se
utiliza para definir nuevos comandos, por lo que debemos estar seguros de que
el comando a definir no existe. renewcommand se utiliza para redefinir coman-
dos ya existentes, reescribiendo y borrado la definici´on anterior del comando.
Finalmente, providecommand define el nuevo comando s´olo en el caso de que
el comando no exista; en caso contrario la nueva definici´on carece de efecto.
100

109. 8.1. CREACI ´ON DE COMANDOS Y ENTORNOS 101
Para cada una de estas tres posibilidades existen versiones con y sin aste-
risco; las versiones con asterisco (newcommand*{NombreComando}[NumArg]
{ArgDef }{Def }, etc.) no permiten que los argumentos puedan extenderse a
m´as de un p´arrafo, mientras que las versiones sin asterisco (newcommand{
NombreComando}[NumArg]{ArgDef }{Def }, etc.) permiten que los argumen-
tos se extiendan a m´as de un p´arrafo.
Es preferible que ubicar las definiciones de los nuevos comandos en el
pre´ambulo.
Supongamos que la expresi´on (x1, x2, . . . , xn) aparece frecuentemente en
nuestro documento. Podemos entonces definir
newcommand{vect}{(x_1,x_2,dots,x_n)}
con lo cual, cada vez que escribamos vect (el nombre del nuevo coman-
do) se imprimir´a (x1, x2, . . . , xn).
Ahora compliquemos un poco el ejemplo con la introducci´on de argu-
mentos variables. Si por ejemplo escribimos
newcommand{vect}[1]{(#1_1,#1_2,dots,#1_n)}
(a˜nadiendo un argumento, que se sustituye en la f´ormula con “#1”),
escribiendo $vect{x}$ obtendr´ıamos (x1, x2, . . . , xn), mientras que con
$vect{a}$ se tendr´ıa (a1, a2, . . . , an), etc.
A˜nadiendo m´as argumentos, podemos obtener construcciones m´as com-
plejas, por ejemplo, definiendo
newcommand{vect}[2]{(#1_1,#1_2,dots,#1_#2)}
$vect{x}{n}$ dar´ıa como resultado (x1, x2, . . . , xn), mientras que con
$vect{a}{p}$ se obtendr´ıa (a1, a2, . . . , ap).
Practiquemos ahora la definici´on de comandos con argumentos optativos,
que toman un determinado valor por defecto. Por ejemplo, construyamos
newcommand{nuevovector}[2][x]{(#1_1,#1_2,dots,#1_#2)}
donde la “x” entre corchetes es el valor por defecto del argumento opcio-
nal (siempre el primero). As´ı, escribiendo $nuevovector{n}$ ´o
$nuevovector{p}$ obtendr´ıamos (x1, x2, . . . , xn) y (x1, x2, . . . , xp) res-
pectivamente, mientras que a˜nadiendo un argumento optativo cambia
r´ıamos el valor por defecto de “x”, $nuevovector[a]{n}$ dar´ıa
(a1, a2, . . . , an).

110. 102 CAP´ITULO 8. ELEMENTOS DE PROGRAMACI ´ON
8.1.2. Entornos
Tambi´en es posible definir nuevos entornos, o redefinir entornos ya existentes;
para ello se dispone de los siguientes comandos
newenvironment{NombreEntorno}[NumArg][ArgDef ]
{DefEntrada}{DefSalida}
renewenvironment{NombreEntorno}[NumArg][ArgDef ]
{DefEntrada}{DefSalida}
que funcionan de un modo similar a los comandos del tipo newcommand, en
cuanto a que admiten argumentos (hasta 9), opcionalmente con el primero
de ellos optativo. La diferencia reside en que en el argumento DefEntrada se
indican las ´ordenes que se deben ejecutar antes de entrar en el entorno, y en
el argumento DefSalida la que se deben ejecutar al salir del entorno. Una vez
definido el nuevo entorno, se debe invocar de la siguiente forma
begin{NuevoEntorno}{Arg1}...{ArgN }
Cuerpo del entorno
end{NuevoEntorno}
Al igual que en el caso de los comandos, existen versiones sin y con as-
terisco, con el mismo significado, es decir, que respectivamente admiten o no
argumentos de m´as de un p´arrafo.
Por ejemplo, construyamos un entorno que cree una minip´agina de anchura
variable por defecto media p´agina), centrada, y con el texto en negrita
newenvironment{mientorno}[1][0.5]%
{begin{center}begin{minipage}{#1textwidth}bfseries}%
{end{minipage}end{center}}
y tras definir ´este nuevo entorno, digitando
begin{mientorno}
Ejemplo de texto con una anchura est´andar de media
p´agina, centrado, y en tipo de letra negrita.
end{mientorno}

111. 8.1. CREACI ´ON DE COMANDOS Y ENTORNOS 103
obtenemos
Ejemplo de texto con una anchura
est´andar de media p´agina, centra-
do, y en tipo de letra negrita.
o, si queremos emplear el argumento optativo y reducir la anchura del texto a
0, 3 veces la anchura de texto (textwidth)
begin{mientorno}[0.3]
Ejemplo de texto con una anchura de un tercio de p´agina,
centrado, y en tipo de letra negrita
end{mientorno}
Ejemplo de texto
con una anchura de
un tercio de p´agina,
centrado, y en tipo
de letra negrita
Es importante tener en cuenta que los argumentos de un entorno s´olo pue-
den utilizarse en la definici´on de entrada (DefEntrada). Si los necesitamos en
la definici´on de salida, podemos utilizar el “truco” de guardarlos conveniente-
mente, empleando un comando newcommand para ello. En el siguiente ejemplo,
creamos un entorno cita para escribir citas, dando el nombre del autor como
argumento
newenvironment{cita}[1]{newcommand{autor}{#1}%
begin{quote}itshape‘‘}{’’end{quote}centerline{autor}}
Tras lo cual, por ejemplo,
begin{cita}{Andres Fern´andez}
Nuestras vidas son los r´ıos que van a parar al mar,
que es el morir
end{cita}
produce
“ Nuestras vidas son los r´ıos que van a parar al mar, que es el
morir. ”
Andres Fern´andez

112. 104 CAP´ITULO 8. ELEMENTOS DE PROGRAMACI ´ON
8.2. Contadores y longitudes
8.2.1. Contadores
En su funcionamiento habitual, LATEX utiliza un amplio n´umero de contadores
con el fin de enumerar distintos elementos de un documento: p´aginas, secciones,
tablas, figuras, etc. Cada contador tiene un nombre que permite identificarlo;
as´ı, page es el contador que identifica p´aginas, chapter, cap´ıtulos, etc. En
lo sucesivo, denotaremos ese nombre como NombreContador. Cada contador
lleva asociados una serie de elementos de diferente significado: nombre, valor
(siempre un n´umero entero) y formato, ´este ´ultimo pudiendo tomar variadas
formas: (I, II, III..., a, b, c...)
Se dispone de los siguientes formatos de contador
arabic{NombreContador} 1, 2, 3, ...
alph{NombreContador} a, b, c, ... (vea nota 1)
Alph{NombreContador} A, B, C, ... (vea nota 1)
roman{NombreContador} I, II, III, ... (vea nota 2)
Roman{NombreContador} I, II, III, ...
fnsymbol{NombreContador} *, **, ***, ... (vea nota 3)
Nota 1. El valor del contador no puede superar 27 (n´umero de letras en el
abecedario.
Nota 2. El resultado mostrado es el que se obtiene con babel, opci´on spanish.
Sin ello, se obtendr´ıa i, ii, iii, ... No obstante, aunque se use el paque-
te babel con la opci´on spanish es posible obtener las min´usculas en la
numeraci´on romana insertando el siguiente c´odigo en el pre´ambulo:
makeatletter
def@roman#1{romannumeral #1}
makeatother
Nota3. Igualmente, el resultado mostrado es el obtenido con babel y spanish;
en caso contrario, se utilizan las marcas inglesas: ∗, †, ‡, .... En ambos
casos, el valor no puede ser superior a 6.
Asociado a cada contador existe un comando, llamado representaci´on del
contador, que permite imprimir el valor del contador NombreContador en al-
guno de los formatos descritos; el comando es theNombreContador.

113. 8.2. CONTADORES Y LONGITUDES 105
Cuando LATEX define un nuevo contador, le asigna inicialmente la represen-
taci´on correspondiente al formato arabic; si queremos cambiarla, podemos
redefinirla mediante el comando renewcommand*; veamos unos ejemplos de lo
que se puede hacer
Este ejemplo muestra c´omo obtener
el n´umero de la p´agina en curso; ´esta
p´agina es la n´umero thepage, en la
representaci´on original.
renewcommand*{thepage}{roman{page}}
Ahora esta cambiada a n´umeros romanos; ´esta
p´agina es la n´umero thepage.
renewcommand*{thepage}{[Sec.
thesection -- P´ag. arabic{page}]}
Luego, algo m´as elaborado; ´esta p´agina
es la n´umero thepage.
renewcommand*{thepage}{arabic{page}}
Finalmente, volvemos al formato original; ´esta
p´agina es la n´umero thepage.
Este ejemplo muestra c´omo obtener el n´umero de la p´agina en
curso; ´esta p´agina es la n´umero 105, en la representaci´on original.
Ahora esta cambiada a n´umeros romanos; ´esta p´agina es la n´umero
cv.
Luego, algo m´as elaborado; ´esta p´agina es la n´umero [Sec. 8.2 –
P´ag. 105].
Finalmente, volvemos al formato original; ´esta p´agina es la n´umero
105.
Es posible cambiar los valores de un contador con los siguientes comandos:
setcounter{NombreContador}{Valor} Asigna al contador NombreCon-
tador el valor entero Valor, con independencia del valor anterior.
addtocounter{NombreContador}{Valor} Incrementa NombreContador
con la cantidad Valor, que puede ser positiva o negativa.
Esta es la secci´on thesection. Pero podemos
a~nadirle 2 f´acilmente;
addtocounter{section}{2}
ahora estamos en la secci´on thesection.

114. 106 CAP´ITULO 8. ELEMENTOS DE PROGRAMACI ´ON
Mejor lo dejamos como estaba, porque si no las
restantes secciones quedar´ıan numeradas
incorrectamente (esto es, el efecto de estos
cambios de numeraci´on es emph{global}).
addtocounter{section}{-2}
Esta es la secci´on 8.2. Pero podemos a˜nadirle 2 f´acilmente; aho-
ra estamos en la secci´on 8.4. Mejor lo dejamos como estaba, porque
si no las restantes secciones quedar´ıan numeradas incorrectamente
(esto es, el efecto de estos cambios de numeraci´on es global).
Es posible recuperar el valor num´erico de un contador, independientemente
de su representaci´on, con el comando
value{NombreContador}
lo cual es ´util para la gesti´on de contadores, como veremos a continuaci´on.
Se definen nuevos contadores con la instrucci´on
newcounter{NuevoContador}[ContadorExistente]
que introduce un contador de nombre NuevoContador, y le asigna cero como
valor inicial. El argumento ContadorExistente es optativo, y sirve para subor-
dinar NuevoContador al contador ya existente ContadorExistente, de la misma
forma que, por ejemplo, el contador subsection est´a subordinado al conta-
dor section: incrementar en una unidad el contador section implica que el
contador subsection se reinicia a cero autom´aticamente.
Veamos un ejemplo de c´omo introducir un nuevo contador, con el fin de en-
lazar varias listas enumerate manteniendo la numeraci´on (enumi es el contador
est´andar LATEX para los ´ıtems de primer nivel en entornos enumerate)
Las primeras lecciones son las siguientes:
newcounter{conserva}
begin{enumerate}
item N´umeros reales
item N´umeros complejos
setcounter{conserva}{value{enumi}}

115. 8.2. CONTADORES Y LONGITUDES 107
end{enumerate}
Mas adelante, se estudiar´an temas m´as complicados:
begin{enumerate}
setcounter{enumi}{value{conserva}}
item Continuidad
item Derivaci´on
end{enumerate}
Las primeras lecciones son las siguientes:
1. N´umeros reales
2. N´umeros complejos
Mas adelante, se estudiar´an temas m´as complicados:
3. Continuidad
4. Derivaci´on
Debe mencionarse que al crear un nuevo contador se crea autom´aticamente
el comando theNuevoContador, con la definici´on arabic{NuevoContador}
por defecto.
Cuando se modifica un contador con los comandos setcounter y addtocounter,
los contadores subordinados no se ponen a cero; para obtener ´ese efecto, se dis-
pone de los comandos:
stepcounter{NombreContador} Incrementa NombreContador en una
unidad, y reinicia todos los contadores subordinados a ´este.
refstepcounter{NombreContador} Lo mismo que el anterior, pero de-
clarando tambi´en como valor del comando ref el texto generado por
theNuevoContador cuando se utilizan referencias cruzadas con los co-
mandos label y ref.
Veamos un peque˜no ejemplo que ilustra como utilizar estos comandos; de-
finimos:
newcounter{prg}[section]newcounter{linea}[prg]
newcommand*{lin}{%
addtocounter{linea}{1}thelineaquad}
renewcommand*{theprg}{arabic{section}.arabic{prg}}
newenvironment*{programa}{%

116. 108 CAP´ITULO 8. ELEMENTOS DE PROGRAMACI ´ON
refstepcounter{prg}
begin{center}Programa~theprgend{center}
obeylinesobeyspaces}{par}
Y, luego utilizamos nuestro nuevo entorno, programa, as´ı:
begin{programa}
Entrada: $N$, $x_1,x_2,ldots,x_N$.
Salida: $SUMA=sum_{i=1}^Nx_i$.
lin $SUMA=0$.
lin Para $i=1,2,ldots,N$: $SUMA=SUMA+x_i$.
lin SALIDA($SUMA$); PARAR.
end{programa}
con lo que se obtiene:
Programa 2.1
Entrada: N, x1, x2, . . . , xN .
Salida: SUMA = N
i=1 xi.
1 SUMA = 0.
2 Para i = 1, 2, . . . , N: SUMA = SUMA + xi.
3 SALIDA(SUMA); PARAR.
8.3. Longitudes
Al igual que con los contadores, LATEX es tambi´en capaz de crear y modificar
variables de tipo Longitud. Las longitudes que habitualmente utiliza LATEX
pueden tomar dos tipos de valores:
R´ıgidas: Toman un valor determinado; por ejemplo quad = 11.747 pt,
thinspace = 1.958 pt, hoffset = -28.45274 pt.
El´asticas: Toman un valor que LATEX puede modificar dentro de unos l´ımites,
a fin de optimizar la composici´on del documento. Por ejemplo, bigskip,
medskip y smallskip.

117. 8.3. LONGITUDES 109
El comando bigskip se define como:
vspace{12pt plus 4pt minus 4pt}
lo cual quiere decir que LATEX debe introducir un espacio vertical de 12 pt,
aunque tiene la libertad de incrementarlo o reducirlo en 4 pt, seg´un convenga
a fin de distribuir el espacio de forma homog´enea. Alguna de las holguras plus
o minus pueden estar ausentes en la definici´on, pero si ambas aparecen deben
estar en ´ese orden.
Los comandos bigskip, medskip y smallskip, respectivamente, tienen
asociadas longitudes el´asticas con valores almacenados en bigskipamount,
medskipamount y smallskipamount, por lo que tales comandos se definir´ıan
de hecho como:
bigskip −→ vspace{bigskipamount}
medskip −→ vspace{medskipamount}
smallskip −→ vspace{smallskipamount}
y donde cada una de ´estas longitudes el´asticas toma valores:
bigskipamount :: 12.0pt plus 4.0pt minus 4.0pt
medskipamount :: 6.0pt plus 2.0pt minus 2.0pt
smallskipamount :: 3.0pt plus 1.0pt minus 1.0pt
Puede obtenerse el valor de cualquier longitud con el comando:
theNombreLongitud
donde NombreLongitud es el nombre de la longitud; ´este comando siempre
expresa las longitudes en unidades pt, con el punto como separador decimal.
Al igual que ocurr´ıa con los contadores, los valores de una longitud pueden
modificarse. Existen dos comandos para ello:
setlength{NombreLongitud}{Valor} Asigna a la longitud
NombreLongitud un valor igual al argumento Valor, que debe ser una

118. 110 CAP´ITULO 8. ELEMENTOS DE PROGRAMACI ´ON
longitud (´esto es, expresada en unidades cm, pt, etc...). Puede ser un va-
lor tanto r´ıgido como el´astico (por ejemplo, 5mm plus 1mm minus 2mm).
Tambi´en es posible que Valor sea una variable de longitud (textwidth)
con quiz´as un factor multiplicativo (0.5textwidth, por ejemplo). Una
forma alternativa de asignar a NombreLongitud un valor es utilizar la
sintaxis:
NombreLongitud=Valor o bien NombreLongitud Valor.
addtolength{NombreLongitud}{Valor} Suma a la longitud
NombreLongitud la cantidad Valor, que puede ser positiva o negativa.
Al contrario de lo que ocurr´ıa con los contadores, cuyas asignaciones tie-
nen car´acter global (es decir, trascienden el grupo dentro del cual han sido
declaradas, y tienen efecto en todo el resto del documento), las asignaciones
de longitud tienen por defecto car´acter local ; si se realizan dentro de un grupo,
el valor anterior a la asignaci´on se recupera a la salida del grupo. En el caso de
que deseemos un efecto global, puede ser aconsejable realizar tales asignaciones
en el pre´ambulo del documento.
Se pueden definir nuevas longitudes con el comando:
newlength{NuevaLongitud}
que crea una nueva longitud llamada NuevaLongitud; es importante que
NuevaLongitud no sea ni un comando ni una longitud LATEX ya existentes, en
cuyo caso obtendr´ıamos un mensaje de error. Por defecto, las nuevas longitudes
son creadas con un valor inicial 0.0 pt.
Para la gesti´on de valores de longitud son ´utiles los siguientes comandos:
settowidth{NombreLongitud}{Objeto}
settoheight{NombreLongitud}{Objeto}
settodepth{NombreLongitud}{Objeto}
que calculan, respectivamente, la anchura (width), altura (height) y profundi-
dad1
(depth) de un objeto, asignando el valor resultante a la longitud
NombreLongitud.
1
Distancia por debajo de la l´ınea de base.

119. 8.3. LONGITUDES 111
Imaginemos que queremos medir la longitud asociada al comando quad.
Para ello podemos definir una nueva longitud:
newlength{longi}
a continuaci´on, asociamos a longi la anchura del espacio asociado al comando
quad:
settowidth{longi}{quad}
tras lo cual, el comando thelongi muestra el valor 9.99756pt.
Ahora creamos otra longitud:
newlength{longitud}
que empleamos para medir la anchura, altura, y profundidad de la palabra
Integral.
newlength{longitud}
noindent La anchura de la palabra {Large Integral}
es settowidth{longitud}{Large Integral} thelongitud,
su altura es settoheight{longitud}{Large Integral}
thelongitud y su profundidad es
settodepth{longitud}{Large Integral} thelongitud.
La anchura de la palabra Integral es 53.4619pt, su altura es 12.0pt y su
profundidad es 3.3611pt.
Veamos un ´ultimo ejemplo:
newlength{longA}
settowidth{longA}{xxxxx}
begin{center}
xxxxx
xxxxxhspace{longA}xxxxx
xxxxxhspace{longA}xxxxxhspace{longA}xxxxx
xxxxxhspace{longA}xxxxx
xxxxx
end{center}

120. 112 CAP´ITULO 8. ELEMENTOS DE PROGRAMACI ´ON
xxxxx
xxxxx xxxxx
xxxxx xxxxx xxxxx
xxxxx xxxxx
xxxxx
8.3.1. Longitudes el´asticas fil
En este apartado describiremos dos unidades de longitud el´asticas:
• fil • fill
que LATEX utiliza para introducir espacios de longitud variable. Ambas pro-
porcionan dos diferentes grados de “elasticidad infinita”; fil es una unidad de
longitud el´astica infinitamente m´as grande que cualquier longitud r´ıgida, mien-
tras que fill es infinitamente m´as grande que fil (y por tanto, que cualquier
longitud r´ıgida).
Basados en ´estas unidades de longitud, existe una variedad de comandos:
fill Es una longitud, de valor 0pt plus 1fill.
stretch{n} Es una longitud de valor 0pt y holgura un n´umero n de
unidades fill (entero o decimal). As´ı, fill equivale a stretch{1}.
De ´este modo, los comandos hfill y vfill equivalen a hspace{fill}
y vspace{fill}, respectivamente. La utilidad del comando stretch{n}
est´a en la posibilidad de separar objetos con espacios proporcionales a
diversas cantidades. V´ease el siguiente ejemplo:
Colocamos un texto centrado:[2mm]
vrulehspace{stretch{1}}Texto
centradohspace{stretch{1}}vrulepar
Ahora colocamos un texto con el doble de espacio a
un lado que al otro:par
noindentvrulehspace{stretch{1}}%
Textohspace{stretch{2}}vrulepar
Otro ejemplo, con la distancia entre T1 y T2 igual a
tres veces la distancia a los m’{a}rgenes:par
noindentvrulehspace{stretch{1}}
T1hspace{stretch{3}}T2 hspace{stretch{1}}vrule
Colocamos un texto centrado:

121. 8.3. LONGITUDES 113
Texto centrado
Ahora colocamos un texto con el doble de espacio a un lado que al otro:
Texto
Otro ejemplo, con la distancia entre T1 y T2 igual a tres veces la distancia
a los m´argenes:
T1 T2
(para imprimir la barra vertical de referencia al comienzo y final de l´ınea
en el ejemplo anterior, hemos utilizado el comando vrule; podemos
poner una “marca” en blanco con los comandos mbox{} o null).
hfill y vfill (ya descritos).
hfil y vfil An´alogos a los anteriores, pero empleando para la elasti-
cidad una unidad fil en lugar de fill.
El siguiente ejemplo ilustra la diferencia entre las unidades fil y fill:
noindent A hfil B hfil C
D hfill E hfill F par
A B C
D E F
¿Por qu´e cambian las posiciones de B y C en la primera l´ınea? La respues-
ta est´a en que, antes de cortar una l´ınea, LATEX introduce un espacio de
elasticidad variable, a fin de evitar que las l´ıneas cortas se estiren hacia la
derecha. ´Este espacio se controla a trav´es de la longitud parfillskip,
que por defecto tiene el valor 0pt plus 1fil. Por tanto, en el primer ejem-
plo se equilibran los espacios asociados a tres comandos hfil. En el
segundo caso, esto no sucede, dado que hfill corresponde a un grado
de elasticidad infinitamente m´as grande.
hfilneg y vfilneg Equivalen, respectivamente, a
hspace{0pt plus -1fil} y a vspace{0pt plus -1fil}, y permiten
cancelar el efecto de los comandos hfil y vfil; por ejemplo:
parindent=0pt parfillskip=0pt
newcommand*{centrar}[1]{vrulehfil #1hfilvrule}
centrar{Centrado}par
centrar{Centrado anuladohfilneg}par
centrar{hfilneg Centrado anulado}
Centrado
Centrado anulado
Centrado anulado

122. 114 CAP´ITULO 8. ELEMENTOS DE PROGRAMACI ´ON
hss Equivale a hspace{0pt plus 1fil minus 1fil}, e interviene en
la definici´on de los comandos leftline, rightline y centerline.
vss An´alogo vertical, equivale a vspace{0pt plus 1fil minus 1fil}.
Los siguientes comandos (algunos de ellos ya mencionados anteriormen-
te) tienen un efecto similar a hfill, con la diferencia de que en el espacio
intermedio introducen diversos s´ımbolos de extensi´on variable (en direcci´on
horizontal)
hrulefill
Ahrulefill Bhrulefill C
A B C
dotfill
Adotfill Bdotfill C
A. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .B. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .C
downbracefill y upbracefill Llaves hacia abajo o hacia arriba, res-
pectivamente.
leftarrowfill y rightarrowfill Flechas a izquierda y derecha, res-
pectivamente.
parindent=0pt parfillskip=0pt
mbox{}hspace{stretch{1}}A%
hspace{stretch{3}}mbox{}[-3pt]
mbox{}downbracefillmbox{}%
hspace{stretch{2.3}}mbox{}
Bhspace{stretch{1}}C%
hspace{stretch{1}}D[-7pt]
mbox{}hspace{stretch{2.3}}%
mbox{}upbracefillmbox{}
mbox{}hspace{stretch{1}}E%
hspace{stretch{2}}F%
hspace{stretch{1}}mbox{}[-5pt]
mbox{}hspace{stretch{0.5}}%
rightarrowfill%
hspace{stretch{0.5}}mbox{}

123. 8.3. LONGITUDES 115
A
B C D
E F
−−−−−−−−−−−−−−−−−−−−−−−−−−−→
Antes de continuar es preciso reasignar los valores por defecto a:
parfillskip (para evitar que las l´ıneas cortas se estiren a la derecha), esto es
parfillskip=0pt plus 1fil y tambi´en a parindent (para que se sangre
autom´aticamente el inicio de cualquier p´arrafo), esto es parindent=18pt
Finalmente, describiremos los comandos rlap{Objeto} y llap{Objeto};
respectivamente, colocan Objeto en una caja de anchura 0pt (por lo que el
cursor no se mueve), con el objeto saliendo hacia la derecha o izquierda de la
caja. Por ejemplo:
Tachamos la palabra izquierda%
llap{rule[2.5pt]{48pt}{0.4pt}}
y seguimos escribiendo.par
hfil rlap{uno}llap{dos}vrule par
hfil llap{dos}rlap{uno}vrule
Tachamos la palabra izquierda y seguimos escribiendo.
unodos
dosuno

124. Cap´ıtulo 9
Personalizaciones
9.1. El paquete titlesec
Mediante el paquete titlesec es posible cambiar de forma libre el aspecto de
las unidades de estructura (cap´ıtulo, secciones, subsecciones, etc.) dentro de
un documento. Para ello, se utiliza el comando titleformat (que deber´ıamos
declarar en el pre´ambulo) con el siguiente formato:
titleformat{Comando de Estructura}[Tipo]{Formato}
{Etiqueta}{Separaci´on}{C´odigo anterior}[C´odigo posterior]
Donde cada una de las opciones del comando tiene los siguientes significa-
dos:
Comando de Estructura: El comando para la unidad de estructura cuyo
formato deseamos cambiar; e.g., chapter, section, etc. En algunos
casos es preciso, por ejemplo, usar las formas (ver c´odigo correspondiente
a la Fig. 9.4):
name=chapter
para personalizar la unidad de estructura cap´ıtulo numerado. Y
name=chapter,numberless
para personalizar la unidad de estructura cap´ıtulo no numerado. Algo
similar se puede aplicar a section, etc.
116

125. 9.1. EL PAQUETE TITLESEC 117
Tipo: La forma b´asica para el encabezamiento de la unidad de estructura;
se dispone de las siguientes opciones:
• hang: Pone la etiqueta y el texto del t´ıtulo en la misma l´ınea.
• display: Pone la etiqueta y el texto del t´ıtulo en l´ıneas separadas.
• runing: Integra el t´ıtulo de secci´on dentro de la primera l´ınea del
p´arrafo que comienza la secci´on (no aplica a cap´ıtulo).
• frame: Similar a display pero encuadrando el t´ıtulo.
• leftmargin y rightmargin Colocan el t´ıtulo en los m´argenes de-
recho e izquierdo respectivamente.
• block: Formato general que trata al conjunto etiqueta + t´ıtulo como
un bloque. Preferible a hang para t´ıtulos centrados.
• drop y wrap: Se encaja el t´ıtulo en el primer p´arrafo, ocupando dos
l´ıneas. drop usa una longitud fija para el t´ıtulo y wrap es capaz de
partirlo en dos l´ıneas.
Formato: Comandos y declaraciones que se aplican tanto a la etiqueta
como al texto.
Etiqueta: Identificador asignado al cap´ıtulo, secci´on, etc.
Separaci´on: Longitud de separaci´on entre etiqueta y t´ıtulo de la secci´on;
dependiendo del formato, puede ser una distancia vertical u horizonal.
C´odigo anterior: C´odigo ejecutado inmediatamente antes de la escritura
del t´ıtulo; podemos jugar, como se ha visto en ejemplos anteriores, inclu-
yendo un comando dependiente de un argumento; en el argumento (que
no especificamos) se pasa el t´ıtulo de la secci´on.
C´odigo posterior: C´odigo opcional a ejecutar inmediatamente despu´es
de la escritura del t´ıtulo, que puede ser ejecutado en modo vertical u
horizontal dependiendo del formato del t´ıtulo.
9.1.1. Resultado por defecto
La figura 9.1 muestra el aspecto, por defecto, de las unidades de estructura.
9.1.2. Personalizaci´on tesis fc-unp
Es importante mencionar que en las opciones del comando titleformat po-
demos utilizar los comandos filcenter, filright y filleft para justifi-

126. 118 CAP´ITULO 9. PERSONALIZACIONES
Cap´ıtulo 1
Introducci´on al an´alisis
1.1. N´umeros reales. Conjuntos. L´ogica simb´oli-
ca
1.1.1. Concepto de n´umero real
Por el curso de la escuela secundaria sabemos que todo n´umero real no
negativo x se representa mediante una fracci´on decimal infinita
x , x1x2 . . . , (1.1)
donde x es el n´umero entero mayor que no sobrepasa x y se denomina parte
entera del n´umero x, xn ∈ {0, 1, 2, . . . , 9} para cualquier n ∈ N.
En este caso, las fracciones en las cuales xn = 9 para todo n ≥ n0 (n0 es
cierto n´umero natural) se excluyen com´unmente de la consideraci´on en virtud
de las siguientes igualdades:
x , 999 . . . = x + 1,
x , x1x2 . . . xn0−1999 . . . = x , . . .
. . . (xn0−1 + 1) (n0 > 1, xn0−1 = 9) .
Un n´umero real x es racional, es decir, puede ser representado en forma de
la raz´on m
n
, m, n ∈ Z cuando, y s´olo cuando, la fracci´on 1.1 es peri´odica. En
el caso contrario el n´umero x es irracional.
Se llama valor absoluto o m´odulo del n´umero real x un n´umero no negativo
|x| =
x, si x ≥ 0,
−x, si x < 0.
Se supone que las reglas de comparaci´on de los n´umeros reales, como tam-
bi´en las operaciones aritm´eticas sobre los mismos se conocen por el curso de
ense˜nanza secundaria.
1
Figura 9.1: Aspecto, por defecto, de las unidades de estructura.

127. 9.1. EL PAQUETE TITLESEC 119
car tanto el texto del t´ıtulo como la etiqueta (o los dos globalmente) al centro,
derecha o izquiera, respectivamente.
La figura 9.2 muestra el aspecto de las unidades de estructura obtenido el
siguiente c´odigo:
usepackage{titlesec}
titleformat
{chapter}%Comando de Estructura
[display]%Tipo
{bfseriesLargefilcenter}%Formato
{MakeUppercase{chaptername};Roman{chapter}}%Etiqueta
{25pt}%Separaci´on
{MakeUppercase}%C´odigo anterior
[thispagestyle{empty}]%C´odigo posterior
titleformat
{section}%Comando de Estructura
[hang]%Tipo
{bfserieslarge}%Formato
{arabic{chapter}.arabic{section}.}%Etiqueta
{1em}%Separaci´on
{}%C´odigo anterior
titleformat
{subsection}%Comando de Estructura
[hang]%Tipo
{bfseries}%Formato
{arabic{chapter}.arabic{section}.arabic{subsection}.}%Etiq.
{1em}%Separaci´on
{}%C´odigo anterior
9.1.3. Personalizaci´on titlerule
Para dibujar l´ıneas horizontales se dispone del comando titlerule[grosor];
´este comando dispone de la versi´on con asterisco titlerule*{objeto}, que
permite dibujar copias repetidas de un objeto dado. El comando
titleline[justificaci´on]{material} permite introducir material horizontal
en argumentos de titleformat que esperan material vertical (el par´ame-
tro optativo justificaci´on admite los valores habituales r, l, c). La variante

128. 120 CAP´ITULO 9. PERSONALIZACIONES
CAP´ITULO I
INTRODUCCI´ON AL AN´ALISIS
1.1. N´umeros reales. Conjuntos. L´ogica simb´olica
1.1.1. Concepto de n´umero real
Por el curso de la escuela secundaria sabemos que todo n´umero real no
negativo x se representa mediante una fracci´on decimal infinita
x , x1x2 . . . , (1.1)
donde x es el n´umero entero mayor que no sobrepasa x y se denomina parte
entera del n´umero x, xn ∈ {0, 1, 2, . . . , 9} para cualquier n ∈ N.
En este caso, las fracciones en las cuales xn = 9 para todo n ≥ n0 (n0 es
cierto n´umero natural) se excluyen com´unmente de la consideraci´on en virtud
de las siguientes igualdades:
x , 999 . . . = x + 1,
x , x1x2 . . . xn0−1999 . . . = x , . . .
. . . (xn0−1 + 1) (n0 > 1, xn0−1 = 9) .
Un n´umero real x es racional, es decir, puede ser representado en forma de
la raz´on m
n
, m, n ∈ Z cuando, y s´olo cuando, la fracci´on (1.1) es peri´odica. En
el caso contrario el n´umero x es irracional.
Se llama valor absoluto o m´odulo del n´umero real x un n´umero no negativo
|x| =
x, si x ≥ 0,
−x, si x < 0.
Se supone que las reglas de comparaci´on de los n´umeros reales, como tam-
bi´en las operaciones aritm´eticas sobre los mismos se conocen por el curso de
ense˜nanza secundaria.
Figura 9.2: Aspecto de las unidades de estructura obtenido con la personali-
zaci´on tesis fc-unp.

129. 9.1. EL PAQUETE TITLESEC 121
titleline*[justificaci´on]{material} permite introducir el material en una
caja de anchura titlewidth (variable de longitud que almacena la anchura
del t´ıtulo). Es esencial, a la hora de utilizar ´esta variante, cargar el paquete
titlesec con la opci´on calcwidth en el pre´ambulo.
La figura 9.3 muestra el aspecto de las unidades de estructura obtenido con
el siguiente c´odigo:
usepackage[T1]{fontenc}
usepackage[calcwidth]{titlesec}
usepackage{anyfontsize}
titleformat
{chapter}%Comando de Estructura
[display]%Tipo
{filcenterbfseriesLARGE}%Formato
{largescshapechaptername;thechapter}%Etiqueta
{0ex}%Separaci´on
{titleline*[c]{titlerule}vspace{6pt}%
titleline*[c]{titlerule*{tiny$diamond$}}%
vspace{6pt}}%C´odigo anterior
[{vspace{6pt}%
titleline*[c]{titlerule*{tiny$diamond$}}%
vspace{6pt}%
titleline*[c]{titlerule}}]%C´odigo posterior
titleformat
{section}%Comando de Estructura
[hang]%Tipo
{bfseriesfontsize{16}{16}selectfont}%Formato
{thesection.}%Etiqueta
{1em}%Separaci´on
{}%C´odigo anterior
9.1.4. Personalizaci´on leftmarg
Para especificar una indentaci´on arbitraria en los distintos elementos del t´ıtulo,
se utiliza el comando:
titlespacing{Comando de estructura}{Indentaci´on Izq.}
{Espacio anterior}{Espacio posterior}[Indentaci´on Der.]

130. 122 CAP´ITULO 9. PERSONALIZACIONES
Capítulo 1
Introducción al análisis
1.1. Números reales. Conjuntos. Lógica simbólica
1.1.1. Concepto de número real
Por el curso de la escuela secundaria sabemos que todo número real no
negativo x se representa mediante una fracción decimal innita
x , x1x2 . . . , (1.1)
donde x es el número entero mayor que no sobrepasa x y se denomina parte
entera del número x, xn ∈ {0, 1, 2, . . . , 9} para cualquier n ∈ N.
En este caso, las fracciones en las cuales xn = 9 para todo n ≥ n0 (n0 es
cierto número natural) se excluyen comúnmente de la consideración en virtud
de las siguientes igualdades:
x , 999 . . . = x + 1,
x , x1x2 . . . xn0−1999 . . . = x , . . .
. . . (xn0−1 + 1) (n0 1, xn0−1 = 9) .
Un número real x es racional, es decir, puede ser representado en forma de
la razón m
n
, m, n ∈ Z cuando, y sólo cuando, la fracción (1.1) es periódica. En
el caso contrario el número x es irracional.
Se llama valor absoluto o módulo del número real x un número no negativo
|x| =
x, si x ≥ 0,
−x, si x 0.
Se supone que las reglas de comparación de los números reales, como tam-
bién las operaciones aritméticas sobre los mismos se conocen por el curso de
enseñanza secundaria.
1
Figura 9.3: Aspecto de las unidades de estructura obtenido con la personali-
zaci´on titlerule.

131. 9.1. EL PAQUETE TITLESEC 123
donde las opciones de Indentaci´on Izq. o Indentaci´on Der. se pueden utilizar
para cambiar la anchura y colocaci´on del t´ıtulo, y las opciones de Espacio
anterior y Espacio posterior especifican los espacios a dejar antes y despu´es
del t´ıtulo, respectivamente. ´Estas longitudes, cuando son de tipo el´astico, se
especifican a trav´es de la declaraci´on *f (siendo f un factor decimal), lo cual
equivale a f unidades ex con una cierta elasticidad.
La figura 9.4 muestra el aspecto de las unidades de estructura obtenido con
el siguiente c´odigo:
usepackage{titlesec}
usepackage{anyfontsize}
titleformat
{chapter}%Comando de Estructura
{sffamilybfseriesHuge}%Formato
{llap{makebox[2em][r]{thechapter}hspace{1em}}}%Etiqueta
{0pt}%Separaci´on
{}%C´odigo anterior
titleformat
{section}%Comando de Estructura
[leftmargin]%Tipo
{filcentersffamilybfserieslarge}%Formato
{thesection}%Etiqueta
{0pt}%Separaci´on
{}%C´odigo anterior
titlespacing{section}{2.5cm}{*2.5}{0.5cm}
titleformat
{subsection}%Comando de Estructura
[hang]%Tipo
{sffamilybfseries}%Formato
{thesubsection}%Etiqueta
{1em}%Separaci´on
{}%C´odigo anterior
9.1.5. Personalizaci´on tikz
La figura 9.5 muestra el aspecto de las unidades de estructura obtenido con el
siguiente c´odigo:

132. 124 CAP´ITULO 9. PERSONALIZACIONES
1 Introducci´on al an´alisis
1.1
N´umeros
reales.
Conjuntos.
L´ogica
simb´olica
1.1.1 Concepto de n´umero real
Por el curso de la escuela secundaria sabemos que todo n´umero real no
negativo x se representa mediante una fracci´on decimal infinita
x , x1x2 . . . , (1.1)
donde x es el n´umero entero mayor que no sobrepasa x y se denomina parte
entera del n´umero x, xn ∈ {0, 1, 2, . . . , 9} para cualquier n ∈ N.
En este caso, las fracciones en las cuales xn = 9 para todo n ≥ n0 (n0 es
cierto n´umero natural) se excluyen com´unmente de la consideraci´on en virtud
de las siguientes igualdades:
x , 999 . . . = x + 1,
x , x1x2 . . . xn0−1999 . . . = x , . . .
. . . (xn0−1 + 1) (n0 1, xn0−1 = 9) .
Un n´umero real x es racional, es decir, puede ser representado en forma de
la raz´on m
n
, m, n ∈ Z cuando, y s´olo cuando, la fracci´on (1.1) es peri´odica. En
el caso contrario el n´umero x es irracional.
Se llama valor absoluto o m´odulo del n´umero real x un n´umero no negativo
|x| =
x, si x ≥ 0,
−x, si x 0.
Se supone que las reglas de comparaci´on de los n´umeros reales, como tam-
bi´en las operaciones aritm´eticas sobre los mismos se conocen por el curso de
ense˜nanza secundaria.
1
Figura 9.4: Aspecto de las unidades de estructura obtenido con la personali-
zaci´on leftmarg.

133. 9.1. EL PAQUETE TITLESEC 125
usepackage{titlesec}
usepackage{anyfontsize}
newcommand{myfontsize}[1]{fontsize{#1}{#1}selectfont}
usepackage{tikz}
newcommand{backgr}{%
begin{tikzpicture}[overlay,%
baseline={([yshift=-5pt]current bounding box.north)}]%
draw[line width=8ex,SteelBlue]%
(-paperwidth,0ex)--(paperwidth,0ex);
end{tikzpicture}
}
newlength{myskip}
makeatletter
setlength{myskip}{f@size pt}
makeatother
newcommand{nodechap}{%
rule{0.1textwidth}{0pt}
begin{tikzpicture}[overlay,%
baseline={([yshift=-5pt]current bounding box.north)}]%
node[minimum width=10ex,minimum height=10ex,draw=Black]%
{myfontsize{8myskip}thechapter};
end{tikzpicture}%
}
newcommand{titlechap}[1]{%
rule{0.05textwidth}{0pt}
parbox[c]{0.8textwidth}{textcolor{white}{#1}}%
}
titleformat
{name=chapter}%C. de Estructura (cap. numer.)
[hang]%Tipo
{bfseriesLARGE
}%Formato
{backgrnodechap}%Etiqueta
{1em}%Separaci´on
{titlechap}%C´odigo anterior
[thispagestyle{empty}]%C´odigo posterior

134. 126 CAP´ITULO 9. PERSONALIZACIONES
titleformat
{name=chapter,numberless}%C. de Estructura (cap. no numer.)
[hang]%Tipo
{bfseriesLARGE}%Formato
{backgr}%Etiqueta
{1em}%Separaci´on
{titlechap}%C´odigo anterior
[thispagestyle{empty}]%C´odigo posterior
titlespacing{chapter}{-5ex}{7ex}{20ex}
newcommand{nodesec}{%
begin{tikzpicture}[%
baseline={([yshift=-5.5pt]current bounding box.center)}]
node[draw=Black]{textcolor{SteelBlue}{thesection}};
end{tikzpicture}%
}
newcommand{titlesec}[1]{%
textcolor{SteelBlue}{#1}%
}
titleformat
{section}%Comando de Estructura
[hang]%Tipo
{bfserieslarge}%Formato
{nodesec}%Etiqueta
{0.5em}%Separaci´on
{titlesec}%C´odigo anterior
newcommand{titlesubsec}[1]{%
textcolor{SteelBlue}{#1}%
}
titleformat
{subsection}%Comando de Estructura
[hang]%Tipo
{bfseries}%Formato
{textcolor{SteelBlue}{thesubsection}}%Etiqueta
{0.5em}%Separaci´on
{titlesubsec}%C´odigo anterior

135. 9.2. EL PAQUETE FACYHDR 127
Observaciones.
1. El lector debe tener en cuenta que en este caso es preciso a˜nadir la opci´on
svgnames al comando documentclass para que sean reconocidos los
nombres de colores: Black y SteelBlue; y as´ı obtener un resultado sin
errores, como el que se muestra en la figura 9.5. En este ejemplo se us´o el
c´odigo:
documentclass[12pt,a4paper,svgnames]{book}
al inicio del documento.
2. Otra capacidad interesante del paquete es la especificaci´on condicional
de formatos de t´ıtulo para p´aginas pares o impares, utilizando la variable
page (con valores even u odd) en la opci´on comando de estructura. Para
que ´esto funcione, es importante que el manuscrito est´e formateado con
la opci´on twoside.
9.2. El paquete facyhdr
El paquete fancyhdr permite modificar encabezamientos y pies de p´agina.
Existen dos comandos ´utiles para definir los encabezamientos y los pies de
p´aginas:
fancyhead{texto}
fancyfoot{texto}.
A estos comandos se les puede pasar unos selectores que indican en que par-
te del encabezado/pie de p´agina se escribir´an: L (izquierda), C (centro) y R
(derecha). Adem´as para libros se puede hacer que las p´aginas impares sean
diferentes de las p´aginas pares. Para ello se utilizan los selectores: E (par) y O
(impar).
9.2.1. Resultado por defecto
Las figuras 9.6 y 9.7 muestran el aspecto, por defecto, de los encabezados y
pies de p´agina.

136. 128 CAP´ITULO 9. PERSONALIZACIONES
1 Introducci´on al an´alisis
1.1 N´umeros reales. Conjuntos. L´ogica simb´olica
1.1.1 Concepto de n´umero real
Por el curso de la escuela secundaria sabemos que todo n´umero real no
negativo x se representa mediante una fracci´on decimal infinita
x , x1x2 . . . , (1.1)
donde x es el n´umero entero mayor que no sobrepasa x y se denomina parte
entera del n´umero x, xn ∈ {0, 1, 2, . . . , 9} para cualquier n ∈ N.
En este caso, las fracciones en las cuales xn = 9 para todo n ≥ n0 (n0 es
cierto n´umero natural) se excluyen com´unmente de la consideraci´on en virtud
de las siguientes igualdades:
x , 999 . . . = x + 1,
x , x1x2 . . . xn0−1999 . . . = x , . . .
. . . (xn0−1 + 1) (n0 1, xn0−1 = 9) .
Un n´umero real x es racional, es decir, puede ser representado en forma de
la raz´on m
n
, m, n ∈ Z cuando, y s´olo cuando, la fracci´on (1.1) es peri´odica. En
el caso contrario el n´umero x es irracional.
Se llama valor absoluto o m´odulo del n´umero real x un n´umero no negativo
|x| =
x, si x ≥ 0,
−x, si x 0.
Se supone que las reglas de comparaci´on de los n´umeros reales, como tam-
bi´en las operaciones aritm´eticas sobre los mismos se conocen por el curso de
ense˜nanza secundaria.
Figura 9.5: Aspecto de las unidades de estructura obtenido con la personali-
zaci´on tikz.

137. 9.2. EL PAQUETE FACYHDR 129
2 CAP´ITULO 1. INTRODUCCI ´ON AL AN ´ALISIS
1.2. Conjuntos y operaciones sobre ellos
Por conjunto se entiende cualquier totalidad de objetos, llamados elementos
del conjunto.
La notaci´on a ∈ A significa que el objeto a es un elemento del conjunto A
(pertenece al conjunto A); en el caso contrario se escribe a ∈ A. Un conjunto
que no contiene ning´un elemento, se denomina vac´ıo y se designa por el s´ımbolo
∅. La notaci´on A ⊂ B (A est´a contenido en B) quiere decir que todo elemento
del conjunto A es un elemento del conjunto B; en este caso el conjunto A
lleva el nombre de subconjunto del conjunto B. Los conjuntos A y B se llaman
iguales (A = B), si A ⊂ B y B ⊂ A.
Existen dos m´etodos principales para definir (escribir)los conjuntos.
1. El conjunto A se determina por enumeraci´on directa de todos sus ele-
mentos a1, a2, . . . , an, es decir, se escribe en la forma
A = {a1, a2, . . . , an}.
2. El conjunto A se determina como una totalidad de aquellos y s´olo aque-
llos, elementos de cierto conjunto b´asico T, que poseen la propiedad
com´un α. En este caso se emplea la designaci´on
A = {x ∈ T|α(x)},
donde la notaci´on α(x) significa que el elemento x posee la propiedad α.
1.3. Cotas superiores e inferiores
Sea X un conjunto arbitrario no vac´ıo de n´umeros reales. El n´umero M =
m´ax X se denomina elemento mayor (maximal) del conjunto X, si M ∈ X y
para todo x ∈ X se verifica la desigualdad x ≤ M. An´alogamente se determina
el concepto de elemento menor (minimal) m = m´ın X del conjunto X.
El conjunto x se llama acotado superiormente, si existe un n´umero real a
de tal ´ındole que x ≤ a para cualquier x ∈ X. Todo n´umero que posee dicha
propiedad lleva el nombre de cota superior del conjunto X. Para el conjunto
dado X acotado superiormente, el conjunto de todas las cotas superiores tiene
un elemento menor, que se denomina cota superior exacta del conjunto X y se
designa mediante el s´ımbolo sup X.
An´alogamente se determinan los conceptos de conjunto acotado inferior-
mente, de cota inferior y de cota inferior exacta del conjunto X; esta ´ultima
se designa mediante el s´ımbolo ´ınf X.
El conjunto X se denomina acotado, si est´a acotado superior e inferiormen-
te.
Figura 9.6: Encabezado y pie de p´agina, por defecto, en una p´agina par.

138. 130 CAP´ITULO 9. PERSONALIZACIONES
1.4. L ´OGICA SIMB ´OLICA 3
1.4. L´ogica simb´olica
Al anotar los razonamientos matem´aticos resulta razonable aplicar ciertos
s´ımbolos econ´omicos usados en la l´ogica. He aqu´ı algunos s´ımbolos de los m´as
sencillos utilizados con mayor frecuencia.
Sean α, β ciertas declaraciones o afirmaciones, es decir, oraciones narrato-
rias, con respecto a cada una de las cuales podemos decir si es cierta o falsa.
la notaci´on α significa: “no α”, es decir, negaci´on de la afirmaci´on α.
La notaci´on α ⇒ β significa: “de la afirmaci´on α resulta la afirmaci´on β”
(⇒ es el s´ımbolo de implicaci´on).
La notaci´on α ⇔ β significa: “la afirmaci´on α es equivalente a la afirma-
ci´on β”, es decir, de α proviene β y de β se deduce α (⇔ es el s´ımbolo de
equivalencia).
La notaci´on α ∧ β significa: “α y β” (∧ es el s´ımbolo de conjunci´on).
La notaci´on α ∨ β significa: “α ´o β” (∨ es el s´ımbolo de disyunci´on).
La notaci´on
∀x ∈ Xα(x)
significa: “para todo elemento x ∈ X la afirmaci´on α(x) es ver´ıdica” (∀ es el
cuantificador universal).
La notaci´on
∃x ∈ Xα(x)
significa: “existe tal elemento x ∈ X, para el cual la afirmaci´on α(x) es ver´ıdi-
ca” (∃ es el cuantificador existencial).
Si un elemento x ∈ X, para el cual la afirmaci´on α(x) es ver´ıdica no s´olo
existe, sino que es ´unico, se escribe:
∃! x ∈ Xα(x).
Figura 9.7: Encabezado y pie de p´agina, por defecto, en una p´agina impar.

139. 9.2. EL PAQUETE FACYHDR 131
9.2.2. Personalizaci´on simple
Las figuras 9.8 y 9.9 muestran el aspecto de los encabezados y pies de p´agina
obtenidos con el siguiente c´odigo:
usepackage{fancyhdr}
pagestyle{fancy}
fancyhf{} % borra todos los campos del encabezado y pie
fancyhead[R]{Universidad Nacional de Piura} %Especifica
%el texto a poner a la derecha del encabezado
fancyfoot[LO,RE]{P´agina thepage} %N´umero de p´agina
%a la izquierda en las p´aginas impares
%y a la derecha en las pares
fancyfoot[LE,RO]{Proyecto Fin de Carrera} %Escribe este
%texto a la izquierda en las p´aginas impares
%y a la derecha en las pares
9.2.3. Personalizaci´on rule
Si se quiere modificar el grosor de las l´ıneas de separaci´on entre encabeza y pie
de p´agina se utiliza:
renewcommand{headrulewidth}{g}
renewcommand{footrulewidth}{g}
Si se desea obligar a que desaparezca una o ambas l´ıneas bastar´a con asignar
el valor 0pt a g.
Las figuras 9.10 y 9.11 muestran el aspecto de los encabezados y pies de
p´agina obtenidos con el siguiente c´odigo:
usepackage{fancyhdr}
pagestyle{fancy}
fancyhf{} % borra todos los campos del encabezado y pie
fancyhead[RO,LE]{bfseries Matem´atica b´asica}

140. 132 CAP´ITULO 9. PERSONALIZACIONES
Universidad Nacional de Piura
1.2. Conjuntos y operaciones sobre ellos
Por conjunto se entiende cualquier totalidad de objetos, llamados elementos
del conjunto.
La notaci´on a ∈ A significa que el objeto a es un elemento del conjunto A
(pertenece al conjunto A); en el caso contrario se escribe a ∈ A. Un conjunto
que no contiene ning´un elemento, se denomina vac´ıo y se designa por el s´ımbolo
∅. La notaci´on A ⊂ B (A est´a contenido en B) quiere decir que todo elemento
del conjunto A es un elemento del conjunto B; en este caso el conjunto A
lleva el nombre de subconjunto del conjunto B. Los conjuntos A y B se llaman
iguales (A = B), si A ⊂ B y B ⊂ A.
Existen dos m´etodos principales para definir (escribir)los conjuntos.
1. El conjunto A se determina por enumeraci´on directa de todos sus ele-
mentos a1, a2, . . . , an, es decir, se escribe en la forma
A = {a1, a2, . . . , an}.
2. El conjunto A se determina como una totalidad de aquellos y s´olo aque-
llos, elementos de cierto conjunto b´asico T, que poseen la propiedad
com´un α. En este caso se emplea la designaci´on
A = {x ∈ T|α(x)},
donde la notaci´on α(x) significa que el elemento x posee la propiedad α.
1.3. Cotas superiores e inferiores
Sea X un conjunto arbitrario no vac´ıo de n´umeros reales. El n´umero M =
m´ax X se denomina elemento mayor (maximal) del conjunto X, si M ∈ X y
para todo x ∈ X se verifica la desigualdad x ≤ M. An´alogamente se determina
el concepto de elemento menor (minimal) m = m´ın X del conjunto X.
El conjunto x se llama acotado superiormente, si existe un n´umero real a
de tal ´ındole que x ≤ a para cualquier x ∈ X. Todo n´umero que posee dicha
propiedad lleva el nombre de cota superior del conjunto X. Para el conjunto
dado X acotado superiormente, el conjunto de todas las cotas superiores tiene
un elemento menor, que se denomina cota superior exacta del conjunto X y se
designa mediante el s´ımbolo sup X.
An´alogamente se determinan los conceptos de conjunto acotado inferior-
mente, de cota inferior y de cota inferior exacta del conjunto X; esta ´ultima
se designa mediante el s´ımbolo ´ınf X.
El conjunto X se denomina acotado, si est´a acotado superior e inferiormen-
te.
Proyecto Fin de Carrera P´agina 2
Figura 9.8: Encabezado y pie de p´agina, en una p´agina par, obtenido con la
personalizaci´on simple.

141. 9.2. EL PAQUETE FACYHDR 133
Universidad Nacional de Piura
1.4. L´ogica simb´olica
Al anotar los razonamientos matem´aticos resulta razonable aplicar ciertos
s´ımbolos econ´omicos usados en la l´ogica. He aqu´ı algunos s´ımbolos de los m´as
sencillos utilizados con mayor frecuencia.
Sean α, β ciertas declaraciones o afirmaciones, es decir, oraciones narrato-
rias, con respecto a cada una de las cuales podemos decir si es cierta o falsa.
la notaci´on α significa: “no α”, es decir, negaci´on de la afirmaci´on α.
La notaci´on α ⇒ β significa: “de la afirmaci´on α resulta la afirmaci´on β”
(⇒ es el s´ımbolo de implicaci´on).
La notaci´on α ⇔ β significa: “la afirmaci´on α es equivalente a la afirma-
ci´on β”, es decir, de α proviene β y de β se deduce α (⇔ es el s´ımbolo de
equivalencia).
La notaci´on α ∧ β significa: “α y β” (∧ es el s´ımbolo de conjunci´on).
La notaci´on α ∨ β significa: “α ´o β” (∨ es el s´ımbolo de disyunci´on).
La notaci´on
∀x ∈ Xα(x)
significa: “para todo elemento x ∈ X la afirmaci´on α(x) es ver´ıdica” (∀ es el
cuantificador universal).
La notaci´on
∃x ∈ Xα(x)
significa: “existe tal elemento x ∈ X, para el cual la afirmaci´on α(x) es ver´ıdi-
ca” (∃ es el cuantificador existencial).
Si un elemento x ∈ X, para el cual la afirmaci´on α(x) es ver´ıdica no s´olo
existe, sino que es ´unico, se escribe:
∃! x ∈ Xα(x).
P´agina 3 Proyecto Fin de Carrera
Figura 9.9: Encabezado y pie de p´agina, en una p´agina impar, obtenido con la
personalizaci´on simple.

142. 134 CAP´ITULO 9. PERSONALIZACIONES
fancyfoot[LE,RO]{thepage} % N´umero de p´agina
%a la izquierda en las p´aginas pares
%y a la derecha en las impares
fancyfoot[CO,CE]{Dpto. Matem´atica - UNP} % Escribe este
%texto al centro en las p´aginas impares
%y al centro en las pares
fancyfoot[LO,RE]{R. Ipanaqu´e} % Escribe este
%texto a la izquierda en las p´aginas impares
%y a la derecha en las pares
renewcommand{headrulewidth}{0.4pt} % Establece una
%l´ınea de 0.4pt de grosor en el encabezado
renewcommand{footrulewidth}{0.4pt} % Establece una
%l´ınea de 0.4pt de grosor en el pie de p´agina
9.2.4. Personalizaci´on actualizable
Existen dos comandos1
´utiles para poder hacer encabezados que cambien seg´un
se avanza en el texto: leftmark (nivel m´as alto) y rightmark (nivel inferior).
Tambi´en es posible modificar la presentaci´on de la informaci´on con respecto
a cap´ıtulos, secciones y subsecciones redefiniendo los comandos
chaptermark, sectionmark y subsectionmark.
Por ejemplo, el dise˜no por defecto, de los encabezados y pies de p´agina en
la clase book, se puede obtener con los siguientes comandos (Figs. 9.6 y 9.7):
usepackage{fancyhdr}
pagestyle{fancy}
renewcommand{chaptermark}[1]{%
markboth{MakeUppercase{chaptername thechapter. #1}}{}}
renewcommand{sectionmark}[1]{%
markright{MakeUppercase{thesection. #1}}}
fancyhead{}
fancyfoot{}
fancyhead[RE]{slshape leftmark}
fancyhead[LO]{slshape rightmark}
1
Su valor depende del tipo de documento.

143. 9.2. EL PAQUETE FACYHDR 135
Matem´atica b´asica
1.2. Conjuntos y operaciones sobre ellos
Por conjunto se entiende cualquier totalidad de objetos, llamados elementos
del conjunto.
La notaci´on a ∈ A significa que el objeto a es un elemento del conjunto A
(pertenece al conjunto A); en el caso contrario se escribe a ∈ A. Un conjunto
que no contiene ning´un elemento, se denomina vac´ıo y se designa por el s´ımbolo
∅. La notaci´on A ⊂ B (A est´a contenido en B) quiere decir que todo elemento
del conjunto A es un elemento del conjunto B; en este caso el conjunto A
lleva el nombre de subconjunto del conjunto B. Los conjuntos A y B se llaman
iguales (A = B), si A ⊂ B y B ⊂ A.
Existen dos m´etodos principales para definir (escribir)los conjuntos.
1. El conjunto A se determina por enumeraci´on directa de todos sus ele-
mentos a1, a2, . . . , an, es decir, se escribe en la forma
A = {a1, a2, . . . , an}.
2. El conjunto A se determina como una totalidad de aquellos y s´olo aque-
llos, elementos de cierto conjunto b´asico T, que poseen la propiedad
com´un α. En este caso se emplea la designaci´on
A = {x ∈ T|α(x)},
donde la notaci´on α(x) significa que el elemento x posee la propiedad α.
1.3. Cotas superiores e inferiores
Sea X un conjunto arbitrario no vac´ıo de n´umeros reales. El n´umero M =
m´ax X se denomina elemento mayor (maximal) del conjunto X, si M ∈ X y
para todo x ∈ X se verifica la desigualdad x ≤ M. An´alogamente se determina
el concepto de elemento menor (minimal) m = m´ın X del conjunto X.
El conjunto x se llama acotado superiormente, si existe un n´umero real a
de tal ´ındole que x ≤ a para cualquier x ∈ X. Todo n´umero que posee dicha
propiedad lleva el nombre de cota superior del conjunto X. Para el conjunto
dado X acotado superiormente, el conjunto de todas las cotas superiores tiene
un elemento menor, que se denomina cota superior exacta del conjunto X y se
designa mediante el s´ımbolo sup X.
An´alogamente se determinan los conceptos de conjunto acotado inferior-
mente, de cota inferior y de cota inferior exacta del conjunto X; esta ´ultima
se designa mediante el s´ımbolo ´ınf X.
El conjunto X se denomina acotado, si est´a acotado superior e inferiormen-
te.
2 Dpto. Matem´atica - UNP R. Ipanaqu´e
Figura 9.10: Encabezado y pie de p´agina, en una p´agina par, obtenido con la
personalizaci´on rule.

144. 136 CAP´ITULO 9. PERSONALIZACIONES
Matem´atica b´asica
1.4. L´ogica simb´olica
Al anotar los razonamientos matem´aticos resulta razonable aplicar ciertos
s´ımbolos econ´omicos usados en la l´ogica. He aqu´ı algunos s´ımbolos de los m´as
sencillos utilizados con mayor frecuencia.
Sean α, β ciertas declaraciones o afirmaciones, es decir, oraciones narrato-
rias, con respecto a cada una de las cuales podemos decir si es cierta o falsa.
la notaci´on α significa: “no α”, es decir, negaci´on de la afirmaci´on α.
La notaci´on α ⇒ β significa: “de la afirmaci´on α resulta la afirmaci´on β”
(⇒ es el s´ımbolo de implicaci´on).
La notaci´on α ⇔ β significa: “la afirmaci´on α es equivalente a la afirma-
ci´on β”, es decir, de α proviene β y de β se deduce α (⇔ es el s´ımbolo de
equivalencia).
La notaci´on α ∧ β significa: “α y β” (∧ es el s´ımbolo de conjunci´on).
La notaci´on α ∨ β significa: “α ´o β” (∨ es el s´ımbolo de disyunci´on).
La notaci´on
∀x ∈ Xα(x)
significa: “para todo elemento x ∈ X la afirmaci´on α(x) es ver´ıdica” (∀ es el
cuantificador universal).
La notaci´on
∃x ∈ Xα(x)
significa: “existe tal elemento x ∈ X, para el cual la afirmaci´on α(x) es ver´ıdi-
ca” (∃ es el cuantificador existencial).
Si un elemento x ∈ X, para el cual la afirmaci´on α(x) es ver´ıdica no s´olo
existe, sino que es ´unico, se escribe:
∃! x ∈ Xα(x).
R. Ipanaqu´e Dpto. Matem´atica - UNP 3
Figura 9.11: Encabezado y pie de p´agina, en una p´agina impar, obtenido con
la personalizaci´on rule.

145. 9.3. EL PAQUETE TITLETOC 137
fancyhead[LE,RO]{thepage}
renewcommand{headrulewidth}{0pt}
Las figuras 9.12 y 9.13 muestran el aspecto de los encabezados y pies de
p´agina obtenidos con el siguiente c´odigo:
usepackage{fancyhdr}
pagestyle{fancy}
renewcommand{chaptermark}[1]%
{markboth{MakeUppercase{thechapter. #1}}{}}
renewcommand{sectionmark}[1]%
{markright{MakeUppercase{thesection. #1}}}
renewcommand{headrulewidth}{0.5pt}
renewcommand{footrulewidth}{0.5pt}
newcommand{helv}{%
fontfamily{phv}fontseries{b}fontsize{9}{11}selectfont}
fancyhf{}
fancyhead[LE,RO]{helv thepage}
fancyhead[LO]{helv rightmark}
fancyhead[RE]{helv leftmark}
fancyfoot[RO,LE]{helv UNP}
fancyfoot[RE,LO]{%
vspace{-2ex}includegraphics[scale=0.075]{unp}%
}
9.3. El paquete titletoc

146. 138 CAP´ITULO 9. PERSONALIZACIONES
2 1. INTRODUCCI ´ON AL AN ´ALISIS
1.2. Conjuntos y operaciones sobre ellos
Por conjunto se entiende cualquier totalidad de objetos, llamados elementos
del conjunto.
La notaci´on a ∈ A significa que el objeto a es un elemento del conjunto A
(pertenece al conjunto A); en el caso contrario se escribe a ∈ A. Un conjunto
que no contiene ning´un elemento, se denomina vac´ıo y se designa por el s´ımbolo
∅. La notaci´on A ⊂ B (A est´a contenido en B) quiere decir que todo elemento
del conjunto A es un elemento del conjunto B; en este caso el conjunto A
lleva el nombre de subconjunto del conjunto B. Los conjuntos A y B se llaman
iguales (A = B), si A ⊂ B y B ⊂ A.
Existen dos m´etodos principales para definir (escribir)los conjuntos.
1. El conjunto A se determina por enumeraci´on directa de todos sus ele-
mentos a1, a2, . . . , an, es decir, se escribe en la forma
A = {a1, a2, . . . , an}.
2. El conjunto A se determina como una totalidad de aquellos y s´olo aque-
llos, elementos de cierto conjunto b´asico T, que poseen la propiedad
com´un α. En este caso se emplea la designaci´on
A = {x ∈ T|α(x)},
donde la notaci´on α(x) significa que el elemento x posee la propiedad α.
1.3. Cotas superiores e inferiores
Sea X un conjunto arbitrario no vac´ıo de n´umeros reales. El n´umero M =
m´ax X se denomina elemento mayor (maximal) del conjunto X, si M ∈ X y
para todo x ∈ X se verifica la desigualdad x ≤ M. An´alogamente se determina
el concepto de elemento menor (minimal) m = m´ın X del conjunto X.
El conjunto x se llama acotado superiormente, si existe un n´umero real a
de tal ´ındole que x ≤ a para cualquier x ∈ X. Todo n´umero que posee dicha
propiedad lleva el nombre de cota superior del conjunto X. Para el conjunto
dado X acotado superiormente, el conjunto de todas las cotas superiores tiene
un elemento menor, que se denomina cota superior exacta del conjunto X y se
designa mediante el s´ımbolo sup X.
An´alogamente se determinan los conceptos de conjunto acotado inferior-
mente, de cota inferior y de cota inferior exacta del conjunto X; esta ´ultima
se designa mediante el s´ımbolo ´ınf X.
El conjunto X se denomina acotado, si est´a acotado superior e inferiormen-
te.
UNP
Figura 9.12: Encabezado y pie de p´agina, en una p´agina par, obtenido con la
personalizaci´on actualizable.

147. 9.3. EL PAQUETE TITLETOC 139
1.4. L ´OGICA SIMB ´OLICA 3
1.4. L´ogica simb´olica
Al anotar los razonamientos matem´aticos resulta razonable aplicar ciertos
s´ımbolos econ´omicos usados en la l´ogica. He aqu´ı algunos s´ımbolos de los m´as
sencillos utilizados con mayor frecuencia.
Sean α, β ciertas declaraciones o afirmaciones, es decir, oraciones narrato-
rias, con respecto a cada una de las cuales podemos decir si es cierta o falsa.
la notaci´on α significa: “no α”, es decir, negaci´on de la afirmaci´on α.
La notaci´on α ⇒ β significa: “de la afirmaci´on α resulta la afirmaci´on β”
(⇒ es el s´ımbolo de implicaci´on).
La notaci´on α ⇔ β significa: “la afirmaci´on α es equivalente a la afirma-
ci´on β”, es decir, de α proviene β y de β se deduce α (⇔ es el s´ımbolo de
equivalencia).
La notaci´on α ∧ β significa: “α y β” (∧ es el s´ımbolo de conjunci´on).
La notaci´on α ∨ β significa: “α ´o β” (∨ es el s´ımbolo de disyunci´on).
La notaci´on
∀x ∈ Xα(x)
significa: “para todo elemento x ∈ X la afirmaci´on α(x) es ver´ıdica” (∀ es el
cuantificador universal).
La notaci´on
∃x ∈ Xα(x)
significa: “existe tal elemento x ∈ X, para el cual la afirmaci´on α(x) es ver´ıdi-
ca” (∃ es el cuantificador existencial).
Si un elemento x ∈ X, para el cual la afirmaci´on α(x) es ver´ıdica no s´olo
existe, sino que es ´unico, se escribe:
∃! x ∈ Xα(x).
UNP
Figura 9.13: Encabezado y pie de p´agina, en una p´agina impar, obtenido con
la personalizaci´on actualizable.

148. Bibliograf´ıa
[1] Aranda, E. CURSO DE LATEX. Departamento de Matem´aticas, E.T.S. In-
genieros Industriales, Universidad de Castilla, La Mancha. http://www.
wiphala.net/courses/tools/latex/KAS_LATEX/2008-I (2008).
[2] Cubides, C., Rojas, A. y Pardo, C. CURSO B´ASICO DE LATEX. http:
//www.emis.de/journals/RCE/IntroLatex (2006).
[3] Griffiths, D and Higham, D. LEARNING LATEX. The Society for Industrial
and Applied Mathematics (1997).
[4] Gurari, E. WRITING WITH TEX. McGraw-Hill, Inc. (1994).
[5] Knuth, D. THE TEXBOOK. Adisson-Wesley Publishing Company (1991).
140