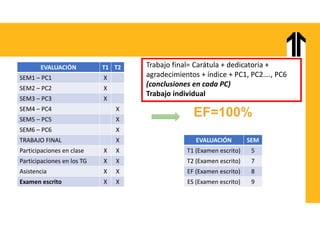
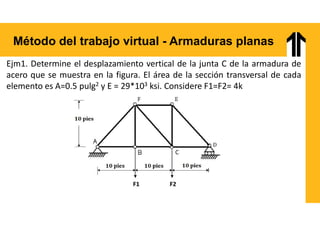
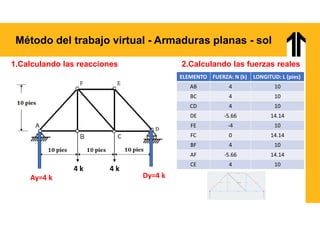
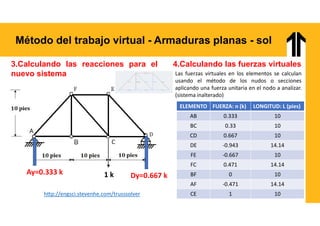
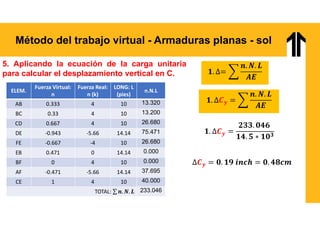
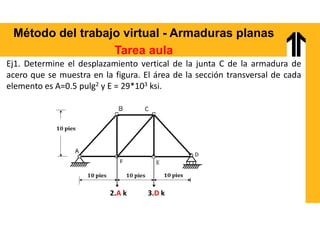
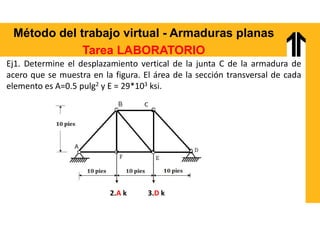
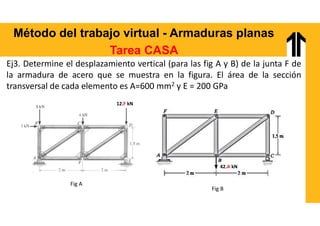
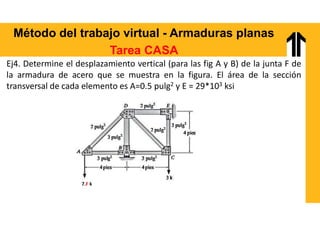
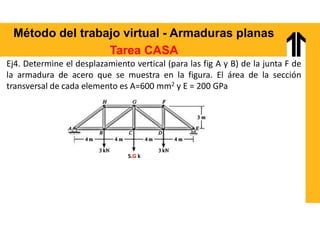
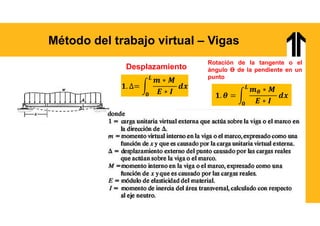
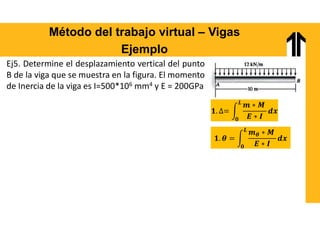
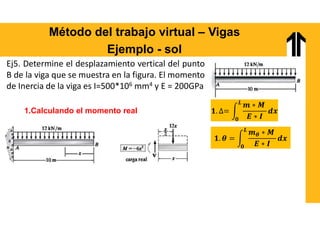
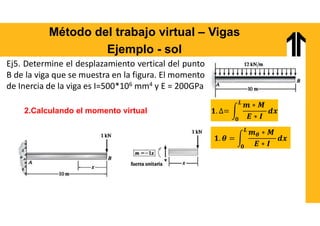
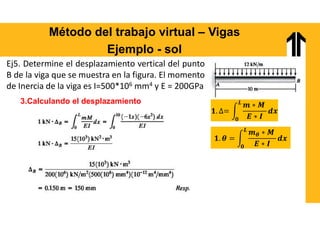
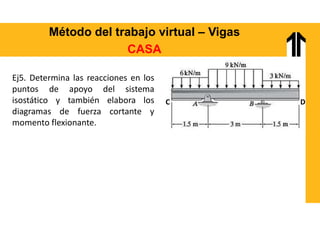
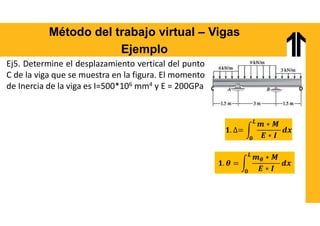
El documento aborda el análisis estructural mediante el método del trabajo virtual, aplicable a armaduras y vigas en el diseño de estructuras. Se presentan objetivos de aprendizaje para resolver sistemas hiperestáticos, temas a cubrir e implementaciones prácticas relacionadas con cálculos de desplazamientos y reacciones en estructuras. Además, incluye ejemplos y ejercicios para ilustrar conceptos clave en el diseño conforme a normas vigentes.

1. Empezamos
en
un momento

2. UPN, PASIÓN POR
TRANSFORMAR VIDAS
Eduar.rodriguez@UPN. PE

3. ANÁLISIS ESTRUCTURAL
SEM3: Método del trabajo virtual o
método de la fuerza
Docente: Eduar Rodríguez B
eduar.rodriguez@upn.pe

4. T2
T1
EVALUACIÓN
X
SEM1 – PC1
X
SEM2 – PC2
X
SEM3 – PC3
X
SEM4 – PC4
X
SEM5 – PC5
X
SEM6 – PC6
X
TRABAJO FINAL
X
X
Participaciones en clase
X
X
Participaciones en los TG
X
X
Asistencia
X
X
Examen escrito
EF=100%
SEM
EVALUACIÓN
5
T1 (Examen escrito)
7
T2 (Examen escrito)
8
EF (Examen escrito)
9
ES (Examen escrito)
Trabajo final= Carátula + dedicatoria +
agradecimientos + índice + PC1, PC2…., PC6
(conclusiones en cada PC)
Trabajo individual

5. Logro de la unidad.
Al finalizar la unidad, el estudiante resuelve
sistemas hiperestáticos mediante el método de
flexibilidad para solucionar, aplicable a diseño
de estructuras en general, en concordancia
con las normas y criterios vigentes de diseño.

6. Logro de la sesión.
Al finalizar la sesión, el estudiante resuelve
sistemas hiperestáticos mediante el método
de fuerzas virtuales en armaduras y vigas,
aplicable a diseño de estructuras en
general, en concordancia con las normas y
criterios vigentes de diseño.

7. TEMAS
• Teoremas energéticos - Parte 2
• Trabajo mínimo. Carga unitaria.
• Ejemplos de aplicación.
• Descripción del Método. Convención de Signos. Elección de
redundantes.
• Estructura Primaria o Liberada.
• Estructura Secundaria o Complementaria.
• Ecuación de Compatibilidad.
• Solución de Estructuras Indeterminadas con una redundante.
Ejemplos de aplicación.
• Solución de Estructuras Indeterminadas con dos o más Redundantes.
• Ecuaciones de Compatibilidad.
• Ejemplos de Pórticos y Armaduras

8. INTRODUCCIÓN
Una estructura es un sistema, un conjunto de partes o componentes que se combinan en forma
ordenada para cumplir una función. Existen numerosas funciones, entre ellas:
Salvar un claro (puente vehicular o peatonal).
Encerrar un espacio (los edificios cumplen una función de albergue).
Contener un empuje (muros de contención, tanques, silos, represas).
Infraestructura vial o de transporte (pistas, intercambios viales).
Estética (monumentos).

9. Método del trabajo virtual - Armaduras planas

10. Método del trabajo virtual - Armaduras planas

11. Método del trabajo virtual - Armaduras planas
Ejm1. Determine el desplazamiento vertical de la junta C de la armadura de
acero que se muestra en la figura. El área de la sección transversal de cada
elemento es A=0.5 pulg2 y E = 29*103 ksi. Considere F1=F2= 4k

12. Método del trabajo virtual - Armaduras planas - sol
1.Calculando las reacciones
4 k 4 k
Ay=4 k Dy=4 k
2.Calculando las fuerzas reales
LONGITUD: L (pies)
FUERZA: N (k)
ELEMENTO
10
4
AB
10
4
BC
10
4
CD
14.14
-5.66
DE
10
-4
FE
14.14
0
FC
10
4
BF
14.14
-5.66
AF
10
4
CE

13. Método del trabajo virtual - Armaduras planas - sol
3.Calculando las reacciones para el
nuevo sistema
1 k
Ay=0.333 k Dy=0.667 k
4.Calculando las fuerzas virtuales
LONGITUD: L (pies)
FUERZA: n (k)
ELEMENTO
10
0.333
AB
10
0.33
BC
10
0.667
CD
14.14
-0.943
DE
10
-0.667
FE
14.14
0.471
FC
10
0
BF
14.14
-0.471
AF
10
1
CE
Las fuerzas virtuales en los elementos se calculan
usando el método de los nudos o secciones
aplicando una fuerza unitaria en el nodo a analizar.
(sistema inalterado)
http://engsci.stevenhe.com/trusssolver

14. Método del trabajo virtual - Armaduras planas - sol
5. Aplicando la ecuación de la carga unitaria
para calcular el desplazamiento vertical en C.
n.N.L
LONG: L
(pies)
Fuerza Real:
n (k)
Fuerza Virtual:
n
ELEM.
13.320
10
4
0.333
AB
13.200
10
4
0.33
BC
26.680
10
4
0.667
CD
75.471
14.14
-5.66
-0.943
DE
26.680
10
-4
-0.667
FE
0.000
14.14
0
0.471
EB
0.000
10
4
0
BF
37.695
14.14
-5.66
-0.471
AF
40.000
10
4
1
CE
233.046
TOTAL: ∑ 𝒏. 𝑵. 𝑳
𝒚
𝒚 𝟑
𝒚

15. Método del trabajo virtual - Armaduras planas
Tarea aula
Ej1. Determine el desplazamiento vertical de la junta C de la armadura de
acero que se muestra en la figura. El área de la sección transversal de cada
elemento es A=0.5 pulg2 y E = 29*103 ksi.
2.A k 3.D k

16. Método del trabajo virtual - Armaduras planas
Tarea LABORATORIO
Ej1. Determine el desplazamiento vertical de la junta C de la armadura de
acero que se muestra en la figura. El área de la sección transversal de cada
elemento es A=0.5 pulg2 y E = 29*103 ksi.
2.A k 3.D k

17. Ej3. Determine el desplazamiento vertical (para las fig A y B) de la junta F de
la armadura de acero que se muestra en la figura. El área de la sección
transversal de cada elemento es A=600 mm2 y E = 200 GPa
Fig A
Fig B
Método del trabajo virtual - Armaduras planas
Tarea CASA
42.A kN
12.F kN

18. Ej4. Determine el desplazamiento vertical (para las fig A y B) de la junta F de
la armadura de acero que se muestra en la figura. El área de la sección
transversal de cada elemento es A=0.5 pulg2 y E = 29*103 ksi
Método del trabajo virtual - Armaduras planas
Tarea CASA
7.F k

19. Ej4. Determine el desplazamiento vertical (para las fig A y B) de la junta F de
la armadura de acero que se muestra en la figura. El área de la sección
transversal de cada elemento es A=600 mm2 y E = 200 GPa
Método del trabajo virtual - Armaduras planas
Tarea CASA
5.G k

20. Método del trabajo virtual – Vigas
Desplazamiento
Rotación de la tangente o el
ángulo Ө de la pendiente en un
punto
𝑳
𝟎 𝜽
𝑳
𝟎

21. Método del trabajo virtual – Vigas
Procedimiento

22. Método del trabajo virtual – Vigas
Procedimiento

23. Método del trabajo virtual – Vigas
Ejemplo
Ej5. Determine el desplazamiento vertical del punto
B de la viga que se muestra en la figura. El momento
de Inercia de la viga es I=500*106 mm4 y E = 200GPa
𝑳
𝟎
𝜽
𝑳
𝟎

24. Método del trabajo virtual – Vigas
Ejemplo - sol
Ej5. Determine el desplazamiento vertical del punto
B de la viga que se muestra en la figura. El momento
de Inercia de la viga es I=500*106 mm4 y E = 200GPa
𝑳
𝟎
𝜽
𝑳
𝟎
1.Calculando el momento real

25. Método del trabajo virtual – Vigas
Ejemplo - sol
Ej5. Determine el desplazamiento vertical del punto
B de la viga que se muestra en la figura. El momento
de Inercia de la viga es I=500*106 mm4 y E = 200GPa
𝑳
𝟎
𝜽
𝑳
𝟎
2.Calculando el momento virtual

26. Método del trabajo virtual – Vigas
Ejemplo - sol
Ej5. Determine el desplazamiento vertical del punto
B de la viga que se muestra en la figura. El momento
de Inercia de la viga es I=500*106 mm4 y E = 200GPa
𝑳
𝟎
𝜽
𝑳
𝟎
3.Calculando el desplazamiento

27. Método del trabajo virtual – Vigas
CASA
Ej5. Determina las reacciones en los
puntos de apoyo del sistema
isostático y también elabora los
diagramas de fuerza cortante y
momento flexionante.
C D

28. Método del trabajo virtual – Vigas
Ejemplo
Ej5. Determine el desplazamiento vertical del punto
C de la viga que se muestra en la figura. El momento
de Inercia de la viga es I=500*106 mm4 y E = 200GPa
𝑳
𝟎
𝜽
𝑳
𝟎
C D