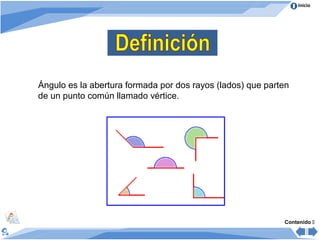
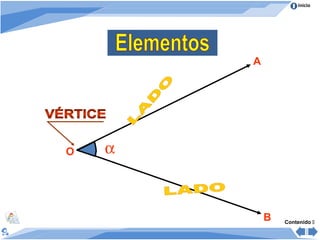
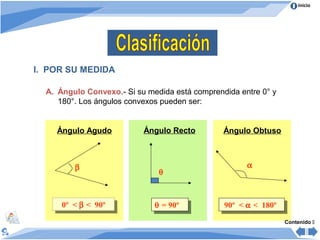
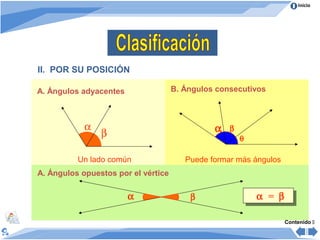
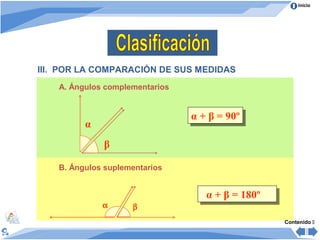
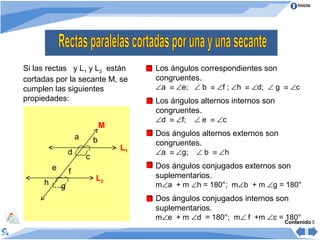
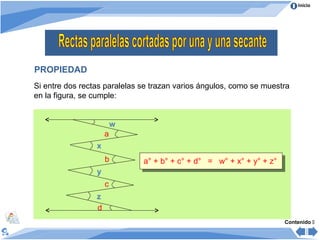
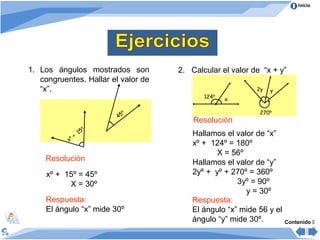
Este documento presenta información sobre ángulos. Define ángulo como la abertura formada por dos rayos que parten de un punto común llamado vértice. Clasifica los ángulos de acuerdo a su medida, posición y comparación de medidas. Explica las propiedades de ángulos formados cuando dos rectas son cortadas por una secante y cuando varios ángulos se trazan entre dos rectas paralelas. Incluye ejemplos para ilustrar los conceptos.

1. Presentación
Contenido Temático
Créditos
ÁNGULOS
Prof. CARMEN HAIDEÉ
ESTELA DÍAZ
MATEMÁTICA
1er grado de Secundaria

2. Inicio
Presentación
La geometría es una parte importante de la
cultura del hombre, no es fácil encontrar
contextos en que la geometría no aparezca
de forma directa o indirecta. Actividades tan
variadas como el deporte, la jardinería o la
arquitectura por citar algunas se sirven de la
utilización, consciente o no, de
procedimientos geométricos.
En este tema se comprenderá el concepto de
ángulos, reconoceremos los elementos y
clasificaremos los ángulos según diversos
criterios.

3. Inicio
Contenido Temático
Definición
Elementos
Clasificación
Rectas paralelas cortadas por una secante
Taller de ángulos
Ejercicios
Ejercicio interactivo
Video de ángulos

4. Inicio
Ángulo es la abertura formada por dos rayos (lados) que parten
de un punto común llamado vértice.
Contenido 

5. Inicio
A
O α
B Contenido 

6. Inicio
I. POR SU MEDIDA
A. Ángulo Convexo.- Si su medida está comprendida entre 0° y
180°. Los ángulos convexos pueden ser:
Ángulo Agudo Ángulo Recto Ángulo Obtuso
β α
θ
0º < β < 90º
0º < β < 90º θθ= 90º
= 90º 90º < α < 180º
90º < α < 180º
Contenido 

7. Inicio
I. POR SU MEDIDA
B. Ángulo Llano.- Su medida es 180°. Sus lados son 2 rayos
opuestos
θ
θ = 180º
θ = 180º
Contenido 

8. Inicio
I. POR SU MEDIDA
C. Ángulo no convexo.- Si su medida está comprendida entre 180° y
360°.
D. Ángulo de una vuelta.- Si su medida es 360°.
Teorema: La suma de las medidas de los ángulos consecutivos,
formados alrededor de un mismo vértice y en un mismo plano es
360°.
β
α
θ α + β + θ = 360°
α + β + θ = 360°
Contenido 

9. Inicio
II. POR SU POSICIÓN
A. Ángulos adyacentes B. Ángulos consecutivos
α α β
β θ
Un lado común Puede formar más ángulos
A. Ángulos opuestos por el vértice
α β α = β
α = β
Contenido 

10. Inicio
III. POR LA COMPARACIÓN DE SUS MEDIDAS
A. Ángulos complementarios
α + β = 90º
α + β = 90º
α
β
B. Ángulos suplementarios
α + β = 180º
α + β = 180º
α β
Contenido 

11. Inicio
Si las rectas y L1 y L2 están Los ángulos correspondientes son
cortadas por la secante M, se congruentes.
cumplen las siguientes ∠a ≡ ∠e; ∠ b ≡ ∠f ; ∠h ≡ ∠d; ∠ g ≡ ∠c
propiedades: Los ángulos alternos internos son
congruentes.
∠d ≡ ∠f; ∠ e ≡ ∠c
M
a Dos ángulos alternos externos son
b congruentes.
L1
d ∠a ≡ ∠g; ∠ b ≡ ∠h
c
e Dos ángulos conjugados externos son
f
L2 suplementarios.
h g m∠a + m ∠h = 180°; m∠b + m ∠g = 180°
Dos ángulos conjugados internos son
suplementarios.
m∠e + m ∠d = 180°; m∠ f +m ∠c = 180°
Contenido 

12. Inicio
PROPIEDAD
Si entre dos rectas paralelas se trazan varios ángulos, como se muestra
en la figura, se cumple:
w
a
x
b a° + b° + c° + d° = w° + x° + y° + z°
y
c
z
d
Contenido 

13. Inicio
1. Los ángulos mostrados son 2. Calcular el valor de “x + y”
congruentes. Hallar el valor de
“x”. 2y y
124º x
º 270º
45
Resolución
º
15 Hallamos el valor de “x”
+
xº
xº + 124º = 180º
X = 56º
Resolución Hallamos el valor de “y”
xº + 15º = 45º 2yº + yº + 270º = 360º
X = 30º 3yº = 90º
y = 30º
Respuesta: Respuesta:
El ángulo “x” mide 30º El ángulo “x” mide 56 y el
ángulo “y” mide 30º. Contenido 

14. Inicio
Contenido 